| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
ФРАКТАЛЫ И УНИВЕРСАЛЬНОЕ УРАВНЕНИЕ
А. М. Белов
Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Обычно эти части бесконечно уменьшаются или увеличиваются и представляют собой уменьшенную копию целого (по крайней мере, приблизительно).
С другой стороны фрактал является функцией – математическим выражением, описывающим эту структуру. Таким образом, получение нового фрактала неразрывно связано с получением соответствующего математического выражения или системы математических выражений.
С момента появления понятия "фрактал" постоянно активно ведутся поиски математических выражений способных задавать разнообразные фракталы. По этому проверка универсального уравнения на способность задавать фракталы является вполне логичной.
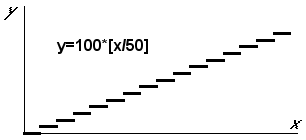
Под универсальным уравнением понимается математическое выражение вида: y=[x/a]*[a/x], где [ ] – знак, обозначающий целую часть числа (и далее по тексту статьи). Путем введения в универсальное уравнение различных добавлений и преобразований практически можно получать бесконечное количество производных уравнений, описывающих самые разнообразные объекты.
Универсальное уравнение в своем элементарном виде состоит из двух функций: [x/a] и [a/x]. Если посмотреть на приведенный ниже график подобной функции, то можно убедиться, что эти функции сами являются фракталами.

Действительно, любая часть этого графика подобна, как всему графику, так и отдельным другим его частям и размеры этих частей постепенно увеличиваются, что характерно для фракталов. Эти элементарные функции сами могут послужить основой для получения более сложных фракталов, например, приведенного ниже на рисунке:
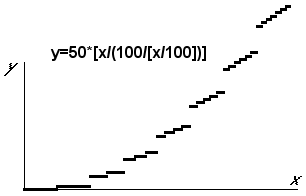
Причем, используя универсальное уравнение можно получить уравнение, задающее своеобразный фрактал – основу для получения других самых разнообразных фракталов:
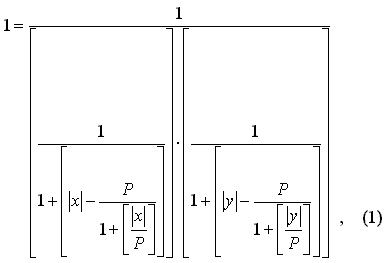
где P – число (может быть и функция), определяющее основные свойства фрактала. Фрагмент графика уравнения (1) приведен ниже:
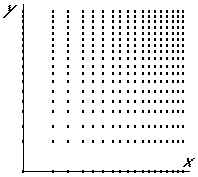
Каждая точка этого графика может служить "инициатором" для построения графика, какой либо функции, в результате чего могут получаться самые разнообразные фракталы. Например, такие, как приведенный ниже:

Таким образом, использование универсального уравнения для задания фракталов позволяет получать фракталы отличные от уже известных. Причем принципы построения фракталов на основе универсального уравнения так же отличаются от традиционно используемых. Для задания фракталов используются неявные функции и способность универсального уравнения задавать нестационарные периодические функции. Любой фрагмент фрактала можно построить, не строя и не просчитывая его предыдущие фрагменты.
Далее в качестве примеров приводится ряд фракталов, заданных с помощью универсального уравнения.
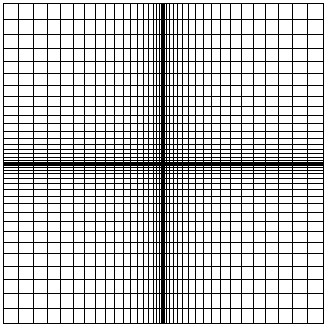
На приведенном ниже рисунке показан
фрагмент фрактала представляющий собой
проекцию на плоскость xy
графика уравнения:
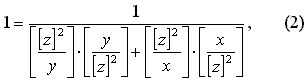
Этот же фрактал по своему интересен и в трехмерном исполнении:
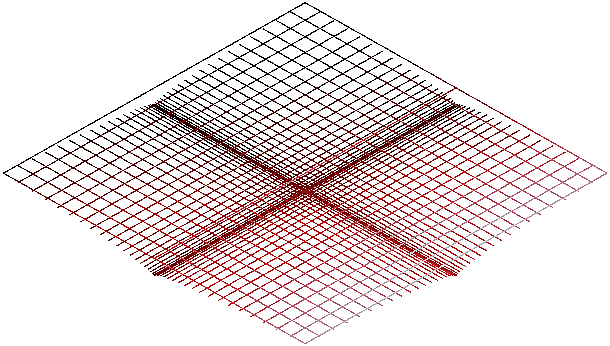
Освещение этого фрактала и других в этой статье сделано искусственно и никак не связано со способом их задания.
На приведенном ниже рисунке показан фрагмент фрактала, представляющего собой бесконечную коробку, состоящую из постоянно уменьшающихся в размерах ячеек, построенных в соответствии с формулой:
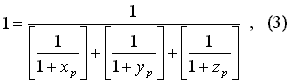

Для того, что бы лучше разобраться в "устройстве" этого фрактала можно посмотреть специальную программу построения фрактала "коробка".
На приведенном ниже рисунке показан фрагмент фрактала, представляющего собой объемную бесконечную решетку, состоящую из постоянно уменьшающихся в размерах ячеек, построенных в соответствии с формулой:
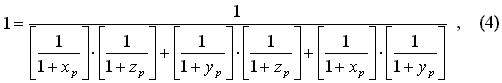
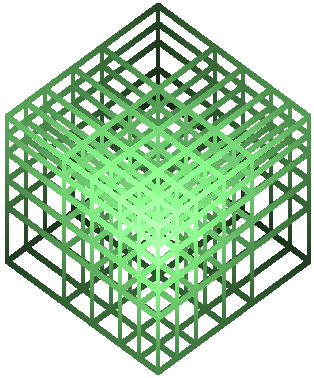
Для того, что бы лучше разобраться в "устройстве" этого фрактала можно посмотреть специальную программу построения фрактала "объемная решетка".
В уравнениях (3) и (4) вычисление параметров осуществляется по формулам:
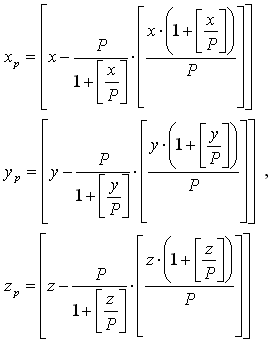
где P – число (может быть и функция), определяющее основные свойства фракталов "коробка" и "объемная решетка".
Если в функциях, заданных при помощи универсального уравнения, определяющих фракталы, случайным образом менять какие-либо параметры то можно получить стохастические фракталы. В качестве примеров таких фракталов ниже приведены фракталы "опавшие листья" и "цветы".
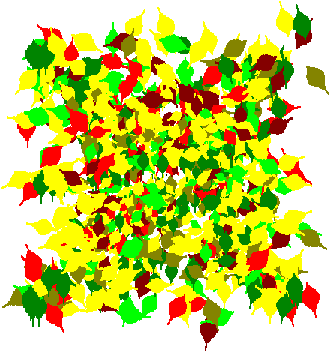
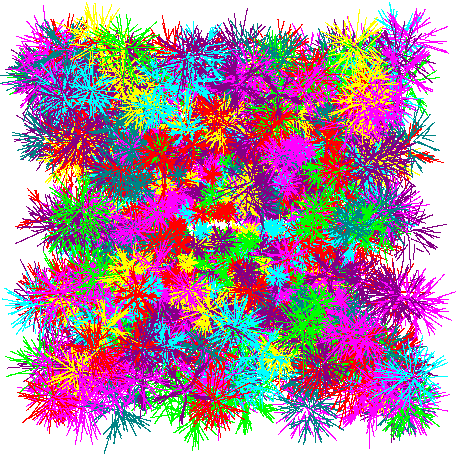
Интересно, что системы уравнений, задающие фракталы "опавшие листья" и "цветы" совсем мало отличаются друг от друга.
Понаблюдать за построением фракталов "опавшие листья" и "цветы" при изменении исходных параметров можно при помощи специальной программы.
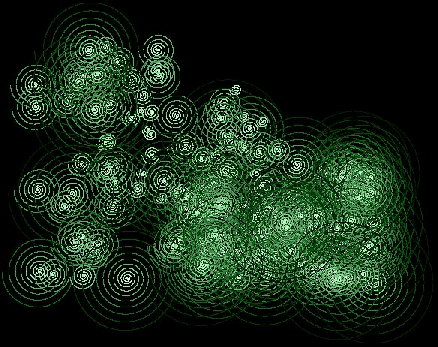
Далее приведены четыре примера стохастических фракталов полученных за счет использования уравнений спиралей и многоугольников, приведенных в статьях "Уравнения многоугольников и спиралей на их основе" и "Таблица уравнений спиралей на основе универсального уравнения".



Известно, что универсальное уравнение в своем элементарном виде на графике задает точку, а сумма этих уравнений - соответственно сумму точек. С другой стороны, если взять любой фрактал и начать бесконечно уменьшать однотипные части, его составляющие, то какими бы сложными эти части ни были, они постепенно все выродятся в точки. Таким образом, можно говорить о том, что универсальный фрактал должен графически представлять собой набор точек и может задаваться суммой универсальных уравнений. Причем суммы таких уравнений в общем случае будут бесконечными, так как при представлении какого либо объекта в виде фрактала, состоящего из точек теоретически к уже имеющимся точкам, составляющим объект можно прибавлять бесконечное число новых точек с соответствующим увеличением густоты (плотности) размещения точек в пространстве.
Наблюдать подобные фракталы на статичных рисунках бессмысленно, так как наблюдаться будет только сам объект, представляемый фракталом, а части составляющие фрактал – точки нет. Поэтому для того, что бы разобраться в том, как строятся такие "универсальные фракталы" предлагаю загрузить и выполнить специальные программы: "Пористая структура" и "Горка спичек". В результате выполнения этих программ можно будет наблюдать поточечное построение фракталов в виде своеобразной анимации. Программа "Пористая структура" построит сначала трехмерный объект "набранный" крупными точками, а затем тот же объект, но "набранный" большим количеством более мелких точек с соответствующим появлением более мелких подробностей объекта, что характерно для фракталов. Программа "Горка спичек" строит горку спичек в реалистичном виде, конечно с поправкой на отсутствие антиаллисинга. Явление аллисинга конечно не присуще универсальному уравнению, но для вывода изображений мы вынуждены использовать обычный монитор, который фактически "втискивает" с соответствующими искажениями результаты вычисления координат точек по универсальному уравнению в матрицу монитора.
При работе с программами можно так же заметить, что выполняемые на экране трехмерные построения отличаются от обычной 3D графики. Обычная 3D графика обеспечивает лишь построение поверхностей объектов, а фракталы на основе универсальных уравнений весь объем, занимаемый объектом, включая его внутренности. Это обстоятельство очень важно, если фрактал предполагается в дальнейшем использовать для выполнения с ним каких либо операций, например выполнения прочностных расчетов.
Кроме этого отображаемая при помощи программы "Горка спичек" анимация в виде фрактала вместе с программой воспроизведения анимации занимает 11,7 МБ. Это при том, что программа фактически демонстрирует в ходе построения фрактала 246720 отличных друг от друга кадров анимации. Если бы подобную анимацию создавали бы, например, в формате gif, то при среднем размере одного кадра в формате gif 9,4 кБ вся анимация заняла бы 2319 МБ или была бы больше фрактала в 198 раз.
февраль 2005 года