| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
Известно, что в современной аналитической геометрии задание произвольной пространственной линии одним уравнением (формулой) не используется. Любая пространственная линия в аналитической геометрии определяется, как пересечение двух поверхностей, которые задаются уравнениями вида Ax+By+Cz=D (для плоскости) или уравнениями более высокой степени (для произвольных поверхностей). Или пространственная линия может быть задана как решение системы двух уравнений, каждое из которых задает свою поверхность.
Считается, что пространственную линию проще и удобнее задавать параметрически при помощи параметра t, используя три уравнения: x=f(t), y=f(t), z=f(t). Для прямой они будут выглядеть примерно так: x=a+bt, y=c+dt, z=k+mt. Для более сложной по форме пространственной линии и уравнения будут более сложными.
Основной задачей аналитической геометрии является изучение геометрических фигур с помощью соотношений между координатами точек, из которых эти фигуры образованы или, иначе говоря, с помощью алгебраического уравнения, связывающего координаты каждой точки фигуры. По этому вряд ли можно считать цели аналитической геометрии полностью достигнутыми, если геометрическую фигуру удалось описать лишь системой выражений и высказываний и не удалось получить одно уравнение (формулу) полностью и адекватно описывающую геометрическую фигуру. Математика это в первую очередь особый язык. Отдельное уравнение вполне может рассматриваться, как отдельное слово. Если соответствующее уравнение отсутствует, то это все равно, как если бы в языке отсутствовало слово, обозначающее конкретный объект. Катастрофы это обстоятельство конечно не вызывает. Мы указываем (описываем) такой объект, используя несколько других существующих слов. Аналогично мы поступаем и в математике, используя системы уравнений и связанные с ними словесные высказывания. Удобно это? Ну, представьте, что в нашем языке нет слова "хлеб" и мы всякий раз вместо него произносим, что-то вроде: "пищевой продукт, выпекаемый из теста, приготовленного …".
В связи с выше изложенным, поиск уравнений способных задать произвольную пространственную линию остается все еще актуальным.
Задать произвольную пространственную линию можно на основе использования универсального уравнения ([a/x][x/a], где [ ] – знак, обозначающий целую часть числа) или включения в состав такого уравнения выражения, предусматривающего извлечение корня квадратного из выражения, которое может быть равно либо нулю, либо отрицательному числу. При этом уравнение составляется таким образом, что бы при выходе координат за пределы задаваемой пространственной линии возникала ситуация либо деления на ноль, либо извлечения корня квадратного из отрицательного числа. Интересно, что при таком подходе к составлению уравнений пространственных линий одну и ту же пространственную линию можно описать бесконечно большим количеством различных по виду уравнений. По этому ниже приведен ряд примеров таких уравнений.
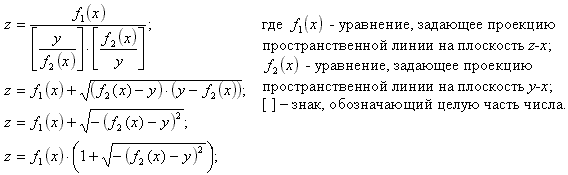
Все, приведенные примеры уравнений равноценны и могут задавать одну и ту же пространственную линию. Так же очевидно, что подобных уравнений можно составить бесконечное количество.
Ниже приведен пример конкретной пространственной линии в виде графика и уравнения, демонстрирующий возможность задания одним уравнением весьма сложных по форме пространственных линий.
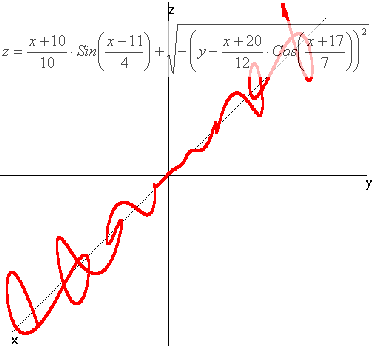
Для облегчения процедуры составления уравнений пространственных линий можно использовать специальную программу, которая автоматически формирует уравнения по заданным уравнениям проекций или составляет интерполяционное уравнение пространственной линии для заданных точек этой линии. Ниже на рисунке приведен пример выполнения трехмерной интерполяции для четырех известных точек пространственной линии. Пример приведен в виде графика линии и уравнения, задающего эту линию.
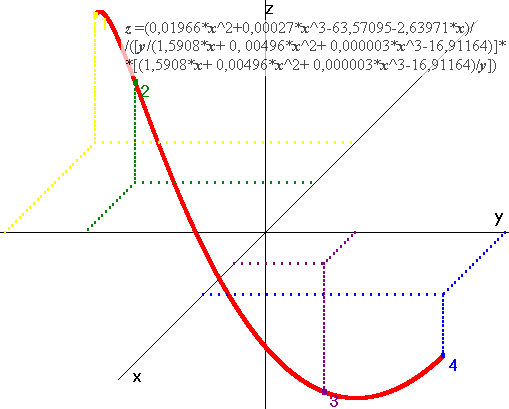
Известные до выполнения интерполяции точки пространственной линии на графике обозначены цифрами 1…4, каждая своим цветом. В приведенном на графике уравнении коэффициенты были округлены до пятого знака, а квадратные скобки предполагают выполнение операции по отбрасыванию дробной части результата получаемого в результате выполнения вычислений по выражениям, заключенным в квадратные скобки.
Использование программы позволяет без особых затруднений и трудозатрат по экспериментально определенным координатам четырех точек анализировать зависимости от двух переменных.
май 2005 года