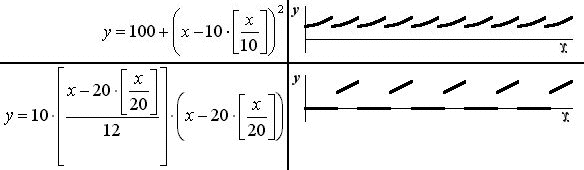
| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |

            В качестве периодической функции рассматривается функция значения, которой не изменяются при прибавлении к аргументу некоторого отличного от нуля числа. Традиционно для аналитического задания таких функций используют различные тригонометрические функции. К импульсным относят функции, претерпевающие скачкообразные изменения на множестве конечных интервалов, описывающие импульсы прямоугольной, треугольной и иной формы. Таким образом, в качестве периодической импульсной функции можно рассматривать функцию, задающую бесконечную последовательность одинаковых импульсов.

            Считается, что большинство подобных функций можно задать лишь приближенно путем аппроксимации ее тригонометрическим полиномом. Однако, если воспользоваться универсальным уравнением и его составляющими функциями, то можно получить точное задание периодических импульсных функций с импульсами самой разнообразной формы, в т. ч. с точным воспроизведением естественных импульсов, например, таких как электрокардиограмма.

            Универсальное уравнение может быть записано в следующем виде: y = [x/a][a/x], где a - число или функция, [ ] - здесь и далее по тексту статьи знак, обозначающий целую часть числа, предусматривающий выполнение операции по отбрасыванию дробной части от результата вычисления выражения, стоящего в квадратных скобках.

            О применении универсального уравнения для задания импульсных функций можно посмотреть в статье http://stob2.narod.ru/1s.htm.

            В общем виде при использовании универсального уравнения практически любая периодическая импульсная функция может быть представлена в виде:

            где d = x - p[x/p]; p - период функции.

            Ниже, в таблице, приведены примеры уравнений и их графики, составленные с использованием функции (1).

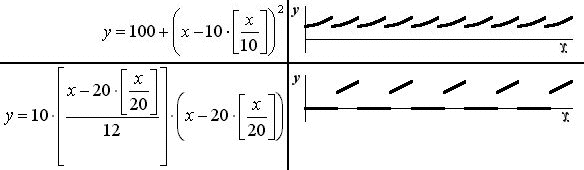
            Как можно понять, из анализа, приведенных примеров вид получаемых графиков периодических импульсных функций определяется видом функциональной связи y c d. Поскольку вид этой функциональной зависимости ни чем не ограничен и может быть любым, как и размер периода, то на основе функции (1) можно составить уравнение, задающее периодическую импульсную функцию с практически любой формой импульса.

            Так же существуют частные случаи задания периодических импульсных функций. Примеры наиболее важных из них приведены ниже в таблице:

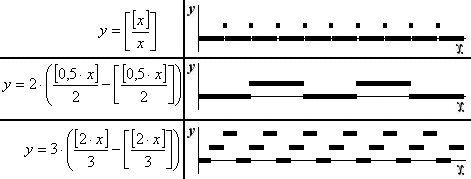
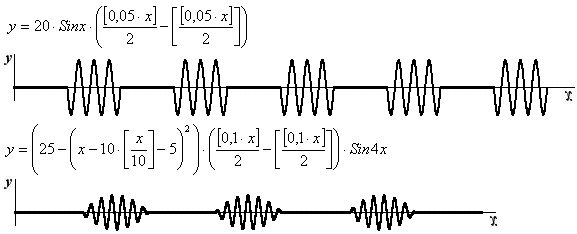
            Два последних уравнения в таблице в общем виде могут быть записаны в виде уравнения: y = l([kx]/n - [[kx]/n]), где коэффициент k определяет ширину импульса, l амплитуду импульса, а коэффициент n количество импульсов в пачке.

            Далее приведен пример (уравнение и график) периодической импульсной функции с импульсами криволинейной формы.

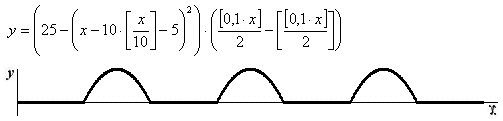
            Периодические импульсные функции, составленные на основе универсального уравнения могут использоваться совместно с иными функциями при этом можно получить описание сложных колебательных процессов в т. ч. переходных. Ниже приведены примеры (уравнения и графики), описывающие модулированные колебания или так называемые радиоимпульсы, которые были получены путем умножения периодических импульсных функций на тригонометрические функции.

            Для сравнения способов задания периодических импульсных функций при помощи универсального уравнения и путем аппроксимации тригонометрическим полиномом ниже приведены результаты задания относительно простой периодической импульсной функции, состоящей из последовательности чередующихся положительных и отрицательных единичных идеальных прямоугольных импульсов шириной 3,14 уравнением на основе универсального уравнения (первое уравнение на рис. ниже) и тригонометрическим полиномом (второе уравнение на рис. ниже). Графики этих уравнений на рисунке показаны соответственно красным и зеленым цветом.

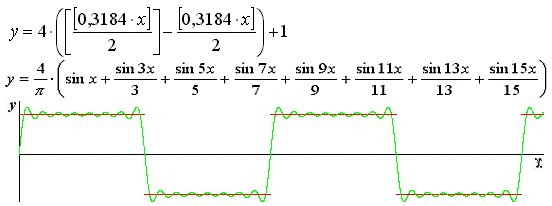
            Сравнение красного и зеленого графиков показывает, что функция, заданная при помощи универсального уравнения описывает импульсы точно без отклонений, а функция заданная тригонометрическим полиномом имеет отклонения от идеальной формы прямоугольного импульса. Причем значения функции заданной тригонометрическим полиномом в начале и конце прямоугольного импульса отличаются от идеальных фактически на сто процентов и это отклонение принципиально устранить не возможно.

            Для повышения точности воспроизведения прямоугольного импульса при помощи тригонометрического полинома необходимо значительно увеличить количество слагаемых в полиноме, а в функции, заданной при помощи универсального уравнения никаких изменений вносить не требуется.

            Необходимо отметить, что для аппроксимации тригонометрическим полиномом была выбрана периодическая импульсная функция наиболее удобная для выполнения такой аппроксимации. При аппроксимации иных периодических импульсных функций результаты могут быть гораздо хуже.

                                                                                                            ноябрь 2005 года