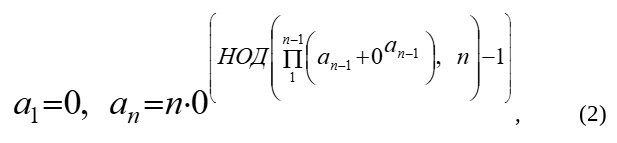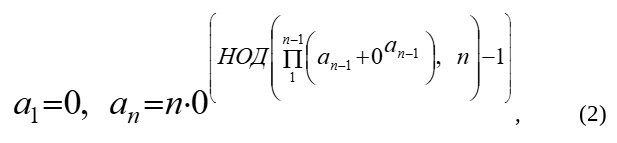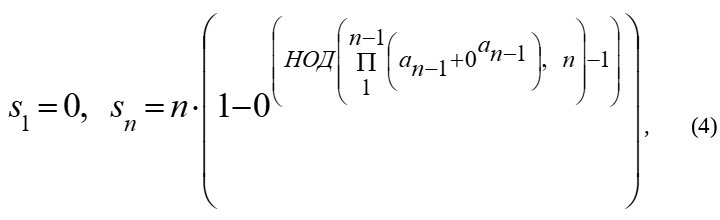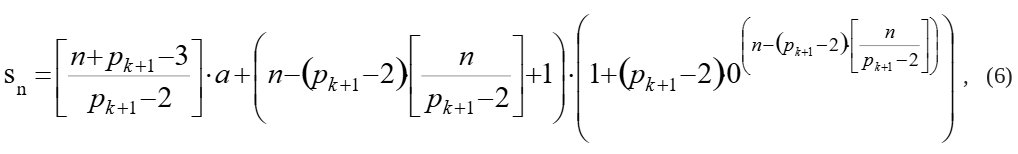| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
Формулы для вычисления членов последовательностей простых и составных чисел
А. М. Белов
По ряду причин последовательность простых чисел не удаётся задать аналитически формулой от порядкового номера её члена. Непосредственно не удалось задать последовательность простых чисел и рекуррентной формулой, которая любой член последовательности, начиная с некоторого, выражает через предшествующие члены. Поэтому в статье [1] было предложено вместо последовательности простых чисел задавать рекуррентной формулой последовательность (1).
0, 2, 3, 0, 5, 0, 7, 0, 0, 0, 11, 0, 13, 0, 0, 0, 17, 0, 19, 0, 0, 0,
23, 0, 0, 0, 0, 0, 29, 0, 31, 0, 0, 0, 0, 0, 37, 0, 0, 0, 41, 0, 43,
0, 0, 0, 47, 0, 0, 0, 0, 0, 53, 0, 0, 0, 0, 0, 59, 0, 61, 0, 0, 0, 0,
0, 67, 0, 0, 0, 71, 0, 73, 0, 0, 0, 0, 0, 79, 0, 0, 0, 83, 0, 0, 0, 0,... (1)
Числовая последовательность (1) представляет собой ряд натуральных чисел, в котором все числа, не являющиеся простыми, заменены нулями. Такая числовая последовательность легко может быть преобразована в последовательность простых чисел путём изъятия всех членов равных нулю. И при этом она может быть задана тривиальной рекуррентной формулой (2) [2].
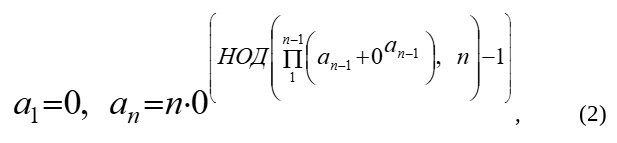
где an - значение члена последовательности (1) с порядковым номером n, n – порядковый номер членов последовательности (1), НОД – обозначение вычисления наибольшего общего делителя.
Так же, как и последовательность простых чисел не удалось формулой задать и непосредственно последовательность составных чисел. Однако вместо последовательности составных чисел можно задавать рекуррентной формулой числовую последовательность (3).
0, 0, 0, 4, 0, 6, 0, 8, 9, 10, 0, 12, 0, 14, 15, 16, 0, 18, 0, 20, 21, 22, 0, 24,
25, 26, 27, 28, 0, 30, 0, 32, 33, 34, 35, 36, 0, 38, 39, 40, 0, 42, 0, 44, 45, 46,
0, 48, 49, 50, 51, 52, 0, 54, 55, 56, 57, 58, 0, 60, 0, 62, 63, 64, 65, 66, 0, 68,
69, 70, 0, 72, 0, 74, 75, 76, 77, 78, 0, 80, 81, 82, 0, 84, 85, 86, 87, 88, ... (3)
Числовая последовательность (3) представляет собой ряд натуральных чисел, в котором все числа, не являющиеся составными, заменены нулями. Такая числовая последовательность легко может быть преобразована в последовательность составных чисел путём изъятия всех членов равных нулю. И при этом она может быть задана тривиальной рекуррентной формулой (4).
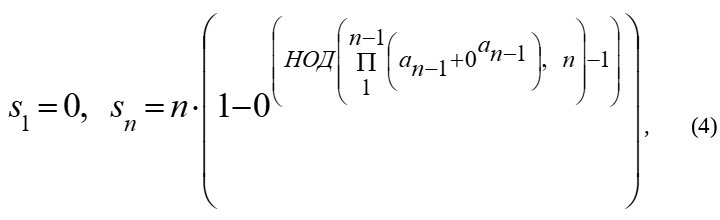
где sn - значение члена последовательности (3) с порядковым номером n, an - значение члена последовательности (1) с порядковым номером n, n – порядковый номер членов последовательности (1) и (3), НОД – обозначение вычисления наибольшего общего делителя, s1= a1=0.
Особенностью формулы (4) является то, что в ходе вычисления значений членов последовательности (3) используются значения членов последовательности (1), что обеспечивает сокращение объёма вычислений при её применении.
В формулах (2) и (4) выражение П1n-1 (an-1 + 0^an-1) фактически представляет собой произведение всех простых членов an последовательности (1) от a2 = 2 до an-1 включительно. Для данного произведения относительно недавно было введено специальное обозначение P#, получившее название праймориал, то есть произведения всех простых чисел, не превосходящих заданное простое число P.
Однако использовать праймориал в формулах (2) и (4) в целях сокращения объёма этих формул нежелательно, так как при работе с большими числами становится целесообразным применение ряда частичных произведений простых чисел, что было показано в статье [3]. Кроме этого при применении формулы (2) для вычисления всех простых чисел подряд в отдельных интервалах достаточно использовать частичные произведения всех простых членов an. Что позволяет производить вычисление простых чисел параллельно на различных вычислительных устройствах и сократить объём вычисления. Это, в свою очередь, может обеспечить возможность факторизации больших чисел.
Числовые последовательности (1) и (3) отличаются друг от друга по наличию закономерностей в распределении их членов.
Так в числовой последовательности (1) имеются только два тривиальных члена это первое чётное и нечётное числа, то есть два и три. Под тривиальными членами числовых последовательностей (1) и (3) здесь понимаются члены отличные от нуля и простоту или составность, которых можно проверить без выполнения вычислений. В то время как в числовой последовательности (3), имеется бесконечно много тривиальных членов, это все члены с чётными порядковыми номерами и все члены с порядковыми номерами больше пяти и заканчивающимися на пять. Кроме этого числовая последовательность (3) содержит между членами равными нулю бесконечно большое число сколь угодно больших интервалов состоящих только из составных чисел. В случае последовательности натуральных чисел это утверждение записывается как наличие между простыми числами сколь угодно больших интервалов состоящих только из составных чисел. Для вычисления членов последовательности составляющей такие интервалы была предложена формула: (m!+2), (m!+3), (m!+4),… (m!+ m), где m – любое натуральное число [4]. Так же существует более эффективный вариант этой формулы [5], которая может быть записана в следующем виде: P#+2, P#+3, P#+4,… P#+(Q-1), где P# - праймориал простого числа P, Q – простое число, следующее за простым числом P.
Необходимо отметить, что вычисленные по этим формулам интервалы подряд идущих составных чисел не всегда будут располагаться между простыми числами. Так, если для P5#=2*3*5=30 вычисленный интервал подряд идущих составных чисел: 32, 33, 34, 35, 36 будет располагаться между числами 31 и 37, оба которых простые, то уже для P7#=2*3*5*7=210 вычисленный интервал подряд идущих составных чисел: 212, 213, 214, 215, 216, 217, 218, 219, 220 будет располагаться между числами 211 и 221, из которых число 221=13*17 является составным.
Таким образом, можно утверждать, что существуют последовательности подряд идущих составных чисел состоящие не меньше, чем из Q-2 чисел. И эти последовательности могут состоять из сколь угодно большого числа чисел, так как последовательность простых чисел бесконечна [5]. Наименьшее число чисел в такой последовательности подряд идущих составных чисел может быть только 5-2=3. Иные длины таких последовательностей так же можно предсказать, так как они могут состоять только из Q-2 чисел. И при помощи рассматриваемых формул для различных значений праймориалов P# невозможно вычислить последовательности подряд идущих составных чисел одинаковой длины.
При этом для любого значения праймориала P# число последовательностей подряд идущих составных чисел одинаковой длины будет бесконечным. Это следует из того обстоятельства, что формулу: P#+2, P#+3, P#+4,… P#+(Q-1) всегда можно записать в следующем виде: j*P#+2, j*P#+3, j*P#+4,… j*P#+(Q-1), где j последовательно принимает значения чисел натурального ряда начиная с единицы и до бесконечности. При j=1 будет получен первый интервал подряд идущих составных чисел. При j=2 и так далее будут получаться последующие интервалы, имеющие одинаковую длину с первым интервалом, и следующие друг за другом с шагом равным P#. Таким образом, совокупность этих интервалов будет составлять упорядоченную бесконечную последовательность составных чисел, которая будет являться подпоследовательностью последовательности натуральных чисел или последовательности составных чисел.
Начало такой упорядоченной числовой последовательности, с наименьшей длинной интервалов подряд идущих составных чисел, приведено ниже:
8, 9, 10, 14, 15, 16, 20, 21, 22, 26, 27, 28, 32, 33, 34, 38, 39, 40, 44, 45, 46, 50,
51, 52, 56, 57, 58, 62, 63, 64, 68, 69, 70, 74, 75, 76, 80, 81, 82, 86, 87, 88, 92,
93, 94, 98, 99, 100, 104, 105, 106, 110, 111, 112, 116, 117, 118, 122, 123, 124,
128, 129, 130, 134, 135, 136, 140, 141, 142, 146, 147, 148, 152, 153, 154, 158,
159, 160, 164, 165, 166, 170, 171, 172, 176, 177, 178, 182, 183, 184, 188, 189,
190, 194, 195, 196, 200, 201, 202, 206, 207, 208, 212, 213, 214, 218, 219, 220,
224, 225, 226, 230, 231, 232, 236, 237, 238, 242, 243, 244, 248, 249, 250, … (5)
Число последовательностей подобных последовательности (5) бесконечно, но так как все они являются упорядоченными, то все они могут быть заданы аналитически формулой (6) от порядкового номера члена.
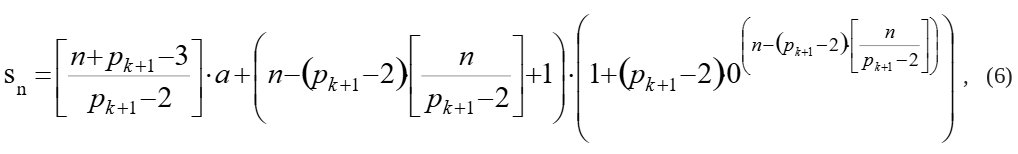
где n – порядковый номер числа sn в частичной последовательности составных чисел, [ ] – знак, обозначающий целую часть числа или обозначает операцию по отбрасыванию дробной части от результата вычисления выражения, стоящего в прямоугольных скобках (здесь и далее по тексту), a= p1*p2*…*pk, где pk простые числа, следующие в порядке их возрастания начиная с p1 = 2, k – порядковый номер простого числа в последовательности простых чисел.
Формула (6) позволяет задать числовую последовательность с бесконечным числом интервалов равной длины подряд идущих составных чисел, среди которых будет бесконечное число нетривиальных составных чисел. Например, в числовой последовательности (5) первыми такими нетривиальными составными числами будут следующие числа: 9, 21, 27, 33, 39, 51, 57, 63, 69, 81, 87, 93, 99, 111, 117, 123, 129, 141, 147, 153, 159, 171, 177, 183, 189, 201, 207, 213, 219, 231, 237, 243, 249, …
Для исследования числовых последовательностей, задаваемых формулой (6), существует специальная компьютерная «Программа вычисления членов числовой последовательности с регулярными интервалами составных чисел» [6]. Данная программа позволяет вычислить значение sn любого члена числовой последовательности с регулярными интервалами составных чисел для любых значений a и pk. Так как значения sn очень быстро растут с увеличением a и n, то программа адоптирована для работы с большими или длинными числами.
Например, уже при a=1922760350154212639070 (произведение всех простых чисел с 2 по 59) первые десять членов числовой последовательности с регулярными интервалами составных чисел выглядят следующим образом: 1922760350154212639072, 1922760350154212639073, 1922760350154212639074, 1922760350154212639075, 1922760350154212639076, 1922760350154212639077, 1922760350154212639078, 1922760350154212639079, 1922760350154212639080, 1922760350154212639081. А при n=999999999999998 sn=32589158477190272854109340330313161.
Вообще формула (6) способна возвращать сколь угодно большое нетривиальное составное число.
Кроме существования бесконечного числа интервалов равной длины подряд идущих составных чисел существуют так же и интервалы, которые могут содержать не только составные числа, но и простые числа. Эти интервалы так же имеют равную длину и бесконечно следуют друг за другом с шагом равным P#. Очевидно, что все простые числа принадлежат этим интервалам. В каждый такой интервал, состоящий не менее чем из ((j+1)*P#+1)-( j*P#+(Q-1)) чисел, входят числа натурального ряда от числа j*P#+Q по число (j+1)*P#+1. Совокупность таких интервалов составляет упорядоченную бесконечную последовательность чисел, которая будет являться подпоследовательностью последовательности натуральных чисел.
Очевидно, что наименьшая длина интервала, который может содержать простые числа, будет при P3#=2*3=6. И составит ((1+1)*6+1)-(1*6+(5-1))=3 числа.
Начало упорядоченной числовой последовательности, с наименьшей длинной интервалов подряд идущих чисел, среди которых могут быть простые числа, приведено ниже:
5, 6, 7, 11, 12, 13, 17, 18, 19, 23, 24, 25, 29, 30, 31, 35, 36, 37, 41, 42, 43, 47, 48, 49, 53, 54, 55, 59, 60, 61,
65, 66, 67, 71, 72, 73, 77, 78, 79, 83, 84, 85, 89, 90, 91, 95, 96, 97, 101, 102, 103, 107, 108, 109, 113, 114,
115, 119, 120, 121, 125, 126, 127, 131, 132, 133, 137, 138, 139, 143, 144, 145, 149, 150, 151, 155, 156, 157,
161, 162, 163, 167, 168, 169, 173, 174, 175, 179, 180, 181, 185, 186, 187, 191, 192, 193, 197, 198, 199, ... (7)
Можно так же отметить, что для получения числовых последовательностей, содержащих все простые числа и часть составных чисел, более рационально использовать системы арифметических прогрессий. Правила составления наиболее эффективных таких арифметических прогрессий были приведены в статье [2]. А для получения числовых последовательностей, содержащих все простые числа и минимальное количество составных чисел, совместно с системами арифметических прогрессий следует использовать числовые последовательности, формируемые при помощи формулы (6).
Июль 2024 года.
Литература:
1. А.М. Белов. Теория чисел: простые числа и универсальное уравнение [Электронный ресурс]. - Интернет адрес: http://stob2.narod.ru/2s.htm, 2003.
2. А.М. Белов. Задание числовых рядов и последовательностей с простыми числами и формулы простых чисел [Электронный ресурс]. - Интернет адрес: http://stob2.narod.ru/40s.htm, 2022.
3. А.М. Белов. Детерминированный тест простоты Ферма и эффективный алгоритм факторизации больших чисел [Электронный ресурс]. - Интернет адрес: http://stob2.narod.ru/41s.htm, 2022.
4. Я.И. Перельман Занимательная алгебра. – Издание одиннадцатое. – М.: Наука, 1967. – 201 с.
5. Интервалы между простыми числами [Электронный ресурс]. - Интернет адрес: https://ru.wikipedia.org/wiki/Интервалы_между_простыми_числами, 2024.
6. А.М. Белов. Программа вычисления членов числовой последовательности с регулярными интервалами составных чисел [Электронный ресурс]. - Интернет адрес: http://stob2.narod.ru/17p.htm, 2024.
Выход на главную страницу