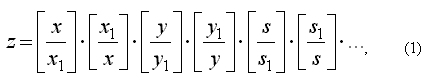
| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |

РАСПОЗНАВАНИЕ ОБРАЗОВ: МАТЕМАТИЧЕСКИЙ АППАРАТ

             Белов А.М.

             Распознавание образов предусматривает установление принадлежности некоторого объекта к одному из заранее выделенных классов объектов. Связано с разработкой теоретических основ и практической реализацией устройств, предназначенных для распознавания неизвестных объектов.

            Разработкой теории, средств и устройств распознавания образов занимается очень большое количество исследователей, и их число продолжает расти. В это направление вкладываются значительные финансовые и материальные ресурсы.

            В последние годы распознавание образов находит все большее применение. Распознавание речи, печатного и рукописного текста, различных изображений значительно упрощает взаимодействие человека с компьютером, создает предпосылки для применения различных систем искусственного интеллекта. Находит применение от геологии и медицины до военного дела. Причем в военном деле распознавание образов имеет особо большое значение. Достаточно сказать, что с распознаванием образов связаны системы наведения, системы обнаружения целей и предупреждения.

            Несмотря на большую значимость проблемы распознавания образов и вложенные в ее решение ресурсы говорить о наличии в этой области значительных успехов пока не приходится. Мы продолжаем старательно вписывать печатные буковки в прямоугольники многочисленных бланков и если вдруг не приведи господи, буковка выйдет заметно меньше или чуть больше отведенного прямоугольника, то все машина нас не поймет. А, часто мы видим  в наших больницах и поликлиниках медицинскую технику, использующую системы распознавания образов. Даже в военном деле, где средства на разработку особо экономить не принято, не наблюдается систем автоматического визуального распознавания целей в головках самонаведения или в системах предупреждения о ракетной атаке. Все перечисленное касается сравнительно простых ситуаций, требующих отличить ворону от ракеты или гражданский самолет от истребителя или рукописный шрифт, имеющий все же ограниченное количество вариантов написания. О системах же способных распознавать более сложные ситуации, например в условиях оживленного уличного движения пока можно только мечтать. Более или менее широкую распространенность получили лишь системы, работающие со стандартизированными образами такими, как печатные буквы, рукописные, но печатные буквы, написанные по образцу или работающие с ограниченным количеством образов, например такие устройства, как сканирующие отпечатки пальцев, в которых необходимо определить соответствие предъявляемого отпечатка одному единственному и в стандартных условиях сканирования.

            Сложившаяся ситуация с использованием систем распознавания образов неизбежно порождает мысль о том, что созданные в настоящее время теоретические основы работы  этих систем и в первую очередь используемый математический аппарат пока не в состоянии описать процессы, которые должны происходить при распознавании образов на достаточном для практики уровне. Если бы это утверждение было не верным, то, скорее всего, учитывая затраченные громадные усилия, мы давно бы уже имели системы распознавания любых образов.  

            Учитывая выше сказанное рассматривать теоретические основы работы систем распознавания образов, придется с самого их основания. А, что можно рассматривать в качестве такого основания ?  Очевидно, что на роль основания больше всего подходит математический аппарат, позволяющий описать любой произвольный образ. Ведь, только после получения описания образа с ним можно будет осуществлять все последующие операции для идентификации образа, да и сами эти операции зависят от способа описания образа.

            Идеально, если образ можно было бы описать одним обычным уравнением или в крайнем случае системой уравнений, но практически это удается сделать для очень ограниченного количества образов и не получается сделать в автоматическом режиме для любого произвольного образа.

            Ну, если Вы оказались привередливым, не желаете мириться с ограничениями и требуете описания действительно произвольного образа, без каких либо ограничений, то, немного покопавшись в литературе, Вы прочтете, что необходимый Вам математический аппарат существует и уже давно. Это аппарат векторной и матричной алгебры. При этом обычно утверждается, что именно при помощи этого аппарата вполне удовлетворительно описывается механизм работы зрения, особенно фасеточного глаза, например такого, как у стрекозы. Все основные вопросы с математическим аппаратом для описания произвольного образа оказывается, уже решены. Осталось немного улучшить программное обеспечение и использовать компьютер помощнее.

            Есть правда в этой картине одна небольшая дырочка. На практике все эти теоретические представления не подтверждаются. Ведь, та самая крохотная стрекоза, зрение, которой столь хорошо описывается  аппаратом векторной и матричной алгебры без каких либо     усилий летает, совершая при этом немыслимые маневры среди растительности, да еще и добычу при этом ловит, а все созданные при использовании аппарата векторной и матричной алгебры технические устройства гораздо больших размеров даже приблизительно ничего подобного повторить не могут. Тогда что же реально удается описать при помощи аппарата векторной и матричной алгебры ?  Не принимается ли в этом случае желаемое за действительное ?

            Попробуем разобраться на простом примере. Возьмем простой объект – точку и попробуем описать ее образ при помощи аппарата векторной и матричной алгебры. Для упрощения ситуации будем считать, что точка размещена в плоском пространстве. Плоскость бесконечна и по этому разобьем вокруг нашей точки только часть ее на места, в которых может находиться точка. Иначе говоря, создадим матрицу. Для начала выберем таких мест 9 и пронумеруем их по строкам от 1 до 9. Тогда образ нашей точки можно описать при помощи булевого вектора с девятью компонентами, нумеруемые по строкам: {000010000}. Если же вместо 9 мест будет использовано 25, то вектор, описывающий нашу точку, будет выглядеть уже иначе: {0000000000001000000000000}.  Теперь возьмем и уменьшим площадь одного "места" в нашей матрице в девять раз по сравнению с площадью нашей точки и тогда, при условии, что точка по форме квадратная, вектор ее, описывающий, можно будет записать в виде: {0000001110011100111000000}.  А, теперь уже не трудно догадаться, что нашу одну единственную и неизменную точку при использовании аппарата векторной и матричной алгебры можно описать бесконечно большим количеством различных векторов. Само описание нашей точки зависит не только от свойств ее самой, но и от свойств матрицы, при помощи которой она описывается. Таким образом, получается, что образ нашей точки однозначно не определен.

            Можно отказаться от булевых векторов, выбрать систему отсчета (координаты), установить системы отсчета для других свойств, например таких, как цвет точки и сформировать из этих параметров соответствующий вектор, но сложившуюся ситуацию в целом это не изменит. Свойства выбранной матрицы все равно будут оказывать решающие влияние на вид описания образа. Необходимо так же учитывать, что для совершения последующих операций с полученными матрицами они должны иметь сопоставимыми свои соответствующие параметры.

            Ясно, что от такого неоднозначного описания ничего хорошего ждать не приходится. Так почему же не удалось получить одно единственное уникальное описание  образа нашей точки, определяемое исключительно только ее свойствами ?

            По всей видимости, это связано с тем, что, используя аппарат векторной и матричной алгебры, мы описали не только образ точки, но еще и "фон" (всю площадь матрицы). Причем если мы хотим получить описания сопоставимые друг с другом, как бы мы не старались, оторвать образ точки от "фона" не удастся, так как это связано с коренными свойствами аппарата векторной и матричной алгебры. А, вот стрекоза, по всей видимости, все же умеет отрывать образ от "фона" и "описывать" их раздельно.

            Аппарат векторной и матричной алгебры рассматривался в качестве основного математического аппарата описания различных образов потому, что он способен описывать произвольную точку и соответственно любую сумму точек в пределах выбранной матрицы. Однако, для целей распознавания образов, необходим математический аппарат, способный описывать произвольную точку и произвольную сумму таких точек не в матрице, а в произвольном пространстве. Для достижения этой цели можно предложить использовать уравнение (1).

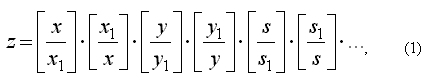
 где x, y, s,… - измерения пространства, в котором определяется точка, теоретически количество измерений ничем не ограничено; x₁,  y_1, s_{1, …} - значения параметров, определяющих в пространстве конкретную точку; [ ] – знак, обозначающий целую часть числа.

            Для всех  x, y, s,… больших нуля и при условии, что выполняются все равенства:  x=x₁, y= y_1,  s=s_{1, …}  z будет равно единице, а в противном случае будет принимать значение равное нулю. Если необходимо, что бы z могло принимать одно единственное значение, равное единице при выполнении выше, приведенных условий, то уравнение (1) необходимо переписать в виде уравнения (2). В этом уравнении при не выполнении хотя бы одного из равенств:  x=x₁, y= y_1,  s=s_{1, …} будет возникать ситуация деления на ноль.

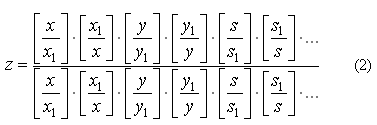
             Необходимо обратить внимание на то, что производить сокращения в уравнении (2) нельзя, что связано с возможностью возникновения ситуации деления на ноль. Так, выражение: x/x можно заменить единицей для всех значений x кроме значения x равного нулю. Таким образом, если в ходе вычислений по выражению x/x возможна ситуация, когда  x будет принимать значение равное нулю, то для избежания ошибок заменять  выражение x/x на единицу нельзя. Аналогичную ситуацию мы имеем и с уравнением (2).

Сумма уравнений вида (1) или (2) способна описывать произвольную сумму точек в произвольном пространстве.

            Используя уравнения вида (1) или (2) можно описывать любой образ без учета "фона" и формирования матрицы. Уравнения легко преобразуются при изменении системы отсчета, их вид зависит исключительно от свойств описываемого образа. Объем каждого из двух сравниваемых уравнений может быть любым и различие их объемов не влияет на процедуру сравнения.

            Для проверки принципиальной возможности использования уравнений вида (1 и 2) при описании различных образов и последующего их распознавания (сравнения) была написана специальная программа, позволяющая распознавать цифры от 0 до 9, рисуемые на мониторе при помощи компьютерной мыши. Демонстрационную версию программы можно посмотреть на http://stob2.narod.ru/program/raspoz.htm. Схема работы программы приведена на рис. 1.

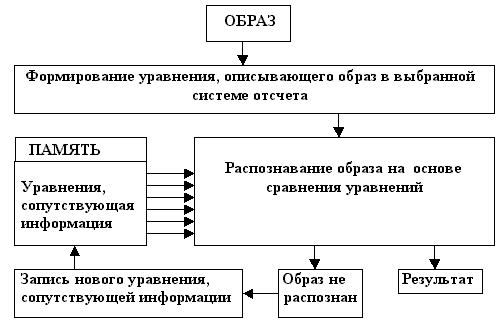
Рис.1 Схема работы программы распознавания образов

             При реализации программы не было реализовано, показанное на схеме параллельное сравнение уравнений из памяти с уравнением образа. Это сравнение осуществлялось последовательно, что предопределило большие затраты времени на процедуру распознавания. К сожалению, на это пришлось пойти из-за отсутствия компьютера способного обеспечить необходимую параллельность работы.

            О, имеющихся биологических предпосылках использования уравнений (1 и 2), а также предложенной схемы работы программы распознавания образов можно прочесть в статье "А, робот должен видеть сны?" на http://stob2.narod.ru/A_robot/a_robot.htm.

            Образцы цифр, предъявляемых программе для распознавания и успешно ею распознанные, приведены на рис. 2. Все цифры имели произвольный размер и произвольное место своего расположения на экране.

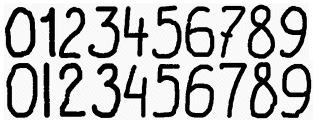
 Рис.2 Образцы цифр

            Всего во время тестирования программы ей на распознавание было предъявлено 2200 цифр или по 220 раз каждой из цифр.

            В процессе тестирования программы количество эталонных образов в ее памяти изменялось от 25 до 46. На рис. 3 показан график изменения вероятности Р правильного распознавания цифр в зависимости от изменения, количества N содержащихся в памяти эталонных образов. 

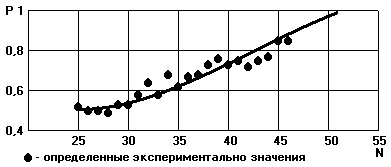
 Рис.3 Изменение вероятности правильного распознавания

                                             цифр в зависимости от количества, содержащихся  в

                                             памяти эталонных образов

             График, приведенный на рис. 3 показывает, что к 100% правильного распознавания цифр можно приблизиться уже при хранении в памяти 50-55 эталонных образов. Конечно, этот результат необходимо скорректировать с учетом того, что эталонные образы имели преимущественно вертикальную ориентацию, т. е. для распознавания цифр другой ориентации потребуются дополнительные эталонные образы и эталонные образы выполнялись одним человеком, т. е. для учета большего количества вариантов написания цифр тоже потребуется большее количество эталонных образов. Однако даже с учетом этих поправок можно говорить о том, что с использованием уравнений (1 и 2) можно практически создать работоспособную распознающую систему, содержащую разумное, с точки зрения возможности выполнения обучения, количество эталонных образов.

            В ходе тестирования программы было установлено, что вероятность правильного распознавания цифры зависит от ее вида, что показано на приведенной ниже диаграмме:

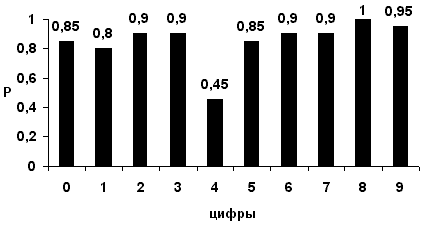
 Рис. 4 Диаграмма изменения вероятности правильного

                                                распознавания цифры в зависимости от ее вида

            Особенно плохо распознается цифра "4", что, как можно предположить, связано с большим, чем у других цифр количеством возможных вариантов ее написания.

            При тестировании программы была установлена принципиальная возможность работы программы с искаженными и комбинированными образами. Образцы успешно распознанных программой таких образов приведены на рис. 5.

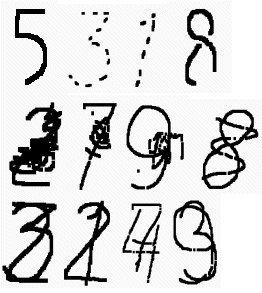
 Рис. 5 Образцы успешно распознанных искаженных

и комбинированных образов

             Верхний ряд цифр на рис. 5 показывает принципиальную возможность описывать при помощи уравнений (1 и 2)  неполные образы и успешно сравнивать их с нормальными (полными) образами. Причем в память программы были заложены только нормальные (полные) образы цифр.

            Средний ряд цифр на рис. 5 показывает принципиальную возможность выделять при помощи сравнения уравнений вида (1 и 2) образ цифры из образа зашумленного неупорядоченной информацией.

            Нижний ряд цифр на рис. 5 показывает принципиальную возможность выделять при помощи сравнения уравнений вида (1 и 2) один образ цифры из двух образов.

            Необходимо отметить, что вероятность правильного распознавания образов аналогичных приведенным на рис. 5 существенно ниже, чем образов аналогичных представленным на рис. 2. Однако и программа создавалась без учета возможности распознавания сильно искаженных образов или выделения отдельных образов из суммы других образов.

               Ссылки на дополнительные материалы: http://stob2.narod.ru/program/raspoz.htm

                                                                                          http://stob2.narod.ru/A_robot/a_robot.htm

Адрес для связи tbam1@rambler.ru   Выход на главную страницу http://stob2.narod.ru

                                                                                             май 2004 года