

В книге приведен детальный анализ формулировки знаменитой математической теоремы Пьера де Ферма и попыток ее доказательства на протяжении трех столетий с систематизацией многочисленных ошибок и заблуждений. На основе исследования личности Ферма, методов его творчества и условий его жизни вскрываются причины возобновления интереса к диофантовым уравнениям именно во Франции семнадцатого века. Рассмотрены вопросы приоритета в открытии, как Великой теоремы Ферма, так и связанной с ней теоремы Пифагора. Высказаны предположения о возможно использованных для доказательства теоремы Пьером де Ферма методах и вскрыты причины отказа от их применения в современной математике. Материал представлен на стыке математики и истории науки.
© А.М. Белов, 2016 г. - ISBN 978-3-659-79304-2
Предполагается, что примерно в 1637 году Пьер де Ферма пришел к выводу, что не может существовать трех целых чисел x, y, z, которые удовлетворяли бы уравнению xn + yn = zn, где n =3,4,5,6,7,… И тем самым фактически сформулировал самую знаменитую математическую гипотезу-головоломку, которую с учетом того, что сам Пьер де Ферма заявил о доказательстве им этой гипотезы, в последствии стали называть Великой теоремой Ферма.
Для своих современников, а как в последствии оказалось, и для потомков, Ферма оставил краткое сообщение, в котором заявлял о том, что знает решение, но умалчивал о том, в чем именно оно состоит. Несомненно, Пьер де Ферма тем самым призывал математическое сообщество попробовать повторить его достижение, решить найденную им занятную математическую головоломку.
В математике постоянно и в большом количестве ставятся различные проблемы, но уникальность проблемы Великой теоремы Ферма, заключается в том, что, несмотря на простоту ее формулировки и огромное количество предпринятых попыток решения, ответить на вызов Ферма за более чем три столетия так никто и не смог.
Время, в которое Пьер де Ферма формулировал свои теоремы, было эпохой Возрождения, началом повторного открытия древнего знания. Математики перестали заниматься своей наукой в тайне друг от друга. Они перешли к широкому общению, обсуждению проблем в своей среде. Появилось соперничество. Математики начали, как бы состязаться друг с другом, как, например, в спорте. Но если спортсмены соревновались в преодолении дистанций, поднятии тяжестей, то математики соревновались в доказательстве математических утверждений. Поэтому нет ничего удивительного в том, что Ферма был заподозрен в умышленном сокрытии им подробностей доказательства своих теорем. Ведь ему было важно не только заявить о своих достижениях, но и предложить попробовать их повторить. Возможно, именно с этим связаны некоторые странности в формулировке теоремы.
Великая теорема Ферма относится к так называемой чистой математике, ее доказательство не принесет никакой практической пользы.
Для того чтобы заниматься чистой математикой обычно требуется специальная подготовка, квалификация, как минимум, хотя бы понимание языка математики. Заниматься спортом может практически любой человек, но для достижения выдающихся спортивных результатов необходимы длительные тренировки, необходимо в совершенстве овладеть техникой выполнения упражнения. Точно также происходит и в математике, применять математические методы могут многие, но добиться выдающихся результатов особенно в чистой математике обычно могут лишь прошедшие специальную подготовку.
Однако уникальность Великой теоремы Ферма заключается также и в том, что уяснить саму проблему необычайно просто, она понятна любому школьнику. Это обстоятельство, а также объявление о премии за доказательство Великой теоремы Ферма побудило заняться решением загадки Ферма наряду с профессиональными математиками огромное количество любителей. И таких людей было столь много, что для них были введены даже специальные термины «ферматисты» или «ферматики» - люди, пытающиеся доказать теорему Ферма элементарными методами и зачастую не имеющие специального математического образования. Следствием этого явления стало рекордное количество неверных доказательств теоремы Ферма.
Постепенно среди тех, кто пытался решить проблему Ферма, то есть доказать Великую теорему Ферма, используя лишь элементарные методы, остались одни ферматисты. Но предлагаемые ими доказательства, по понятным причинам, никто серьезно не рассматривал. В результате официально было признано верным доказательство, предложенное в 1994 году Эндрю Уайлзом. Необходимо заметить, что данное доказательство не было принято всеми. Существуют, свидетельствующие об ошибочности, опубликованные замечания по доказательству Эндрю Уайлза, на которые так и не последовали ответы. Но даже если предположить, что доказательство Эндрю Уайлза все же верно, то основано оно на современных математических методах не известных во время жизни Пьера де Ферма, так что если сам Ферма и владел доказательством, то заведомо не таким.
Поэтому вопрос о наличии у Пьера де Ферма доказательства его знаменитого утверждения остался открытым. Не выяснено была ли его самая известная математическая головоломка умышленной мистификацией, розыгрышем?
Эта книга не является научным трудом по математике, и в ней не приводятся математически строгие доказательства Великой теоремы Ферма. Даны лишь предлагавшиеся в разное время общие подходы к ее доказательству в объеме достаточном для их оценки, а также подробно рассмотрена история появления теоремы и приведен, по всей видимости, наиболее полный анализ ее формулировки. Таким образом, это в первую очередь историческое исследование одной математической проблемы, а также литературное произведение о математиках, их изысканиях и о коллективном сотворении ими феномена Великой теоремы Ферма. Конечно, писать о математиках и математических проблемах и совсем не использовать специфического математического языка просто не возможно. Но из текста книги были полностью удалены все математические выражения, требующие для их понимания, знаний выходящих за пределы школьного курса математики. И кроме этого часть чисто математического материала, носящего для текста этой книги вспомогательный, справочный характер вынесено в приложения, которые могут быть пропущены при чтении книги без существенного ущерба для ее восприятия.
Впрочем, упоминать при описании одной из самых простых, совершенных и потому красивых теорем о математических понятиях, которые невозможно объяснить, как говорится, буквально на пальцах вряд ли было бы правильно.
Пьер Ферма родился 17 августа 1601 года, на юге Франции в небольшом гасконском городке Бомон-де-Ломань (Beaumont-de-Lomagne). Его отцом был зажиточный торговец, второй консул города Бомона Доминик Ферма. Должность, которую занимал отец Пьера, примерно соответствует современной должности помощник мэра. О чем свидетельствует, сохранившаяся метрическая запись от 20 августа 1601 года о крещении: «Пьер, сын Доминика Ферма, буржуа и второго консула города Бомона». Мать Пьера, Клер де Лонг, происходила из семьи юристов. В семье, кроме Пьера, были ещё один сын и две дочери.
Учитывая, что с момента рождения Пьера де Ферма прошло более четырех столетий не приходится рассчитывать узнать достоверные подробности процесса его творчества. Зато математические выражения практически с течением времени не изменяются и их исследование, в сочетании с фактами биографии ученого их сформулировавшего, может рассказать о очень многом, в том числе и о том, что было утрачено за давностью лет. Поэтому в данной книге были максимально подробно перечислены все известные факты биографии Ферма, включая даже те, которые не имели прямого отношения к его математическим исследованиям.
Доминик Ферма дал своему сыну Пьеру очень солидное образование. В колледже родного города Пьер приобрел хорошее знание языков — латинского, греческого, испанского, итальянского. Впоследствии он писал стихи на латинском, французском и испанском языках с таким изяществом, как если бы он жил во времена Августа и провел большую часть своей жизни при дворе Франции или Мадрида.
Пьер Ферма славился как тонкий знаток античности, к нему обращались за консультацией по поводу трудных мест при изданиях греческих классиков. Из древних писателей он комментировал Атенея, Полюнуса, Синезугa, Теона Смирнского и Фронтина, исправил текст Секста Эмпирика. Так что, он вполне мог бы составить себе имя в области греческой филологии. Но прославился он все же, как выдающийся математик. Хотя математика так и не стала его профессией.
Это обстоятельство было связано, прежде всего, с тем, что ученые-математики его времени обычно не имели возможности посвятить себя целиком занятиям чистой математикой. В начале XVII века математика еще только оживала после мрачного Средневековья, и занятия этой наукой в глазах общества котировались не очень высоко. Соответственно, отношение к математикам было лишено должного уважения, и многим математикам приходилось своими силами добывать средства для занятий любимой наукой. На жизнь им приходилось зарабатывать в других сферах человеческой деятельности.
К счастью Ферма обладал разносторонними способностями и мог с успехом заниматься не только математикой. В качестве своей профессии он выбирает юриспруденцию. Выбор юридического факультета в определенной степени закономерен, так как его дедушка был юристом, и вообще профессия юриста была весьма престижной. Степень бакалавра была ему присуждена в Орлеане. С 1630 года Ферма переселяется в Тулузу. В 1631 году, успешно закончив обучение, Ферма выкупил должность королевского советника парламента (другими словами, члена высшего суда) в Тулузе.
О его юридической деятельности говорится в «похвальном слове», что он выполнял ее «с большой добросовестностью и таким умением, что он славился как один из лучших юристов своего времени».
Быстрый служебный рост позволил Ферма стать членом Палаты эдиктов в городе Кастр (1648). Именно этой должности он обязан добавлением к своему имени признака знатности — частицы де; с этого времени он становится Пьером де Ферма.
Успешная карьера Ферма была связана не только с его талантами и честолюбивыми устремлениями, но и с тем, что в то время в Европе свирепствовала чума, и те, кто выживал, поднимались по служебной лестнице, занимая места умерших. Ферма тоже заболел чумой, но ему посчастливилось выжить.

Пьер де Ферма (1601 - 1665) с 1631 г. советник Тулузского парламента
и знаменитый французский математик-любитель
Таким образом, эпидемия чумы способствовала тому, что Ферма сравнительно быстро получил комфортные условия жизни. Вообще его жизнь была организована и проходила в условиях наибольшего благоприятствования раскрытию его математического таланта. Благоприятных событий за время жизни Пьера де Ферма, причем без каких либо видимых причин, случилось столь много, что в их случайность трудно поверить.
В 1631 году Пьер Ферма женился на своей дальней родственнице с материнской стороны — Луизе де Лонг. У Пьера и Луизы было пятеро детей, из которых старший, Самюэль, стал поэтом и ученым, доктором права и адвокатом. Именно им было опубликовано первое собрание сочинений Пьера де Ферма, вышедшее в 1679 году. К сожалению, Самюэль Ферма не оставил никаких воспоминаний об отце. Младший сын Клер также выбрал юридическое образование, средний, Жан, — духовную карьеру, а дочери приняли монашество.
На службе Пьер де Ферма пользовался авторитетом очень честного человека, эрудированного юриста. Интересно, что высшим чиновникам парламента предлагалось избегать излишнего общения, чтобы не давать повода для сплетен и пересудов. Вот и получилось, что Ферма вел весьма замкнутый, уединенный образ жизни, приходил со службы и садился за письменный стол. Так он работал, на одном месте, 34 года. На службе — советник следственной палаты, юрист и знаток права, неподкупный, добросовестный и честный чиновник, дома за письменным столом — великий математик. Возможно, именно вынужденный такой образ жизни в определенной мере способствовал достижению им столь впечатляющих результатов в математике.
Пьер де Ферма получил хорошее гуманитарное образование и не мог получить систематического математического образования. В его время единственное учебное заведение в Европе, где математиков активно поощряли, был Оксфордский университет, в котором Савильянскую кафедру геометрии учредили лишь в 1619 году. Живя вдали от Парижа, он был изолирован даже от того небольшого математического сообщества, которое тогда существовало во Франции. Поэтому у Ферма не могло быть наставника-учителя математики.
Считается, что наставником и учителем Ферма стала «Арифметика» Диофанта. Сочинения Диофанта (III в.) были изданы в XVI веке. Греческий текст «Арифметики» Диофанта с латинским переводом издал Клод Гаспар Баше де Мезириан в 1621 году. Один экземпляр этого перевода, опять же непонятно каким образом и почему, оказался у Пьера Ферма, и этот экземпляр, впоследствии ставший знаменитым, вызвал огромное количество толков и пересудов. Ведь никак невозможно объяснить, зачем юристу вдруг потребовалось потратить значительную сумму на приобретение такой книги. В XVII веке книги еще были редкостью и стоили очень дорого.
Пьер де Ферма читал «Арифметику» Диофанта и на полях книги делал свои замечания. Хотя нельзя полностью достоверным считать, что Ферма, как математик сформировался только лишь под влиянием «Арифметики» Диофанта.
Таким образом, по современным понятиям Пьер де Ферма, как математик был дилетантом, то есть любителем, занимающимся наукой без профессиональной специальной подготовки и поверхностно знакомый с предметом своих исследований [1]. Достоверно известно, что он действительно по математике не проходил профессиональной специальной подготовки, а вот в поверхностность его знаний о предмете исследований вряд ли можно поверить. Ведь его личный вклад в развитие математической науки впечатляет и в наше время.
Одной из первых математических работ Пьера де Ферма было восстановление двух утерянных книг Аполлония «О плоских местах». Крупную заслугу Ферма перед наукой видят, обыкновенно, во введении им бесконечно малой величины в аналитическую геометрию, подобно тому, как это, несколько ранее, было сделано Кеплером в отношении геометрии древних. Он совершил этот важный шаг в своих, относящихся к 1629 году, работах о наибольших и наименьших величинах, — работах, открывших собою тот ряд исследований Ферма, который является одним из самых крупных звеньев в истории развития не только высшего анализа вообще, но и анализа бесконечно малых в частности.
Метод Пьера де Ферма нахождения наибольших и наименьших величин состоял в следующем.
В выражение, переходящее в свое наибольшее или наименьшее значение, вместо неизвестного х вставляется сумма двух неизвестных х+е. Полученная через эту подстановку новая форма выражения приравнивается его первоначальной форме, чем и порождается взгляд на неизвестное е, как на величину крайне малую. В найденном, таким образом, уравнении опускаются содержащиеся в обеих его частях одинаковые члены, оставшиеся делятся на е и те из них, в которых е удержалось и после деления, опускаются совсем. В результате получается уравнение, доставляющее наибольшее или наименьшее значение неизвестного х.
В конце двадцатых годов Пьер де Ферма открыл методы нахождения экстремумов и касательных, которые, с современной точки зрения, сводятся к отысканию производной. В 1636 году законченное изложение метода было передано Мерсенну (о личности этого человека будет сказано позже), и с ним могли познакомиться все желающие.
В 1637—1638 годах по поводу «Метода отыскания максимумов и минимумов» у Ферма возникла бурная полемика с Декартом. Последний не понял метода и подверг его резкой и несправедливой критике. В одном из писем Декарт утверждал даже, что метод Ферма «содержит в себе паралогизм». В июне 1638 года Ферма послал Мерсенну для пересылки Декарту новое, более подробное изложение своего метода. Письмо его сдержанно, но не без внутренней иронии. Он пишет: «Таким образом, обнаруживается, что, либо я плохо объяснил, либо г. Декарт плохо понял мое латинское сочинение. Я все же пошлю ему то, что уже написал, и он, несомненно, найдет там вещи, которые помогут ему отказаться от мнения, будто я нашел этот метод случайно и его подлинные основания мне неизвестны». Пьер ни разу не изменяет своему спокойному тону. Он чувствует свое глубокое превосходство как математика, поэтому не входит в мелочную полемику, а терпеливо старается растолковать свой метод, как это сделал бы учитель ученику. Такое поведение совершенно не характерно для дилетанта – любителя.
До Ферма, систематические методы вычисления площадей разработал итальянский ученый Кавальери. Но уже в 1642 году Ферма открыл метод вычисления площадей, ограниченных любыми «параболами» и любыми «гиперболами». Им было показано, что площадь неограниченной фигуры может быть конечной.
Пьер де Ферма одним из первых занялся задачей спрямления кривых, то есть вычислением длины их дуг. Он сумел свести эту задачу к вычислению некоторых площадей. Таким образом, понятие «площади» у Ферма приобретало уже весьма абстрактный характер. К определению площадей сводились задачи на спрямление кривых, вычисление сложных площадей он сводил с помощью подстановок к вычислению более простых площадей. Оставался только шаг, чтобы перейти от площади к еще более абстрактному понятию «интеграл».
Дальнейший успех методов определения «площадей», с одной стороны, и «методов касательных и экстремумов» — с другой, состоял в установлении взаимной связи этих методов. Есть указания на то, что Пьер де Ферма уже видел эту связь, знал, что «задачи на площади» и «задачи на касательные» являются взаимно обратными. Но он нигде не развил свое открытие сколько-нибудь подробно. Поэтому честь его по праву приписывается Барроу, Исааку Ньютону и Готфриду Лейбницу, которым это открытие и позволило создать дифференциальное и интегральное исчисления.
На протяжении более двух столетий принято было считать, что Исаак Ньютон открыл дифференциальное исчисление независимо от Ферма, не зная о его работах. Но в 1934 году Луис Треншар Мур обнаружил заметку, которая позволила внести в вопрос о приоритете полную ясность и воздать Ферма по заслугам. Ньютон писал, что, разрабатывая дифференциальное исчисление, он опирался на «метод построения касательных месье Ферма». С XVIII века дифференциальное исчисление использовалось для описания закона всемирного тяготения Ньютона и его законов механики, зависящих от расстояния, скорости и ускорения.
Несмотря на отсутствие доказательств (из них дошло только одно), трудно переоценить значение творчества Пьера де Ферма в области теории чисел. Ему одному удалось выделить из хаоса задач и частных вопросов, сразу же возникающих перед исследователем при изучении свойств целых чисел, основные проблемы, которые стали центральными для всей классической теории чисел. Ему же принадлежит открытие мощного общего метода для доказательства теоретико-числовых предложений — так называемого метода неопределенного или бесконечного спуска. Поэтому Ферма по праву может считаться основоположником теории чисел.
В письме к французскому математику Бернару Френиклю де Бесси от 18 октября 1640 года Пьер де Ферма высказал следующее утверждение: «Каждое простое число делит (в оригинале — «измеряет») одну из степеней любой прогрессии минус 1, для которой показатель степени является делителем данного простого числа минус 1; и после того, как была найдена первая степень, удовлетворяющая этому свойству, все числа, имеющие показатели степени, кратные показателю первой, удовлетворяют тому же свойству». В качестве примера Ферма приводит прогрессию 3, 9, 27, 81, 243, 729… и простое число 13. 13 делит 27 - 1 (показатель степени для 27 равен 3, а 3 делит 13 - 1), из чего следует, что 13 также делит 729 - 1 (показатель степени для 729 равен 6 и кратен 3). Это утверждение получило название малой теоремы Ферма. Оно является основным во всей элементарной теории чисел.
Сам Ферма оставил свою теорему без доказательства. Первым математиком, нашедшим доказательство, был Готфрид Вильгельм Лейбниц, из рукописей которого следует, что доказательство ему было известно до 1683 года. Лейбниц не знал о результате Ферма и открыл теорему независимо. Однако работа Лейбница не была опубликована, и доказательство в 1736 году обнародовал Эйлер в статье «Theorematum Quorundam ad Numeros Primos Spectantium Demonstratio».
Среди его заслуг по развитию теории чисел, конечно же, нельзя не упомянуть о знаменитой Великой теореме Ферма. Вообще среди полученных Ферма результатов встречаются различные теоремы — от фундаментальных, важных до чисто занимательных, неважных.
Так, одно из открытий Ферма касается так называемых дружественных чисел, тесно связанных с совершенными числами, так восхитившими Пифагора двумя тысячами лет раньше. Дружественными числами называются два числа, каждое из которых равно сумме делителей другого числа. Пифагорейцы совершили необычайное открытие, установив, что 220 и 284 — дружественные числа. Делителями числа 220 служат числа 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, а их сумма равна 284. С другой стороны, делителями числа 284 служат числа 1, 2, 4, 71, 142; их сумма равна 220.
Пару чисел 220 и 284 стали считать символом дружбы. Мартин Гарднер в книге «Математические новеллы» рассказывает о том, что в Средние века имели хождение талисманы с выгравированными на них числами 220 и 284, якобы способствующими укреплению любви. Один арабский нумеролог сообщает об обычае вырезать числа 220 и 284 на плодах, один из которых влюбленный съедал сам, а другой давал съесть предмету своей страсти, как своего рода математическое средство усиления любовного влечения.
Помимо 220 и 284 других дружественных чисел не было известно вплоть до 1636 года, когда Ферма обнаружил пару 17 296 и 18 416. И хотя это открытие нельзя назвать важным, Ферма стал своего рода законодателем моды на нахождение дружественных чисел. Декарт открыл третью пару (9 363 584 и 9 437 056), а Леонард Эйлер продолжил список дружественных чисел до 62-й пары.
А вот одна из самых изящных теорем Ферма — теорема о простых числах, несомненно, являлась важной. Простым называется число, которое не имеет делителей — чисел, которые делили бы его без остатка, — кроме единицы и самого числа. Например, 13 — простое число, а 14 — не простое. Ни одно число не делит 13 без остатка, а 2 и 7 делят 14. Все простые числа подразделяются на числа, представимые в виде 4n+1, и числа, представимые в виде 4n–1, где n — некоторое целое число. Так, число 13 принадлежит к первой группе (13 = 4·3 + 1), а число 19 — ко второй группе (19 = 4·5–1). Теорема Ферма о простых числах утверждает, что простые числа первой группы всегда представимы в виде суммы двух квадратов (13 = 22 + 32), в то время как простые числа второй группы никогда в виде суммы двух квадратов не представимы.
Он первым пришел к идее координат и создал аналитическую геометрию. Он занимался также задачами теории вероятностей. Известно, что рождение нового раздела математики — теории вероятностей произошло в ходе переписки Ферма с Паскалем. Ферма и Паскаль заложили основы тех правил, которым подчиняются все азартные игры и которые могут быть использованы игроками, чтобы выработать идеальную стратегию игры и стратегию заключения пари. Кроме того, обнаруженные Ферма и Паскалем законы теории вероятностей нашли приложения в целом ряде областей человеческой деятельности — от спекулятивной игры на фондовой бирже до оценивания вероятности ядерной катастрофы.
Ферма не ограничивался одной только математикой, он занимался и физикой, где ему принадлежит открытие закона распространения света в средах. Он исходил из предположения, что свет пробегает путь от какой-либо точки в одной среде до некоторой точки в другой среде в наикратчайшее время. Применив свой метод максимумов и минимумов, он нашел путь света и установил, в частности, закон преломления света. При этом Ферма высказал следующий общий принцип: «Природа всегда действует наиболее короткими путями», который можно считать предвосхищением принципа наименьшего действия Мопертюи — Эйлера.
Где и когда Пьер де Ферма получил свои познания в области математики так и остается неизвестным. И вообще для возникновения Пьера де Ферма в качестве математика мирового уровня совсем не было никаких предпосылок. В этом качестве он как бы возник из ниоткуда, как говориться, совершенно неожиданно появился на пустом и ровном месте.
Конечно, можно утверждать, что он от природы был одаренным человеком, очень талантливым. Однако, как хорошо известно, для того чтобы талант полностью раскрылся необходимо приложить немало усилий для его развития и в первую очередь необходимо серьезное обучение талантливого человека, необходимо обеспечить такого человека знаниями, полученными его предшественниками. В противном случае можно рассчитывать лишь на разовые открытия, как правило, связанные с решением какой либо конкретной практической задачи. В возможность случайного открытия целого ряда научных направлений как-то не верится. Да и случайные догадки ведь возможны при решении одношаговых задач, то есть при решении задач, в которых совершается действие и сразу достигается конечный результат, а на доказательство теорем Ферма у большого количества весьма талантливых математиков ушло от нескольких десятков до даже сотен лет. Столь долго и тяжело одношаговые теоремы не доказываются.
Еще в этой связи необходимо отметить, что в истории не раз наблюдалось, как талантливые, но не подготовленные люди самостоятельно заново открывали уже известные знания, но в случае Ферма такого не наблюдалось. Более того, сам Ферма признавал, что обладал достаточно полными знаниями о математических достижениях своих предшественников. Так в одном из последних его писем к Каркави имеются следующие строки: «Быть может, потомство будет признательно мне за то, что я показал ему, что древние не все знали, и это может проникнуть в сознание тех, которые придут после меня для передачи факела сыновьям, как говорит великий канцлер Англии, следуя чувствам которого, я добавлю: «Многие будут приходить и уходить, а наука обогащается».
Кроме этого сверх способный и неожиданный математик Пьер де Ферма появляется (рождается) и, по сути, проживает всю свою жизнь в очень правильном, как говориться, нужном месте. Казалось бы, лучшим местом для раскрытия математических талантов Ферма был бы Париж, в котором во время его жизни находились почти все видные математики Франции того времени. Но это только на первый взгляд, так как его семья вряд ли смогла бы обеспечить ему возможность занятия в Париже таких же должностей, которые он смог занять в провинции. Ему вряд ли удалось обеспечить в Париже свое быстрое продвижение по служебной лестнице, а это означало бы отсутствие комфортных условий для занятий математикой.
Но даже если бы ему удалось пробиться в Париже, то все его силы ушли бы на обеспечение выживания в условиях постоянных заговоров и интриг. Ведь во Франции XVII век был временем небезызвестного политического интригана кардинала Ришелье, который втягивал буквально всех так или иначе вовлеченных в управление государством людей в свои опасные политические игры. Так что у Ферма в Париже не было бы шансов на спокойное занятие математикой.
Кроме того, что Пьер де Ферма родился и прожил всю свою жизнь в нужном месте, он ее еще и прожил в нужное время. Действительно, живи дилетант Ферма, в современное время вряд ли он мог бы рассчитывать на внимательное отношение со стороны математического сообщества к своим идеям. Если бы он обнародовал новые теоремы, да еще и без предъявления их доказательств, то в лучшем случае на него и его высказывания никто не обратил внимания, и они дожидались бы того времени, пока заново не будут открыты профессиональными математиками, но уже без упоминания имени Пьера де Ферма, а в худшем его посчитали бы сумасшедшим. Действительно, воплотись он сейчас в теле, какого ни будь современного юриста, и попытайся предъявить доказательство своей знаменитой теоремы, и он тут же прослыл бы не заслуживающим внимания ферматистом. Ведь современные ученые сосредоточены каждый на своем узком направлении исследований, и они очень не любят тратить время на что-то еще. И уж тем более постараются избежать общения с дилетантом.
В XVII веке, хотя и по несколько иным причинам, математики тоже были замкнуты и обычно вели свои исследования в тайне не только от всего остального общества, но даже и друг от друга.
Замкнутость математиков была традицией, сохранившейся от косситов XVI века. Косситы были знатоками всевозможных вычислений. Купцы и деловые люди прибегали к их услугам для решения сложных задач, возникающих в связи с учетом товаров. Все, кто в ту пору профессионально занимался решением задач, изобретали свои собственные хитроумные методы выполнения вычислений и держали их в тайне, чтобы сохранить свою репутацию единственных в своем роде людей, способных решать задачи того или иного типа.
Но тут, как впрочем, и все в жизни Пьера де Ферма, очень своевременно возникает фигура отца Марена Мерсенна.
Отец Марен Мерсенн внес небольшой вклад в теорию чисел, и, тем не менее, в истории математики XVII века он сыграл очень важную роль. После вступления в 1611 году в орден минимов Мерсенн изучал математику, а затем преподавал этот предмет другим монахам и монахиням в монастыре ордена в Невере. Восемью годами позже Мерсенн переезжает в Париж и присоединяется к ордену Миним дель'Анносиад, неподалеку от Пале Ройяль - места, где, обычно, собирались интеллектуалы. Мерсенн встречался с парижскими математиками, но их нежелание обсуждать научные проблемы с ним и между собой опечалило его.
По прибытии в Париж отец Мерсенн вознамерился покончить с обычаем математиков проводить исследования в тайне от своих коллег и стал всячески способствовать обмену идей между математиками и поощрять использование результатов одного математика в работе другого. Отец Мерсенн добился того, что математики начали регулярно проводить встречи. Позднее его группа стала тем ядром, вокруг которого сформировалась Французская академия. Если все приглашенные на заседание отвечали отказом, то Мерсенн все же старался собрать какую-то группу, сообщая математикам содержание писем и работ, присланных ему конфиденциально.
Мерсенн много путешествовал по Франции и далеко за ее пределами, повсюду распространяя вести о последних математических открытиях. В своих странствиях он, в частности, встречался с Пьером де Ферма и смог оказать на него заметное влияние. Даже когда от поездок пришлось отказаться, Мерсенн продолжал поддерживать отношения с Ферма и другими математиками, направляя им огромное количество писем.
Таким образом, именно благодаря деятельности отца Марена Мерсенна у Ферма, как бы сейчас сказали, появилась инфраструктура для широкого распространения его идей. Необходимо отметить, что такое, благоприятное для распространения в математике идей дилетантов время длилось по историческим меркам совсем не долго, и Ферма работал именно в этот, наиболее благоприятный для него промежуток времени.
Однако по современным представлениям никакого распространения математических идей Ферма не должно было бы произойти. Ведь согласно самому распространенному мнению Пьер де Ферма занимался математикой исключительно ради собственного удовольствия и не пытался удовлетворять свое тщеславие по этому вопросу. При этом, естественно, что о его математических занятиях вообще никто и никогда ничего узнать просто не должен был бы. Но факты его биографии, почему-то, свидетельствуют как раз об обратном.
Напряженная работа в суде, которую Пьеру де Ферма пришлось выполнять, действительно не позволила ему создать подробное собрание своих сочинений. Известно, что такой фундаментальный труд он неоднократно пытался написать. Поэтому сам Пьер де Ферма успел напечатать только два свои произведения: геометрическую диссертацию «De linearum curvarum cum lineis rectis comparatione» (Тулуза, 1660), вместе с приложением к ней и анонимную статью без заглавия, вошедшую в качестве «первой части второго прибавления» в состав книги иезуита Лалувера: «Veterum Greometria promota in septem de Cycloide libris, et in duabus adjectis Appendicibus» (Тулуза, 1660).
Из переписки Пьера де Ферма при его жизни в печать проникли, кроме нескольких отрывков, письмо к Гассенди, помешенное в VI томе «Собрания сочинений» последнего (Лион, 1658), и девять писем, напечатанных английским математиком Валлисом в его издании «Commtrcium epistolicum de Quaestionibus quibusdam Mathematicis nuper habitum inter nobilissimos Viros etc.» (Оксфорд, 1658). Этих работ для Ферма оказалось, однако же, вполне достаточным для единогласного его признания современниками одним из выдающихся математиков.
Но все же наибольшую информацию о математических работах Ферма давала обширная переписка, которую он вел с другими учеными, преимущественно с Мерсеннем, Робервалем, Паскалями: Этьенном и Блезом, Декартом, Френиклем, Каркави, Пьером Гассенди, Сенье, Булльо, Дигби, Клерселье, Лалувером и Гюйгенсом.
В XVII веке, когда еще не было специальных научных журналов, переписка между учеными играла особую роль. В ней ставились задачи, сообщалось о методах их решения, обсуждались острые научные вопросы. Письма Ферма посылал либо непосредственно корреспонденту, либо в Париж Мерсенну, который размножал их и пересылал математикам, занимавшимся аналогичными вопросами. Но письма ведь почти никогда не бывают только короткими математическими мемуарами. В них проскальзывают живые чувства авторов, которые помогают воссоздать их образы, узнать об их характере и темпераменте.
Именно письма позволяют установить, что Ферма занимался мистификациями [1] в математике, то есть намеренным разыгрыванием своих современников – математиков.
Так, несмотря на настойчивые просьбы отца Мерсенна, Ферма упорно отказывался публиковать свои доказательства. Ферма получал удовлетворение от сознания того, что он может создавать новые теоремы, которые не всегда были доступны для понимания его современников - математиков и поддразнивал своих коллег, направляя им письма с формулировками последних теорем, он неизменно умалчивал о доказательствах. Ферма бросал своим современникам вызов, испытывая их способность найти недостающее доказательство.
Таким образом, выходит, что Пьер де Ферма занимался математикой не только ради собственного удовольствия и целенаправленно ставил в известность современников о своих достижениях (возможно, надеялся, что, и потомки о них тоже узнают) и тщеславие вовсе не было ему чуждо.
То, что Ферма никогда не раскрывал своих доказательств, вызывало у его коллег чувство горького разочарования. Рене Декарт называл Ферма «хвастуном», а англичанин Джон Валлис называл его «проклятым французом». К несчастью для англичан, Ферма доставляло особое удовольствие разыгрывать своих коллег из Англии. Самый известный случай проверки сообразительности английских математиков был связан с некоторыми свойствами числа 26.
Ферма заметил, что число 26 «стиснуто» между числами 25 и 27, одно из которых представляет собой квадрат (25 = 52), а другое — куб (27 = 33). Ферма занялся поиском других чисел, зажатых между квадратом и кубом, но найти ничего так и не удалось. Родилось подозрение, что число 26 единственное. После многодневных напряженных поисков Ферма удалось выстроить сложное доказательство, не оставлявшее сомнений в том, что 26 — действительно единственное число, заключенное между квадратом и кубом. Предложенная им цепочка логических доводов убедительно свидетельствовала, что ни одно другое число не обладает этим свойством.
Ферма сообщил об уникальном свойстве числа 26 математическому сообществу и бросил вызов, предложив доказать это. Ферма открыто признал, что располагает доказательством установленного им свойства. Вопрос был в том, хватит ли у других математиков сообразительности, чтобы справиться с предложенной задачей? Несмотря на простоту формулировки, решение задачи (доказательство утверждения) оказалось чрезвычайно трудным — можно сказать, недружественным по отношению к тем, кто пытался найти его, и Ферма доставляло особое удовольствие подтрунивать над английскими математиками Валлисом и Дигби, которые, в конце концов, были вынуждены признать свое поражение.
Необходимо обратить внимание на то, что Ферма разыгрывая своих современников – математиков никогда их не пытался обманывать, намеренно вводить в заблуждение, создавать у них лишь иллюзию правильности своих рассуждений. И единственный случай, в котором его можно заподозрить в намеренном введении в заблуждение, связан с его знаменитой Великой теоремой. Причем непонятно почему именно с этой теоремой он, возможно, отступил от своих правил? Ведь при жизни он рассматривал ее всего лишь в качестве случайной задачи-головоломки, не предназначавшейся для публичного обсуждения. Или он осознавал, что время для этой задачи еще не пришло? Но догадывался, что спустя годы после его смерти именно эта случайная математическая задача-головоломка, не имеющая никакого практического значения, станет величайшим его вызовом, брошенным им всему остальному миру? И он решил максимально осложнить задачу?
Пьер де Ферма умер 12 января 1665 года в городе Кастр во время выездной сессии суда. Первоначально его похоронили там же, в Кастре, но через десять лет в 1675 году его прах перенесли в семейную усыпальницу Ферма в церкви августинцев в Тулузе.
Великая теорема Ферма – самая сложная математическая проблема из оставленных им потомкам проблем не умерла вместе с ним, а напротив мистическим образом медленно, но верно становилась все более известной, захватывала все большее количество умов во всем мире. Хотя сформулирована она была всего лишь в виде короткой заметки на полях «Арифметики» Диофанта и должна бы была просто со временем затеряться.
Но к счастью, старший сын Ферма, Клемент-Самюель взял на себя тяжкий труд подготовить к опубликованию отцовские заметки и в 1670 году он издал в Тулузе книгу под названием: «Varia opera mathematica D. Petri de Fermat, Senatoris tolosani. Accesserunt selectae quaedam ejusdem Epistolae, vel ad ipsum a plerisque doctissimis viris Gallice, Latine, vel Italice, de rebus ad Mathematicis disciplinas aut Physicam pertinentibus scriptae» («Диофантова Арифметика, содержащая примечания П. де Ферма»). В нее наряду с оригинальным текстом на древнегреческом языке и латинским переводом Клода Гаспара Баше де Мезириана вошли 48 примечаний, сделанных Ферма. В том числе и знаменитое примечание: «Наоборот, невозможно разложить ни куб на два куба, ни биквадрат на два биквадрата и вообще ни в какую степень, большую квадрата, на две степени с тем же показателем. Я открыл этому поистине чудесное доказательство, но эти поля для него слишком узки», оставленное Ферма на полях рядом с задачей Диофанта о представлении данного квадрата в виде суммы двух рациональных квадратов. Таким образом, Великая теорема Ферма была впервые опубликована.
Считается, что Клемент-Самюель сознавал важность математических достижений своего отца и поэтому сам решил издать их. Встречаются даже утверждения о том, что при этом он якобы умышленно мистифицировал Великую теорему Ферма.
Однако Клемент-Самюель не отличался значительными способностями к математике, ни в каком качестве не принимал участия при жизни Ферма в его математических исследованиях и вряд ли мог иметь представление о действительной важности математического наследия своего отца и уж тем более просто не имел возможности хоть что-то мистифицировать в математике. Именно по этим причинам, скорее всего, он даже не попытался, как-то обобщить и дополнить, обработать оставшиеся от отца материалы, а опубликовал их в том виде, в котором они были оставлены Ферма.
При этом гуманитарий Клемент-Самюель скрупулезно перепечатал математические заметки отца и не потрудился оставить о нем воспоминаний. Такое его поведение выглядит довольно странно.
С другой стороны, не для себя же Пьер де Ферма несколько позже формулировки своей теоремы дописал вторую часть своего знаменитого комментария: «Я открыл этому поистине чудесное доказательство, но эти поля для него слишком узки»? Эта часть комментария явно адресована другим математикам, но при этом размещена на полях книги, предназначенной исключительно для личного пользования. Откуда Ферма мог знать, что его заметки после его смерти будут изданы и станут общедоступны?
Но если предположить, что Пьер де Ферма заранее договорился со своим сыном об издании им его математических записей, то все эти события можно объяснить.
Как все происходило на самом деле, мы уже никогда не узнаем, но в любом случае самую грандиозную мистификацию в математике все же подготовил сам Пьер де Ферма, а запустил ее его сын Клемент-Самюель.
В 1861 г. в Берлине появилась, сделанная Фридлендером, перепечатка издания, подготовленного Самюелем.
В 1896 году в Париже было издано в трех томах более полное и совершенное собрание сочинений Пьера де Ферма, под заглавием «Oeuvres de Fermat, publiees par les soins de P. Tannery et Ch. Henry».
Обычно в современной литературе процесс открытия Великой теоремы Ферма описывается следующим образом.
Пьер де Ферма изучал математику при помощи «Арифметики» Диофанта пока примерно в 1637 году при чтении второй книги «Арифметики» не наткнулся на целую серию наблюдений, задач и решений, связанных с теоремой Пифагора и пифагоровыми тройками. Его поразило разнообразие и обилие пифагорейских треугольников, и он решил попытаться развить эту замечательную теорему Пифагора.
Получается, вот так вот, просто в ходе, по существу обучения математике, была сформулирована самая известная математическая головоломка. И никто в течение нескольких тысячелетий, что была известна теорема Пифагора, до ничего подобного не додумался. Однако не следует слепо доверять всему, что пишут в книгах. Достоверно о процессе создания Великой теоремы Ферма ведь ничего не известно. Поэтому вся эта история является лишь догадкой, красивой легендой. В действительности по ряду причин, скорее, всего события развивались немного иначе.
Когда говорят о Великой теореме Ферма, то часто утверждают, что она якобы, наряду с другими ее особенностями, является самой известной математической теоремой. Однако это не так. Потому, что самой известной теоремой все же является теорема Пифагора, которая сформулирована следующим образом: «В любом прямоугольном треугольнике квадрат, построенный на гипотенузе, равен сумме квадратов, построенных на катетах», что эквивалентно уравнению: x2 + y2 = z2, в котором х и у – длины катетов прямоугольного треугольника, а z – длина гипотенузы прямоугольного треугольника. При этом пифагоровыми тройками называют комбинации из трех целых чисел х, у и z, являющихся решениями уравнения: x2 + y2 = z2. Еще Евклид доказал, что число пифагоровых троек бесконечно велико.
Большинство жителей Земли заставляют заучивать теорему Пифагора еще в школе, и она известна миллиардам людей. А вот о Великой теореме Ферма все же знает значительно меньшее число людей.
Теорема Пифагора носит его имя, несмотря на то, что китайцы и вавилоняне использовали ее на тысячу лет раньше. Это обстоятельство объясняют тем, что китайцы и вавилоняне якобы не знали, как показать, что используемое ими правило справедливо для любого прямоугольного треугольника, а Пифагор первым это доказал, то есть в современном понимании доказал теорему.
Однако достоверно не известно располагали или нет китайцы и вавилоняне доказательством этой теоремы. Но все может измениться, ведь никто не знает, что откапают археологи через десять или сто лет?
Так Бенджамин и Эрик Альтшулеры из США в 2016 году опубликовали на сайте arXiv.org информацию о том, что вавилоняне (шумеры и аккадцы) на тысячу лет раньше индийцев и греков доказали иррациональность числа, равного квадратному корню из двух.
Доказательство этого факта считается одним из крупных достижений математики Древней Греции, приписывается пифагорейцам и датируется 570-495 годами до нашей эры. Индийские математики могли на 150-200 лет раньше греков доказать иррациональность квадратных корней из 2 и 21.
Но исследование Альтшулеров показало, что жрецы Вавилона уже в 1800-1600 годах до нашей эры, то есть более чем на тысячу лет раньше греков и индийцев владели методами, позволяющими доказать иррациональность квадратного корня из двух. К своим выводам авторы пришли, рассмотрев две глиняные таблички, отображающие приближенный расчет квадратного корня из двух.
Первая табличка позволяла получить при помощи расчета диагонали квадрата значение квадратного корня из двух с точностью до шестого знака после запятой. Вторая отображала геометрический способ проверки иррациональности квадратного корня из двух, а также содержит один из геометрических способов доказательства теоремы Пифагора.
Таким образом, уже сделанные исторические открытия позволяют уверенно утверждать, что Пифагор в лучшем случае являлся лишь популяризатором теоремы, носящей его имя, а в худшем случае, по современным представлениям, был плагиатором или, проще говоря, вором. Кроме этого открытие иррациональных чисел является важнейшим шагом для формулирования и понимания Великой теоремы Ферма, как в общем случае, так и в ее частных случаях.
В любом случае с доказательством или без доказательства, но древние китайцы и вавилоняне должны были полагать, что эта теорема справедлива для любого прямоугольного треугольника, в противном случае они просто не смогли бы ее использовать. А вот понятия теоремы тогда еще не существовало и если что-то тем или иным образом устанавливалось, то в дальнейшем передавалось в качестве абсолютного знания без каких либо объяснений и тем более доказательств. Таким образом, установленные знания распространялись как бы в виде правил или можно еще сказать в виде современных аксиом. Уж такая тогда была методика проведения научных исследований. И эта методика практически исключает возможность установления наличия в древности доказательств тех или иных утверждений. Конечно, можно рассуждать о примитивности исследований древних, но, например, использование современных аксиом тоже ведь не так уж безупречно.
Аксиома или постулат — исходное положение, утверждение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое при доказательстве других ее положений, которые, в свою очередь, называются теоремами.
В Приложении 1 приведен ряд примеров современных аксиом арифметики.
На формирование системы современных аксиом потребовалось очень много времени, и они считаются важнейшим достижением математики. Но можно ли их считать действительно надежными? Для ответа на этот вопрос попытаемся найти пример, когда какая либо аксиома не выполняется в пределах объявленной ее области применения.
Нетрудно догадаться для каких чисел, прежде всего, следует проверять аксиомы на наличие в них изъянов. Конечно, для иррациональных чисел.
Иррациональное число – это вещественное число, которое не является рациональным, то есть не может быть представлено в виде дроби m/n, где m – целое число, n – натуральное число. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби. Так иррациональными числами являются: √n для любого натурального n, не являющегося точным квадратом; ех для любого рационального х неравного нулю; ln x для любого положительного рационального х неравного единице; число пи и т. п.
Всякий раз, когда подобные числа при вычислениях будут использоваться в виде непериодических десятичных дробей, будут получаться лишь приближенные результаты. Например, √2·√2 = 1,414213562373095048801688724209 · 1,414213562373095048801688724209 = 1,999999999999999999999999999998, но ведь хорошо известно, что рассматриваемое выражение точно, а не приблизительно равно двум. А тут фактически выходит, что классические дважды два могут быть и не равны четырем? Однако если рассматриваемое выражение допускает проведение сокращений, а оно допускает проведение сокращений, то его можно представить в следующем виде: √2·√2 = √2·2 = √4 = 2. И катастрофа отменяется, но она обязательно случится, если иррациональные числа будут подставляться в выражения, не допускающие проведение сокращений. Поэтому в Приложении 1 выберем аксиому, использующую математическое выражение, не допускающее сокращений. И такая аксиома есть это распределительный закон, который гласит, что для любых чисел m, n и k m· (n + k) = m·n + m·k.
Действительно левую часть: «m·(n + k)» этого математического выражения невозможно сократить без приведения ее к виду: «m·n + m·k». Это означает, что в общем виде не удастся показать справедливость этого утверждения для любых чисел.
Остается только проверить эту аксиому на конкретных числовых примерах, для чего примем, например, m = √2, n = √2 и k = √3 и подставим эти иррациональные числа в выражение m· (n + k) = m·n + m·k.
√2· (√2 + √3) = √2·√2 + √2·√3
Теперь произведем вычисления значений левой и правой частей получившегося выражения:
√2·(√2+√3)=1,414213562373095048801688724209· (1,414213562373095048801688724209 + 1,732050807568877293527446341505) = 1,414213562373095048801688724209 · 3,146264369941972342329135065714 = 4,449489742783178098197284074701
√2·√2+√2·√3=√4+√2·3=2+√6 =2 + 2,449489742783178098197284074705 = 4,449489742783178098197284074705
Да, все вычисления необходимо осуществлять с помощью самого простого и примитивного калькулятора. Использовать компьютерные программы нельзя, так как они обычно имеют встроенные алгоритмы по корректировке и округлению результатов вычислений. Причем разработчики программного обеспечения в настоящее время об этом даже не удосуживаются пользователей поставить в известность. Поэтому неудивительно, что при малых расхождениях в результатах вычислений можно прийти к неправильным выводам. А в рассматриваемом примере расхождение между полученными результатами вычисления действительно составляет очень малую величину, всего - 0,000000000000000000000000000004. Очевидно, что по мере увеличения количества учитываемых десятичных знаков величина разницы в получаемых результатах вычислений будет становиться все меньше, но самым важным является, то, что разница в получаемых результатах совсем не исчезнет никогда. А ведь, если бы левая и правая части выражения m· (n + k)= m·n + m·k действительно были бы равны друг другу, то должны были бы получаться абсолютно одинаковые результаты даже при приближенных вычислениях.
Таким образом, распределительный закон, по крайней мере, для иррациональных чисел не выполняется. И совсем не важно, что отклонение в результатах вычислений представляет собой бесконечно малую величину, так как аксиома должна выполняться на все сто процентов, а не на 99,9999999999999… процентов. Потому что в этих вопросах не бывает почти и примерно.
Приведенный контр пример заставляет сомневаться в справедливости утверждения о том, что математическое доказательство является абсолютным. Любое математическое доказательство будет вообще существовать до тех пор, пока не будут вызывать сомнения аксиомы, на которых оно было основано. А вероятность того, что при формулировании той или иной аксиомы была допущена ошибка, существует всегда. Какой бы очевидной не казалась аксиома.
А может от аксиом можно отказаться? Оказывается нельзя. Дело в том, что любое доказательство вынуждено опираться на какие-либо утверждения, и если для каждого из них требовать своих доказательств, цепочка получится бесконечной. Чтобы не уходить в бесконечность, нужно где-то эту цепочку разорвать, то есть какие-то утверждения принять без доказательств, как исходные, то есть в виде аксиом.
Таким образом, получается, что любая теорема основывается на утверждениях, которые лишь предполагаются истинными или истинность которых в настоящее время самоочевидна. Более того, в настоящее время аксиомы не считаются непреложными и неизменными: они в процессе исторического развития знания подлежат проверке, уточнению на опыте и обоснованию. И эта проблема принципиально неустранима в рамках существующей методики математических исследований.
Кроме этого используемая в настоящее время методика математических исследований практически существовала всегда, принципиально она ни чем не отличается от того, что делали в очень глубокой древности. За тысячи лет по существу удалось лишь уточнить состав аксиом, правила их использования и развить при этом понятие доказательства. Все это вообще-то называется упорядочиванием и формализацией знаний с пополнением их новыми частными разделами математической науки. Поэтому нет никаких оснований, утверждать, что теорему Пифагора открыл именно Пифагор, если знания о ней, пусть и изложенные в отличной форме, существовали до него. И нет никаких оснований, пренебрегать знаниями древних.В связи с этим возникает вопрос, а не была ли известна в том или ином виде, так называемая Великая теорема Ферма до рождения Пьера де Ферма? И действительно, в литературе упоминается персидский математик и астроном аль-Ходжанди (полное имя - Абу Махмуд Хамид ибн аль-Хизр аль-Ходжанди), уроженец Ходжента (Таджикистан), работавший в Рее (Иран), который приблизительно за 600 лет до рождения Пьера де Ферма, в десятом веке попытался доказать, что сумма двух кубических чисел не может быть кубическим числом, то есть частный случай Великой теоремы Ферма [14].
Причем не упоминается, что аль-Ходжанди сформулировал эту гипотезу, а говориться лишь о попытке доказательства уже готового утверждения. Таким образом, получается, что гипотеза была сформулирована еще раньше. Но когда, кем и в каком виде, только ли для случая показателя степени равного трем или для более общего случая пока остается неизвестным.
Однако все же сохраняется надежда, что в этот вопрос будет внесена ясность по мере дальнейшего развития истории науки. Так, например, специалист в археоастрономии Мэтью Оссендриджвер из Берлинского университета имени Гумбольдта 29 января 2016 года опубликовал в журнале Science результаты расшифровки клинописи на четырех сохранившихся древневавилонских глиняных табличках, созданных между 350 и 50 годами до нашей эры. Таблички содержат расчет положения Юпитера на небосводе. Необходимо отметить, что эта тема была особенно интересной для вавилонских ученых, так как Юпитер отождествлялся с божеством - покровителем Вавилона - Мардуком. Мардука называли судьей богов и владыкой богов, а также верили, что он обладает способностью воскрешать мертвых.
Но хаотичное движение Юпитера, положение которого постоянно меняется в зависимости от его собственной орбиты и орбиты Земли, должно было немало озадачивать древних астрономов. Объяснение этого явления требовало продвинутого математического аппарата. И древние вавилоняне использовали вполне современные техники для вычисления положения Юпитера.
Вавилоняне разработали абстрактные математические и геометрические идеи о связи между движением, положением тела в пространстве и временем — эти идеи продолжают жить в современной математике и физике. Построение кривой для соотнесения скорости и расстояния со временем начинают прослеживаться в работах ученых из Оксфорда и Парижа приблизительно с 1350 года. Уже позже на основании этих работ Исаак Ньютон разработал интегральное исчисление. Также отмечается, что некоторые работы Пьера де Ферма способствовали созданию дифференциального и интегрального исчисления, и Исаак Ньютон опирался, в том числе и на работы Ферма.
Однако оказалось, что этот метод был известен, как минимум, на полтары тысячи лет раньше в древнем Вавилоне. Более того, имеются основания полагать, что вавилонская математика была перенята другими народами, и в Средние века математикам не пришлось изобретать все заново.
Таким образом, получается, что уровень развития математики в глубокой древности был сильно недооценен. Наблюдается постепенный перенос в более раннее время сроков открытия различных законов и методов математики. Пересматривается и сделанный европейцами в Средние века вклад в развитие математики. Поэтому есть все основания предполагать, что и Великая теорема Ферма появилась вовсе не на пустом месте и, по крайней мере, в качестве гипотезы она была сформулирована задолго до Пьера де Ферма.
Но как быть с утверждениями, что уравнение Великой теоремы Ферма: xn + yn = zn, в котором n = 3, 4, 5, 6, 7, … вытекает из уравнения: x2 + y2 = z2 теоремы Пифагора? Более того, ведь утверждается, что Великая теорема Ферма была сформулирована из-за по существу случайной замены показателя степени 2 на показатель степени 3 с одновременной попыткой найти для нового уравнения аналоги пифагоровых троек.
Действительно подобные рассуждения чисто внешне выглядят очень даже логичными. Однако уравнение xn + yn = zn и уравнение x2 + y2 = z2 похожи друг на друга только внешне и больше ничего общего не имеют. Дело в том, что уравнение теоремы Пифагора и сами пифагоровы тройки, в отличие от уравнения Великой теоремы Ферма очень геометрично, имеет очень глубокую связь с геометрией вообще и с геометрией нашего пространства в частности. Эта связь наглядно показана на приведенном ниже рисунке.
Теорема Пифагора в отличие от Великой теоремы Ферма выражает конкретную взаимосвязь между математикой и природой, в частности устанавливает соотношение, которое выполняется для всех прямоугольных треугольников и, следовательно, определяет прямой угол. В свою очередь, прямой угол определяет перпендикуляр, то есть отношение вертикали к горизонтали, а, в конечном счете, отношение между тремя измерениями нашего мира. В данном случае математика через прямой угол определяет саму структуру нашего пространства. Несомненно, теорема Пифагора имеет фундаментальное значение для геометрии и носит ярко выраженный прикладной характер.
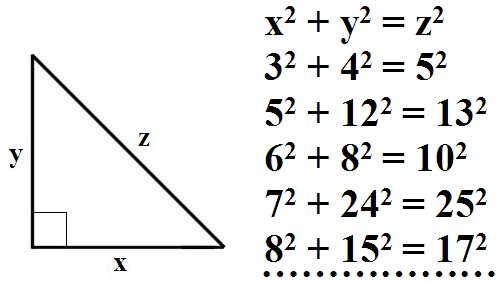
Видимо, именно с этим связано очень большое количество различных вариантов доказательства теоремы Пифагора, которых существует около четырехсот. И в подавляющем их числе использованы понятия геометрии. Пример наиболее простого такого доказательства приведен в Приложении 2.
По этому показателю Великая теорема Ферма оказалась похожа на теорему Пифагора, она также является рекордсменом по количеству предложенных доказательств, но вот только в отличие от теоремы Пифагора они все неверные.
Утверждается, что одним из толчков к нахождению целочисленных решений уравнения Великой теоремы Ферма послужили пифагоровы тройки. Однако если решения уравнения Великой теоремы Ферма являются абсолютными, то решения уравнения теоремы Пифагора из-за ее сильной связи с геометрией относительны. Вид решений уравнения теоремы Пифагора зависит от выбранной системы единиц для измерения длин сторон прямоугольного треугольника. Например, для уравнения x2 + y2 = z2, если длины сторон прямоугольного треугольника измеряются в миллиметрах: х = 3 мм, у = 4 мм, z = 5 мм при подстановке значений в уравнение получаем 32 + 42 = 52 9 + 16 = 25, а если длины сторон прямоугольного треугольника измеряются в сантиметрах: х = 0,3 см, у = 0,4 см, z = 0,5 см при подстановке значений в уравнение получаем 0,32 + 0,42 = 0,52 0,09 + 0,16 = 0,25.
Разумеется, в обоих случаях теорема Пифагора остается справедливой, но в зависимости от выбора системы единиц – миллиметры или сантиметры для одного и того же прямоугольного треугольника изменяется вид решений уравнения x2 + y2 = z2 от целых чисел до десятичных дробей.
Подобные превращения для Великой теоремы Ферма просто невозможны.
Поэтому является достаточно очевидным, что Великая теорема Ферма никак не может вытекать из теоремы Пифагора. И весьма дотошный Пьер де Ферма вряд ли мог этого не понять и не заметить.
Кроме этого известно, что Пьер де Ферма сначала на полях «Арифметики» Диофанта оставил только формулировку своей знаменитой теоремы и лишь позже ее дополнил сообщением о наличии у него доказательства теоремы. Это свидетельствует о том, что на момент формулирования своей теоремы он еще не располагал ее доказательством. А тогда на основании, каких соображений он ее сформулировал? Получается, он просто угадал, что уравнение xn + yn = zn не имеет решений в числах определенного вида?
Однако это противоречие легко устраняется, если предположить, что свои познания в математике он получал не только в «Арифметике» Диофанта, но и из других источников. И в этих источниках в том или ином виде уже была сформулирована так называемая Великая теорема Ферма. При таком развитии событий речь может идти о том, что Пьер де Ферма первоначально лишь хотел дополнить текст «Арифметики» Диофанта ставшим ему известным из других источников математическим уравнением.
Но тогда получается, что Пьер де Ферма вовсе не является автором своей Великой теоремы. Как говорится, в лучшем случае он тогда является лишь изобретателем очередного усовершенствованного велосипеда.
Да и то претендовать на существенную доработку этой теоремы он может лишь в том случае, если до него существовали формулировки только частных случаев теоремы и или если он действительно располагал первым правильным доказательством теоремы.
С другой стороны, изложенные выше факты, являются общеизвестными и, тем не менее, авторство Пьера де Ферма считается общепризнанным. Однако в этом обстоятельстве нет ничего необычного. Подобное очень часто случается в ходе развития самых разных наук. Дело в том, что общество просто привыкло считать, что изобретателем или первооткрывателем может считаться только тот, кто имеет безусловный приоритет. Понятие же приоритета стало использоваться совсем недавно и преподносилось в качестве абсолютно установленного факта первенства сделанного того или иного открытия. Но достоверно факт первенства установить даже для новых открытий пока невозможно. Не существует системы способной анализировать всю информацию, обнародованную на любых носителях и любых языках в абсолютно всех странах мира. Кроме этого с течением времени информация часто полностью или частично утрачивается. Поэтому обычно первооткрывателем признается тот, кто первым опубликовал информацию на распространенном языке в наиболее часто используемом и авторитетном издании. И даже если позже ошибка обнаруживается, то, как правило, что-то пересматривать уже бывает поздно и поэтому не принято – информация оказывается, слишком широко распространена в научной и учебной литературе. Вот в двадцать первом веке историки установили, что Пифагор вовсе не первый доказал теорему Пифагора, но практически изменить ее название уже ведь не возможно.
Примеров таких повторно сделанных открытий даже в двадцатом веке существует огромное количество. Причем часто такие открытия действительно совершались совершенно независимо. Одним из самых известных примеров является изобретение радио. Существует достаточно большое количество изобретателей радио, и в разных странах признаются изобретателями радио различные люди.
Поэтому, если уж во время компьютерной обработки информации не удается в полном объеме контролировать ее поток, то в математике Средневековья в вопросах приоритета могло происходить вообще все что угодно.
Как происходил процесс открытия Великой теоремы Ферма, независимо он ее открыл или опирался на труды предшественников, достоверно установить вряд ли уже будет возможно. Но ни у кого нет сомнений в том, что столь широкую известность эта математическая головоломка приобрела благодаря усилиям, прежде всего, Пьера де Ферма.
Сам он сформулировал свою теорему на полях «Арифметики» Диофанта напротив задачи о представлении данного квадрата в виде суммы двух рациональных квадратов в следующем виде: «Наоборот, невозможно разложить ни куб на два куба, ни биквадрат на два биквадрата и вообще ни в какую степень, большую квадрата, на две степени с тем же показателем».
В дальнейшем формулировка Ферма была приведена к современному виду: «Для любого натурального числа n > 2 уравнение xn + yn = zn не имеет решений в целых ненулевых числах x, y, z».
Также можно встретить несколько иной вариант этой формулировки: «Для любого натурального числа n > 2 уравнение xn + yn = zn не имеет решений в натуральных числах x, y, z».
Варианты отличаются тем, что в качестве решений уравнения предлагается использовать целые числа или только натуральные числа.
Натуральные числа или естественные числа — числа, возникающие естественным образом при счёте. Последовательность всех натуральных чисел 1, 2, 3, 4, 5, 6, 7, 8,…., расположенных в порядке их возрастания, называется натуральным рядом.
Множество целых чисел: …, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … - расширение множества натуральных чисел, получаемое добавлением к множеству натуральных чисел нуля и отрицательных чисел.
При анализе множеств целых и натуральных чисел становится очевидным, что если существует решение уравнения Великой теоремы Ферма для целых чисел, то существует и решение в натуральных числах. Так, пусть x, y, z – целые числа, дающие решения уравнения Великой теоремы Ферма. Если n четно, то |x|, |y|, |z| тоже будут решением, а если нечетно, то для получения натуральных решений достаточно перенести все степени отрицательных значений в другую часть уравнения, изменив знак. Поэтому обе рассматриваемые современные формулировки эквивалентны.
Правда, существует одна маленькая деталь, которая ставит под сомнение вывод об эквивалентности этих двух современных формулировок теоремы.
Как известно дьявол прячется именно в мелких деталях. И далее можно будет наблюдать, как, казалось бы, совсем несущественные детали могут привести к отличным, от принятых, выводам при рассмотрении математических утверждений.
Дело в том, что существует два подхода к определению натуральных чисел. В первом подходе натуральные числа это числа, возникающие при подсчете или нумерации предметов: первый, второй, третий и так далее. Во втором подходе натуральные числа это числа, возникающие при обозначении количества предметов: нет предметов, один предмет, два предмета, три предмета и так далее.
В первом случае ряд натуральных чисел начинается с единицы, во втором — с нуля [17]. Не существует единого для всех математиков мнения о предпочтительности первого или второго подхода или, если сказать иначе – математики до сих пор не договорились, считать ли ноль натуральным числом или нет.
Если ноль считать натуральным числом, то становится очевидным, что второй вариант современной формулировки Великой теоремы Ферма является неверным. Но видимо второй вариант современной формулировки Великой теоремы Ферма составляли приверженцы первого подхода определения натуральных чисел.
Еще необходимо обратить внимание на то, что даже если не только все математики, но и все жители Земли единогласно согласятся с тем, что ноль не является натуральным числом, эта проблема никуда не исчезнет. Так как подобное решение никогда не станет объективным. Ведь никому же в голову не приходит решать путем голосования чему равно дважды два? А в подобной заведомо неразрешимой ситуации просто необходимо в любом случае оговорить использование нуля.
При этом обе современные формулировки Великой теоремы Ферма уже совсем не эквивалентны формулировке оставленной Пьером де Ферма. Так как формулировка Ферма в отличие от современной формулировки не определяет, какие числа используются в уравнении xn + yn = zn. Тут необходимо отметить, что этот вопрос не так очевиден, как может показаться на первый взгляд.
Так, поскольку Ферма не указывает прямо, какие числа должны использоваться в качестве решений уравнения его теоремы, то в качестве решений может рассматриваться и ноль. И тогда возникает описанный выше связанный с нулем казус. И вообще в представленном Ферма виде теорема становится неверной.
Правда, игнорирование нуля в формулировке Ферма можно объяснить тем, что долгое время ноль рассматривался исключительно как математический знак, выражающий отсутствие значения данного разряда в записи числа в позиционной системе счисления. Так в Европе даже в семнадцатом веке, то есть во время жизни Ферма, ноль все еще преимущественно считался условным символом и не признавался числом.
Другое отличие формулировки Ферма и современной формулировки теоремы состоит в том, что Ферма в качестве показателя степени n предложил использовать любое число большее двух, а современная формулировка предусматривает рассмотрение лишь натуральных чисел больших двух. Непонятно зачем это было сделано?
Что изменится, если будет использован, например, показатель степени n = 2,5? Оказывается, ничего. Великая теорема Ферма останется неизменной. Это хорошо видно из следующего примера:
Например, возьмем 42,5 и, применяя элементарные правила совершения действий со степенями, преобразуем его:
42,5 = 42+0,5 = 42 · 40,5 = ((40,5)2)2 · 40,5 = (40,5)4 · (40,5)1 = (40,5)4+1 = (40,5)5 = 25
В этом выражении все конкретные числа могут быть заменены переменными и, тогда станет очевидным, что приведенные преобразования справедливы для любых чисел. То есть в качестве показателя степени n может использоваться любое вещественное число: 2,000001; 2,712; 4,9; 17,34; 79842,05712 и тому подобные. При этом любой показатель степени, выраженный через вещественное число большее двух, может быть преобразован в показатель степени в виде натурального числа также большего двух. А это уже фактически показывает справедливость Великой теоремы Ферма, как для показателей степени n в виде натуральных чисел, так и в виде вещественных чисел.
Тут необходимо отметить, что рассмотренные преобразования также показывают, что для целей доказательства Великой теоремы Ферма достаточно рассмотреть лишь случай с показателем степени n в виде натурального числа, так как полученное доказательство для натуральных чисел можно автоматически распространить и на вещественные числа.
Конечно, при таком преобразовании изменяется не только показатель степени, но и число, возводимое в степень. И существует вероятность того, что изначально натуральное число, возводимое в степень, преобразуется в вещественное число. Однако это обстоятельство также не повлияет на справедливость теоремы. Что будет показано далее.
Таким образом, можно утверждать, что теорема, заданная современной формулировкой по значению показателя степени n является частным случаем для Великой теоремы Ферма в ее изначальной формулировке.
Кроме этого необходимо отметить, что рассмотренная здесь неточность в современной формулировке Великой теоремы Ферма не является последней. Еще одна неточность связана с тем, что современная формулировка теоремы утверждает об отсутствии решений уравнения xn + yn = zn только в целых ненулевых числах x, y, z и (или) в натуральных числах x, y, z. Интересно, что сам Пьер де Ферма в своей формулировке этот вопрос формально не поясняет. Однако уравнение xn + yn = zn не имеет решений не только в натуральных и целых числах, но не имеет решений и в вещественных числах, в частности в рациональных числах (конечных дробях) [3]. Так как, если имеются решения в конечных целых числах, то обязательно будут существовать решения и в конечных дробях и наоборот.
Действительно, в соответствии с распределительным законом всегда решения для уравнения xn + yn = zn можно представить в виде выражений: x = k·d; y = k·f; z = k·g; где k – коэффициент, d, f, g – конечные числа являющиеся решениями Великой теоремы Ферма.
Теперь, если имеются целые конечные числа d, f, g, которые являются решениями уравнения xn + yn = zn, то можно всегда подобрать коэффициент k в виде дроби такой, что при умножении его на числа d, f, g будут получены конечные дроби x,y,z, которые также будут являться решениями этого уравнения. Эту же процедуру можно выполнить в обратном порядке, и перейти от конечных дробей к конечным целым числам, являющимся решениями уравнения xn + yn = zn.
Поясним эти утверждения на конкретном примере.
Возьмем числа: d = 12, f = 35, g = 37, которые являются решениями уравнения: x2 + y2 = z2 в конечных целых числах, умножим их на коэффициент k = 0,1, и получим дроби x = 1,2, y = 3,5, z = 3,7, которые будут являться решениями данного уравнения в конечных дробях.
Теперь возьмем числа: d = 1,2, f = 3,5, g = 3,7, которые являются решениями уравнения: x2 + y2 = z2 в конечных дробях, умножим их на коэффициент k = 20, и получим конечные целые числа x = 24, y = 70, z = 74, которые будут являться решениями данного уравнения в конечных целых числах.
Очевидно, что подобным образом можно преобразовать любые конечные числа, являющиеся решениями уравнения из Великой теоремы Ферма в бесконечную последовательность решений уравнения из Великой теоремы Ферма в конечных целых числах или дробях. Но это можно сделать только в том случае, если существуют решения уравнения xn + yn = zn из Великой теоремы Ферма в конечных целых числах или дробях. Так как подобных решений до сих пор обнаружено не было, то для числового примера было взято уравнение с показателем степени n = 2. Для такого уравнения конечные целочисленные решения известны. Это давно известные, так называемые, пифагоровы тройки. Тут необходимо отметить, что если бы были известны целочисленные решения для показателя степени n большего 2, то принципиально характер рассмотренных преобразований не изменился бы.
Из приведенных рассуждений также следует, что теорема, заданная современной формулировкой по виду решений x, y, z уравнения xn + yn = zn является частным случаем для Великой теоремы Ферма в ее изначальной формулировке. Ведь Пьер де Ферма в своей формулировке формально не определил вид решений x, y, z, а поэтому можно лишь предполагать, что он под ними подразумевал.
Также необходимо отметить, что поскольку Пьер де Ферма записал формулировку своей теоремы на полях «Арифметики» Диофанта напротив задачи о представлении данного квадрата в виде суммы двух рациональных квадратов, то, скорее всего, он рассматривал в качестве решений уравнения xn + yn = zn не любые числа, а только целые числа и дроби. Поскольку множество рациональных чисел является естественным обобщением множества целых чисел. Ведь любое целое число легко представляется в виде рационального числа путем деления целого числа на единицу.
Хотя, конечно, невозможно формально подтвердить, что в качестве несуществующих решений для своей теоремы Пьер де Ферма рассматривал только рациональные числа. Но все равно неясно, на каких основаниях в дальнейшем отказались от более широкой формулировки Ферма и в качестве несуществующих решений уравнения xn + yn = zn предложили использовать только целые числа. Тем более что в таком виде Великая теорема Ферма все равно является неверной в связи с тем, что существуют решения уравнения xn + yn = zn в целых и или натуральных числах [4]. Правда, для того чтобы стать такими решениями эти числа должны быть бесконечными.
Для нахождения таких решений необходимо известные решения, включающие обязательно как минимум одно иррациональное число, преобразовать в целые бесконечные числа. Это достигается путем умножения каждого члена уравнения xn + yn = zn на одно и то же число. При этом согласно распределительному закону равенство останется верным.
Очевидно, что для по членного умножения уравнения нужно подобрать такое число при умножении, на которое любой десятичной дроби, в том числе и бесконечной в результате получалось бы целое число. Здесь рассматривается десятичная дробь в связи с тем, что практически любое число, в том числе простые дроби и иррациональные числа представляются в виде десятичных конечных или бесконечных дробей.
Поскольку любая десятичная дробь может быть представлена в виде обыкновенной дроби, знаменатель которой есть целая степень числа 10, то в качестве искомого числа можно использовать число 10 возведенное в бесконечно большую степень или, иначе говоря, бесконечное произведение числа 10. Число 10 необходимо возводить именно в бесконечно большую степень в связи с тем, что бесконечная десятичная дробь заменяется обыкновенной дробью, знаменатель которой есть число 10 возведенное в бесконечно большую степень.
Для составления выражений являющихся целочисленными решениями Великой теоремы Ферма преобразуем уравнение xn + yn = zn, то есть, выразим z через x и y:
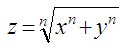
и запишем следующие формулы для вычисления целочисленных решений Великой теоремы Ферма:
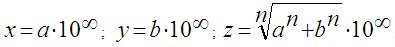
или эти же формулы можно записать иначе:
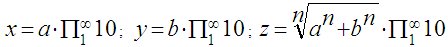
где а и b - практически любые действительные числа.
Анализ этих формул очень быстро приведет к выводу, что Великая теорема Ферма имеет бесконечно большое количество решений среди бесконечных целых чисел.
Далее приведен ряд конкретных примеров значений x, y, z, являющихся целочисленными решениями уравнения xn + yn = zn, которые были получены за счет применения выше приведенных формул. Существование лишь одного подобного примера опровергает Великую теорему Ферма, как для ее современной формулировки, так и для формулировки Пьера де Ферма.
Для n = 5:
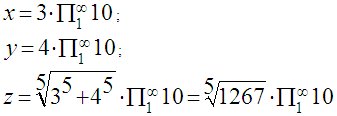
Для n = 8:
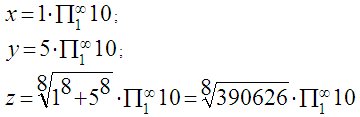
Записать, приведенные выше числа в обычном виде не представляется возможным, не хватит никакой бумаги и никаких чернил и на компьютере обработать их так же невозможно, их даже записать в компьютер не удастся, так как никакой памяти не хватит.
Поэтому для того, что бы получить хоть какое то представление о том, как эти числа выглядят в обычном виде, ниже приведены записи фрагментов этих чисел с начальной их части.
Для n=5: x=300000000…; y=400000000…; z=417402766…
Для n=8: x=100000000…; y=500000000…; z=500000159…
Казалось бы, было бы разумно ограничить используемые числа некоей их предельной величиной или длинной (общим предельным количеством используемых при записи чисел цифр). И не рассматривать необозримых монстров. Почему так нельзя поступить очень хорошо показывает гипотеза о завышенной оценке распределения простых чисел.
Продвигаясь по ряду натуральных чисел можно заметить, что найти среди них простые числа становится все труднее. Например, между 0 и 100 расположены 25 простых чисел, тогда как между 10 000 000 и 10 000 100 — только 2 простых числа. В 1791 году Карл Гаусс сформулировал приближенный закон, по которому уменьшается частота появления простых чисел. Формула Гаусса давала неплохую точность, но всегда слегка завышала истинное распределение простых чисел. Проверка на числах до триллиона показала, что гипотеза Гаусса продолжает завышать частоту появления простых чисел. И тогда посчитали, что так будет и для всех чисел до бесконечности. Так родилась гипотеза о завышенной оценке распределения простых чисел.
В 1914 году Дж. И. Литлвуд, сотрудник Г.Г. Харди по Кембриджскому университету доказал, что для очень больших чисел формула Гаусса даст заниженную оценку распределения простых чисел. А в 1955 году С. Скьюз показал, что недооценка количества простых чисел может наступить прежде, чем будет достигнуто число
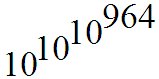
Это число невозможно даже представить, и никаких практических приложений оно не имеет. Харди назвал число Скьюза «самым большим числом, которое когда-либо служило какой-нибудь цели в математике». Но никто не доказал, что при решении различных задач не потребуется использовать еще большие числа, в том числе и бесконечные числа. То есть для адекватного решения отдельных задач необходимо предусматривать использование бесконечных чисел (чисел состоящих из бесконечного количества цифр).
Как известно и для решений уравнения xn + yn = zn не была установлена предельная величина или длина чисел, то есть решения этого уравнения следует искать среди сколь угодно больших чисел, а в пределе и среди бесконечных чисел. Формально запрет на такие решения никогда не обосновывался и не устанавливался.
При помощи ниже приведенных формул можно пронаблюдать сходимость к точному решению приведенных решений уравнения xn + yn = zn при постепенном приближении произведения числа 10 к бесконечному произведению.
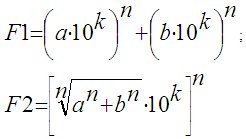
где [ ] - знак, обозначающий целую часть числа, то есть от результата вычисления выражения, заключенного в скобки [ ] необходимо отбросить дробную часть числа, а с оставшейся целой частью продолжать вычисления, k – изменяется от нуля до бесконечно большого числа, n – показатель степени в уравнении xn + yn = zn, а и b - практически любые действительные числа, которые являются соответственно решениями x и y уравнения xn + yn = zn.
При k равном бесконечно большому числу F1 будет точно равно F2, а при всех меньших значениях k F1 будет равно F2 лишь приближенно. Причем чем больше будет k, тем меньше будут отличаться F1 и F2, что демонстрирует приведенный ниже пример для случая a=2, b=3, n=3.
k=0 F1=35 F2=27 отклонение F1 от F2 22,8571… %
k=1 F1=35000 F2=32768 отклонение F1 от F2 6,3771… %
k=2 F1=35000000 F2=34965783 отклонение F1 от F2 0,0977… %
k=3 F1=35000000000 F2=34997871511 отклонение F1 от F2 0,00608… %
……………………………………………………………………………
k=∞ F1=3500000000000… F2=3500000000000… отклонение F1 от F2 0 %
Если n>2, то при помощи рассматриваемых формул можно получить одно единственное решение уравнения xn + yn = zn в целых числах для каждого значения показателя степени n и чисел a и b, а вот если n = 2 и a и b соответствуют какому либо решению уравнения xn + yn = zn в целых числах, то при изменении показателя степени k возведения числа десять от нуля до бесконечно большого числа можно получить бесконечный ряд целочисленных решений уравнения xn + yn = zn. Так, известно, что числа 3; 4; 5 являются решениями уравнения xn + yn = zn при n = 2. Подстановка в рассматриваемые формулы a = 3 b = 4 при изменении показателя степени k числа десять от нуля до бесконечно большого числа позволяет получить следующий бесконечный ряд целочисленных решений уравнения xn + yn = zn:
k=0 x=3 y=4 z=5
k=1 x=30 y=40 z=50
k=2 x=300 y=400 z=500
k=3 x=3000 y=4000 z=5000
k=4 x=30000 y=40000 z=50000
k=5 x=300000 y=400000 z=500000
……………………………………………
Пример бесконечного ряда решений для случая, когда n = 2 наглядно показывает существование решений уравнения xn + yn = zn в целых бесконечных числах.
Необходимо отметить, что представление конкретных решений уравнения xn + yn = zn фактически только в виде формул не является чем-то необычным. Так и только так точно представляются некоторые дроби или иррациональные числа, которые иначе могут быть записаны лишь в виде фрагментов бесконечных десятичных дробей. Например:
1/3 = 0,333333333333… или √2 = 1,414213562373095048801688724209…
Для записи решений уравнения xn + yn = zn в целых бесконечных числах используется бесконечное числовое произведение, которое рассматривается как произведение бесконечного числа сомножителей u1, u2, u3,…ui,…, то есть выражение вида:
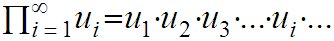
и определяется как предел частичных произведений u1, u2, u3,…ui при i стремящимся к бесконечности [5]. Обычно при использовании бесконечных произведений сомножители u1, u2, u3,…ui,… не равны друг другу и изменяются по величине в зависимости от порядкового номера по тому или иному закону. Кроме этого для практических целей обычно рассматриваются сомножители представленные в виде дробей.
Однако в данном случае все сомножители равны одному числу – 10 и само такое бесконечное числовое произведение стремится к бесконечному целому числу, то есть фактически представляет собой возведение числа 10 в бесконечно большую степень.
В силу невозможности, каким либо образом, использовать бесконечные целые числа в практических целях подобные результаты бесконечных числовых произведений не рассматривались. В связи с этим могут возникать сомнения в справедливости проведения таких вычислений.
Но бесконечные целые числа можно задать и иначе. Их можно задать словесной формулировкой. Например, путем бесконечной записи числа за счет добавления к нему одной и той же цифры или группы цифр или бесконечной записи в число, последовательно вычисляемых цифр какого ни будь иррационального числа.
Например, число, формируемое за счет бесконечного добавления нуля, будет выглядеть следующим образом: 100000000000000000…, а за счет бесконечной записи в число, последовательно вычисляемых цифр иррационального числа √2 будет выглядеть следующим образом: 1414213562373095048801688724209…
При этом не трудно заметить, что получаются идентичные результаты при использовании словесных формулировок для задания бесконечных целых чисел и при использовании бесконечных числовых произведений. И кроме этого задание чисел словесной формулировкой практически исключает все возможности спекуляций по поводу существования целых бесконечных чисел. Ведь именно так формируется, например, бесконечный ряд натуральных чисел и не существует никаких ограничений по общему количеству цифр, которые можно записать в число.
Выдающийся немецкий математик создатель теории бесконечных множеств и теории трансфинитных чисел Георг Фердинанд Людвиг Филипп Кантор (3 марта 1845 – 6 января 1918), по всей видимости, первым отметил, что реальные бесконечные целые числа относятся к так называемой актуальной бесконечности и образуют бесконечный ряд подобных чисел, которые отличны друг от друга и находятся в закономерных числовых отношениях друг к другу и к конечным целым числам. Более того, исследование абсолютно бесконечного ряда реальных целых чисел привело Кантора к усмотрению в этом ряду так называемых числовых классов. Первый числовой класс есть множество конечных целых чисел: 1, 2, 3, … За ним следует второй числовой класс. Он состоит из некоторых бесконечных целых чисел, следующих одно за другим в определенной последовательности. Затем идут 3-й, 4-й числовые классы и так далее [19].
Однако Пьер де Ферма никак не мог быть знаком с работами Кантора, так как умер почти за двести лет до его рождения. И все же, несмотря на это обстоятельство, Ферма вполне мог догадаться о существовании решений уравнения xn + yn = zn среди бесконечных целых чисел. Ведь ему было дано замечать в числах гораздо больше других. Достаточно вспомнить, что именно он открыл следующую после пифагорейцев пару дружественных чисел или именно он заметил, что число 26 является единственным числом, заключенным между квадратом и кубом. Да и сам он в своих работах уделял внимание бесконечным величинам. Именно Пьер де Ферма ввел бесконечно малые величины в аналитическую геометрию. А тут вдруг взял и не заметил решений уравнения xn + yn = zn среди бесконечных целых чисел. Может, у него были причины, в явном виде не показывать наличие таких решений, и поэтому он не стал конкретизировать в своей формулировке теоремы, в каких именно числах отсутствуют решения? Может, он хотел, чтобы остальные математики сами догадались об этом? Подобные розыгрыши были свойственны для Ферма.
В любом случае в результате получилось так, что современная формулировка так называемой Великой теоремы Ферма формально является просто неверной, а формулировка самого Пьера де Ферма, как минимум, выглядит неполной.
Кроме этого необходимо отметить, что бесконечность и бесконечное число являются разными понятиями и имеют различные свойства [5]. Иногда при оперировании с бесконечными числами пытаются применить правила используемые для работы с бесконечностями и естественно приходят к неверным выводам.
С учетом обнаруженных неточностей, формулировку Великой теоремы Ферма следовало бы записать примерно в виде следующего утверждения: нельзя найти конечных рациональных ненулевых чисел x, y и z, которые удовлетворяли бы уравнению xn + yn = zn , если n любое натуральное число большее 2.
В этой формулировке теоремы неважно целочисленными или нет, будут решения, важно чтобы они были в конечных числах. Ведь если решения для конечных рациональных чисел не будут найдены, то в частном случае и решения в конечных целых числах тоже существовать не будут.
В целях преодоления отмеченных проблем в формулировке Великой теоремы Ферма с наименьшими потерями и без необходимости внесения в нее изменений обычно утверждается, что якобы при формулировании теоремы из-за явной очевидности по умолчанию в качестве решений имелись в виду только целые конечные числа.
Конечно, если об этом не было прямо, где-либо написано, то сейчас установить, кто и что в далеком прошлом имел в виду, не представляется возможным. С другой стороны в математике действительно очень часто многое не прописывается, а именно имеется в виду по умолчанию. Происходит это из-за несовершенства используемого в математике языка. Дело в том, что не все функции удается задать только при помощи формул. Часто задавать функции приходится словесными высказываниями или пояснять используемые при задании функций математические формулы словесными высказываниями. При этом в словесных высказываниях уточнения, которые представляются очевидными, часто опускаются. В дальнейшем об этом забывают и в случае применения математических выражений так, как они написаны (без учета уточнений по умолчанию), могут возникать определенные проблемы [6].
Например, если рассмотреть известную из курса физики формулу для вычисления пройденного пути при равномерном прямолинейном движении: s=v·t, то станет очевидным, что эта формула не будет иметь смысла при скорости движения v равной отрицательным значениям или превышающим скорость света и или при отрицательном времени движения t. Таким образом, чисто математически утверждение, что пройденный путь в общем случае выражается через эту формулу, является неправильным. Вообще то при записи, в качестве чисто математического выражения, она должна сопровождаться словесными высказываниями. Такое положение дел в той или иной степени характерно для большинства используемых формул (уравнений).
И Великая теорема Ферма на первый взгляд вроде бы не отличается от большинства используемых формул, действительно сразу была задана преимущественно в виде словесных высказываний, содержащих сравнительно много уточнений, и вроде бы некоторые из них действительно могли бы быть приняты по умолчанию.
Однако эта теорема изначально могла быть сформулирована с использованием математических выражений, которые исключают необходимость применения большинства словесных высказываний и двойного толкования. Но по непонятным причинам этого не было сделано. Например, при формулировании теоремы можно было бы использовать следующее математическое выражение:
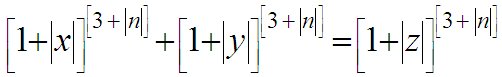
где [ ] – знак, обозначающий целую часть числа или обозначает операцию по отбрасыванию дробной части от результата вычисления выражения, стоящего в прямоугольных скобках.
Тогда формулировка Великой теоремы Ферма сведется всего лишь к утверждению, что данное уравнение не имеет решений в конечных действительных числах.
Действительно, какие бы значения x, y, z и n ни подставлялись в это уравнение, в ходе вычислений будет происходить возврат к уравнению Великой теоремы Ферма в ее классическом виде с учетом словесных высказываний.
Например:
[1+|x|][3+|n|] = [1+|-2|][3+|-2|] = 35
[1+|x|][3+|n|] = [1+|-2,5|][3+|-2,5|] = [3,5][5,5] = 35
[1+|x|][3+|n|] = [1+|0|][3+|0|] = 13
[1+|x|][3+|n|] = [1+|0,7|][3+|0,7|] = [1,7][3,7] = 13
[1+|x|][3+|n|] = [1+|3,7|][3+|4,7|] = [4,7][7,7] = 47
[1+|x|][3+|n|] = [1+|2|][3+|2|] = 35
К аналогичному виду будут приводить преобразования, выполненные и для значений y и z. При этом никакие словесные условия, пояснения, уточнения и тому подобное ни в явном виде, ни по умолчанию не требуются.
Но существовала ли во время жизни Пьера де Ферма возможность задавать уравнения в подобном виде? Действительно обозначение целой части числа или антье от числа ввел К. Гаусс в 1808 году [5]. И это произошло уже после смерти Пьера де Ферма. Однако в 1808 году было введено лишь обозначение, а вот само понятие целой части числа было уже известно очень давно и никаких препятствий для его использования при задании уравнений не существовало. Поэтому сохраняется возможность того, что Пьер де Ферма осознанно предпочел использовать при задании своей теоремы сравнительно расплывчатые словесные формулировки.
Однако, в любом случае, уточнение, что решениями уравнения xn + yn = zn обязательно должны быть конечные числа необходимо, так как в противном случае и в доработанное уравнение можно будет подставлять бесконечные целые числа и соответственно находить решения, удовлетворяющие этому уравнению. И вообще, утверждение, что в Великой теореме Ферма в качестве решений могут использоваться только конечные числа, в этой связи, не выглядит столь уж очевидным.
Кроме этого сделанный анализ формулировки Великой теоремы Ферма наглядно показывает, что эта теорема вовсе не является столь простой и понятной, как о ней принято говорить. А очень известное утверждение о том, что Великая теорема Ферма понятна даже любому школьнику (имеется в виду ее формулировка или смысл), является еще одним мифом, связанным с этой теоремой.
Персидский астроном и математик, уроженец Кума (Иран) Ибн ал-Хусейн (полное имя - Низам ад-Дин ал-Хасан ибн Мухаммад ибн Хусайн ал-Арадж ал-Кумми ан-Найсабури) в своих сочинениях упоминает, что персидский математик и астроном аль-Ходжанди (полное имя - Абу Махмуд Хамид ибн аль-Хизр аль-Ходжанди), уроженец Ходжента (Таджикистан), работавший в Рее (Иран) приблизительно за шестьсот лет до рождения Пьера де Ферма, в десятом веке попытался доказать, что сумма двух кубических чисел не может быть кубическим числом, то есть частный случай Великой теоремы Ферма. К сожалению, само доказательство аль-Ходжанди не сохранилось.
Это считается самой ранней из известных попыток доказательства частного случая Великой теоремы Ферма. В связи с этим не приходится сомневаться, что до Пьера де Ферма были и иные попытки доказательства в том или ином виде его знаменитой теоремы, но информация об этих попытках до нашего времени не сохранилась. Возможно в будущем историки все же обнаружат сведения об этих доказательствах, и возможно среди них даже удастся найти правильное доказательство.
Но пока достоверно известно только, что примерно через шестьсот лет после персидского ученого аль-Ходжанди Пьер де Ферма возродил интерес к проблеме отыскания решений уравнения вида xn + yn = zn для степеней n > 2, записав свое знаменитое замечание: «Невозможно разложить куб на два куба, или биквадрат на два биквадрата, или вообще степень, большую двух, на две степени с тем же самым показателем; я нашел этому поистине чудесное доказательство, однако поля слишком малы, чтобы оно здесь уместилось».
К сожалению, сам Ферма не оставил своего чудесного доказательства. В его записках было обнаружено обоснование лишь частного случая этой теоремы для показателя степени n = 4.
Это обстоятельство позволило позже исследователям утверждать, что у Ферма не было доказательства его теоремы для общего случая. Или если оно и существовало, то было ошибочным.
Однако в случае с Пьером де Ферма отсутствие записанного доказательства ни о чем не говорит, так как для него было обычным делом не оставлять своих доказательств. Ведь умалчивая о сути своих доказательств, он бросал своим современникам вызов, испытывая их способность самостоятельно отыскать доказательство его очередного утверждения, и тем самым поддразнивал своих коллег.
Кроме этого на историю с оставленным Ферма доказательством можно посмотреть и с другой стороны. Ведь можно предположить, что Ферма знал о тупике в своем доказательстве теоремы для показателя степени n = 4 и оставил его просто из желания подшутить над остальными математиками, направив их по заведомо ложному пути.
С другой стороны Ферма не был замечен в распространении ошибочных математических утверждений. Если бы он делал неверные доказательства, то неизбежно бы им часто распространялись бы и ошибочные математические утверждения, но за прошедшие столетия одно за другим были доказаны все утверждения Ферма, содержавшиеся в примечаниях на полях «Арифметики» Диофанта.
Таким образом, нет никаких оснований, подозревать Пьера де Ферма в том, что у него отсутствовало правильное доказательство для общего случая его знаменитой теоремы. И его замечание на полях «Арифметики» Диофанта является всего лишь преднамеренным розыгрышем.
В этой связи следует отметить, что и доказательство частного случая теоремы для показателя степени n = 4 методом бесконечного спуска было изложено им в не полном виде и при решении совершенно другой задачи. Описание этого метода было обнаружено в сорок пятом комментарии к «Арифметике» Диофанта и наиболее полно разработанный Пьером де Ферма метод бесконечного спуска приводится в его письме к Каркави от августа 1659 года: «Поскольку обычные методы, которые изложены в книгах, недостаточны для доказательства столь трудных предложений, я нашел совершенно особый путь для того, чтобы достичь этого. Я назвал этот способ доказательства бесконечным или неопределенным спуском; в начале я пользовался им только для доказательства отрицательных предложений:
- что не существует числа, меньшего на единицу кратного трех, которое составлялось бы из квадрата и утроенного квадрата;
- что не существует прямоугольного треугольника в числах, площадь которого была бы квадратным числом.
Доказательство проводится путем приведения к абсурду таким способом: если бы существовал какой-нибудь прямоугольный треугольник в целых числах, который имел бы площадь, равную квадрату, то существовал бы другой треугольник, меньший этого, который обладал бы тем же свойством.
Если бы существовал второй, меньший первого, который имел бы то же свойство, то существовал бы в силу подобного рассуждения третий, меньший второго, который имел бы то же свойство, и, наконец, четвертый, пятый, спускаясь до бесконечности.
Но если задано число, то не существует бесконечности, по спуску меньших его (я все время подразумеваю целые числа). Откуда заключают, что не существует никакого прямоугольного треугольника с квадратной площадью».
Применяя метод бесконечного спуска для доказательства отсутствия решений в целых числах для уравнения x4 + y4 = z4 Ферма начал с предположения о существовании гипотетического решения в целых числах (x1, y1, z1).
При изучении свойств чисел (x1, y1, z1) Ферма показал, что если бы такое гипотетическое решение действительно существовало, то существовало бы меньшее решение (x2, y2, z2). Рассматривая это новое решение, Ферма смог показать, что если бы оно существовало, то существовало бы еще меньшее решение (x3, y3, z3) и так далее.
Ферма обнаружил нисходящую лестницу решений, которая теоретически могла бы продолжаться неограниченно, порождая все меньшие и меньшие решения. Но x, y и z должны быть целыми или натуральными числами, поэтому нескончаемая нисходящая лестница невозможна, потому что должно быть наименьшее целочисленное решение.
Полученное противоречие доказывает, что начальное предположение о существовании решения (x1, y1, z1) было ложным. Итак, используя метод бесконечного спуска, Ферма доказал, что при n = 4 уравнение xn + yn = zn не может иметь целочисленных решений.
Метод бесконечного или неопределенного спуска стал одним из наиболее мощных средств исследования диофантовых уравнений (Приложение 3).
После П. Ферма его с успехом применяли Л. Эйлер и Л. Лагранж, а в наши дни – Л. Дж. Морделл, А. Вейль и другие. При этом метод был распространен на проблемы решения уравнений в рациональных числах. Но применить данный метод для общего случая Великой теоремы Ферма мешает неединственность разложения целых чисел алгебраических колец в произведение простых сомножителей из того же кольца.
Кроме этого необходимо отметить, что метод бесконечного спуска позволяет доказать существование решений уравнения xn + yn = zn в целых бесконечных числах, так как для любого решения в целых бесконечных числах можно находить до бесконечности меньшие решения в целых бесконечных числах и так никогда и не дойти до наименьшего решения. Поскольку наименьшего решения в целых бесконечных числах просто не существует. Например, для уравнения x4 + y4 = z4 можно записать его решение в целых бесконечных числах:

Меньшее решение в целых бесконечных числах можно получить следующим образом:
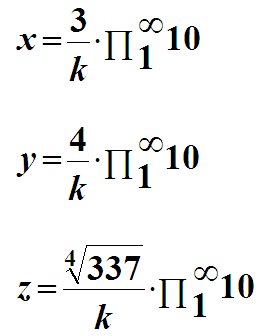
где k – число большее единицы, то есть может последовательно выбираться из ряда натуральных чисел: 2, 3, 4, 5, … и чем больше по величине будет k, тем меньшими будут решения уравнения x4 + y4 = z4 в целых бесконечных числах (x, y, z). Но поскольку ряд натуральных чисел бесконечный, то и число k можно увеличивать бесконечно, а это означает, что найти наименьшее решение (x, y, z) невозможно.
Таким образом, метод бесконечного спуска может быть применен для доказательства Великой теоремы Ферма только для случая, когда решения уравнения xn + yn = zn выражаются в конечных числах. И это обстоятельство дополнительно свидетельствует в пользу того, что Пьер де Ферма мог знать о существовании решений уравнения xn + yn = zn в целых бесконечных числах.
В последствии ряд математиков пытались приспособить метод бесконечного спуска Ферма для решения уравнения xn + yn = zn в целых числах при n, отличных от четырех, но всякий раз попытка распространить метод приводила к каким-нибудь проблемам в логике. Пока живший в XVIII веке Леонард Эйлер не попытался использовать для доказательства Великой теоремы Ферма теорию комплексных чисел, не имеющую, казалось бы, никакого отношения к поставленной задаче и не заставил метод бесконечного спуска работать для случая n = 3. О чем Леонард Эйлер сообщил в своем письме к прусскому математику Христиану Гольдбаху в августе 1753 года.
Так через сто лет после смерти Пьера де Ферма впервые удалось совершить значительный прорыв на пути к решению его проблемы.
Эйлер надеялся, что доказав Великую теорему Ферма для случая n = 3 он сможет экстраполировать полученный результат на уравнения xn + yn = zn со всеми остальными показателями степени n. Но повторить успех при других значениях n ни самому Эйлеру ни другим математикам восемнадцатого века не удалось. К сожалению, все попытки применить те же рассуждения к другим значениям вплоть до бесконечности закончились провалом. Более того, даже само доказательство Эйлера содержало пробел [7], который, впрочем, был впоследствии преодолен.
В связи с этим уже доказательство Леонарда Эйлера не являлось элементарным и вряд ли могло иметь отношение к доказательству Пьера де Ферма и не могло приближать к решению задачи по восстановлению утраченного доказательства Ферма.
Однако выяснилось, что доказательство Великой теоремы Ферма для случая n = 4 остается в силе при показателе степени n равном 8, 12, 16, 20…. и так далее для любой степени, кратной четырем. Действительно, любое число, представимое в виде восьмой, а также двенадцатой, шестнадцатой, двадцатой и так далее степени некоторого числа, представимо и в виде четвертой степени какого-то другого целого числа. Например, число 256 равно 28, но оно равно и 44 или число 4096 равно 212, но оно же равно и 84. Следовательно, любое доказательство, которое справедливо для четвертой степени, остается в силе для восьмой и любой другой степени, кратной четырем. На основе того же принципа можно утверждать, что доказательство Леонарда Эйлера для случая n = 3 автоматически распространяется и на случаи, когда n = 6, 9, 12, 15…. и так далее для любой степени, кратной трем. Например, число 64 равно 26, но оно равно и 43 или число 512 равно 29, но оно же равно и 83. Тем самым Великая теорема Ферма оказалась верной сразу для многих чисел n. Вот такие рассуждения существовали раньше и продолжают существовать в наше время.
Тут необходимо обратить внимание на то, что такое распространение частных случаев доказательства Великой теоремы Ферма на все кратные степени являлось ошибочным. Например, если рассмотреть показатель степени n равный 4, 6, 8, 10…. и так далее для любой степени, кратной двум, то любое число, представимое в виде четвертой, а также шестой, восьмой, десятой и так далее степени некоторого числа, тоже будет представимо и в виде второй степени какого-то другого целого числа. Действительно, число 16 равно 24, но оно равно и 42 или число 4096 равно 212, но оно же равно и 642. Теперь, следуя выше приведенным рассуждениям, приходим к выводу, что Великая теорема Ферма не верна для всех четных значений показателя степени n, так как уравнение x2 + y2 = z2 имеет решения в конечных целых числах. Однако известно, что уравнение xn + yn = zn при n равном 4, 6, 8, 10… и так далее не имеет решений в конечных целых числах, то есть пришли к противоречию. В связи с тем, что подобная ошибка в рассуждениях сравнительно распространена в дальнейшем при описании предлагавшихся вариантов доказательства Великой теоремы Ферма на нее не всегда будет указываться.
При этом в качестве особенно ценного рассматривалось доказательство Леонарда Эйлера Великой теоремы Ферма для случая n = 3, так как предполагалось, что для доказательства теоремы в общем виде достаточно обосновать утверждение Ферма лишь для простых чисел n. Действительно, пусть, например, уравнение xn + yn = zn имеет решение при n = q·r, где q и r – некоторые простые числа, то есть числа не кратные ни одному целому числу, кроме единицы и самого себя. Тогда уравнение xn + yn = zn можно будет записать в следующем виде: xq·r + yq·r = zq·r. Введя обозначения a = xq, b = yq, c = zq, приходим к уравнению ar + br = cr. Тем самым, из существования решения уравнения xn + yn = zn для составного числа n следует существование решения этого же уравнения для меньшего показателя степени – простого делителя r числа n. Таким образом, установив желаемый результат лишь для простых значений показателя степени n, будет получен аналогичный результат для произвольного значения показателя степени n, и тем самым будет окончательно доказана Великая теорема Ферма в общем виде. Но, к сожалению, перечень простых чисел бесконечен. Следовательно, несмотря на то, что можно исключить из рассмотрения все уравнения при составных значениях показателя степени n, количество уравнений xn + yn = zn с простыми значениями показателя степени n по-прежнему останется бесконечным.
Хотя сожалеть было, в общем-то, и не о чем и исключать из рассмотрения, во всяком случае, по рассмотренным основаниям никакие значения показателя степени n было нельзя. Действительно, уже при разложении на простые множители первого составного числа n = 4 получим, что q = 2 и r = 2. Так как уравнение x2 + y2 = z2 имеет бесконечно много решений в конечных целых числах, а уравнение x4 + y4 = z4 неразрешимо в конечных целых числах, то приходим к очередному противоречию.
Конечно, можно попытаться исключить простое число 2 из рассмотрения. И, разумеется, это уже было предложено сделать. Но в этом случае к бесконечному количеству простых значений показателя степени n прибавится еще и бесконечное количество составных чисел, образованных с участием числа 2.
После прорыва, осуществленного Эйлером, не было ни малейшего продвижения, и к началу XIX века за Великой теоремой Ферма установилась устойчивая репутация самой трудной проблемы в теории чисел.
Поиски доказательства Великой теоремы Ферма возобновились с новой силой только после предложения француженкой Софи Жермен качественно нового способа исследования уравнения xn + yn = zn.
Живя в эпоху шовинизма и предрассудков, Софи Жермен вынуждена была представляться неким месье Лебланом. Поэтому именно от месье Леблана Гаусс получил письма, в которых Софи Жермен изложила ему свои предложения. В частности, вместо того чтобы доказывать неразрешимость уравнения xn + yn = zn, она предложила установить, каким свойствам должно удовлетворять его решение в случае, если таковое существует. Согласно ее утверждению, если n есть простое число, а число 2·n + 1 также является простым, то из равенства xn + yn = zn вытекает, что хотя бы одно из трех чисел x, y, z делится на n. В частности, если уравнение x5 + y5 = z5 имеет решение, то хотя бы одно из чисел x, y, z должно непременно делиться на пять. Из теоремы Софи Жермен следовало, что Великая теорема Ферма распадается на два специфических случая: когда ни одно из чисел x, y, z не делится на n и когда одно из них делится на n. Таким образом, Жермен показала специалистам по теории чисел, как исключить целую группу случаев с простыми значениями n, и объединенными усилиями ее коллеги продолжали доказывать теорему для одного простого значения n за другим.
В 1825 году метод Софи Жермен был успешно применен Густавом Леженом Дирихле и Адриеном Мари Лежандром. И Лежандру, и Дирихле независимо друг от друга удалось доказать Великую теорему Ферма при n = 5, причем оба основывали свои доказательства на рассуждениях Софи Жермен и именно ей были обязаны своим успехом.
Еще один прорыв осуществил четырнадцатью годами спустя француз Габриель Ламе. Он внес некоторые усовершенствования в метод Жермен и доказал Великую теорему Ферма при простом значении n = 7 (1839 г). В дальнейшем были получены доказательства Великой теоремы Ферма еще и для случаев n = 11 и 13, но общего доказательства на этом пути получить не удалось.
После прогресса, достигнутого благодаря работам Софи Жермен, Французская Академия Наук установила премию: золотую медаль и 3000 франков, тому математику, который сумеет доказать Великую теорему Ферма в общем виде.
Конкурс был назначен на 1853 год и затем продлен до 1856 года. Секретарю конкурса были представлены одиннадцать работ. Ни в одной из них поставленный вопрос решен не был.
Несмотря на значительное материальное вознаграждение в борьбе за первую премию в истории Великой теоремы Ферма приняли участие только профессиональные математики. А вот дилетанты-любители тогда практически не откликнулись. Видимо в девятнадцатом веке система образования и распространения научной информации были еще недостаточно развиты.
Первого марта 1847 года на заседании Французской Академии Наук определились два главных претендента на получение премии Габриель Ламе и Огюстен Луи Коши, которые пытались использовать схожие подходы к доказательству теоремы.
Хотя ни Ламе, ни Коши не располагали полным доказательством теоремы, оба соперника страстно желали подкрепить свои притязания, и двадцать второго марта представили Французской Академии Наук имевшиеся у них на тот момент результаты в запечатанных конвертах. В то время это делалось для того, чтобы в последствии в случае возникновения споров о первенстве математик мог подтвердить свой приоритет.
Однако после публикации этих материалов возникли сомнения в корректности возможного доказательства. И после обнародования двадцать четвертого мая Жозефом Лиувиллем письма Эрнста Куммера из Германии все надежды Ламе и Коши на доказательство Великой теоремы Ферма были окончательно развеяны.
Куммер заметил, что оба француза допускают одну и туже ошибку. По его мнению, основная проблема заключалась в том, что доказательства Коши и Ламе опирались на использование свойства целых чисел, известного под названием единственности разложения на простые множители. Это свойство означает, что существует только одна возможная комбинация простых чисел, произведение которых дает данное целое число. Например, 15 = 3·5; 16 = 2·2·2·2; 18 = 2·3·3. Единственность разложения на простые множители для всех натуральных чисел в настоящее время называется основной теоремой арифметики. Эта теорема, многократно и без каких либо проблем успешно применялась при решении различных задач в натуральных числах. Но оба, представленных Французской Академии Наук доказательства использовали мнимые числа. И Куммер обратил внимание на то, что, хотя теорема о единственности разложения на множители выполняется для всех натуральных чисел, она не обязательно должна выполняться для мнимых чисел.
Так как умножение комплексных чисел, то есть чисел представляющих собой комбинацию действительных и мнимых чисел, производится по более сложным правилам, чем умножение действительных чисел, то появляются дополнительные способы разложения таких чисел на множители. И в связи с этим при использовании в доказательстве мнимых чисел речь идет уже не о единственности разложения, а о выборе одного из вариантов разложения на множители.
Таким образом, утрата единственности разложения на множители нанесла тяжелый урон доказательствам Коши и Ламе, но не уничтожила их полностью. Предполагалось, что доказательства должны продемонстрировать отсутствие решений в целых числах у уравнения xn + yn = zn, где n — любое целое число, большее 2. Куммер показал, что, используя дополнительные ухищрения, можно восстановить единственность разложения на множители при некоторых значениях n. Например, проблему единственности разложения можно обойти для всех простых чисел, не превышающих n = 31. Но при n = 37 избавиться от трудностей не так просто. Среди других, прочих чисел, меньших 100, особенно трудно доказать Великую теорему Ферма при n = 59 и n = 67. Это так называемые нерегулярные простые числа, разбросанные среди остальных чисел, стали камнем преткновения на пути к полному доказательству.
Куммер отметил, что не существует известных математических методов, которые позволили бы сразу рассмотреть все нерегулярные простые числа. Но он полагал, что, тщательно подгоняя существующие методы к каждому нерегулярному простому числу в отдельности, с ними удастся справиться. Разработка таких, индивидуальных для каждого числа, методов было бы делом медленным и чрезвычайно трудным, и, что еще хуже, множество нерегулярных простых чисел было бесконечным. Поэтому рассмотрение нерегулярных простых чисел по одному силами даже всего мирового математического сообщества было бы бесконечным.
Однако идеи Куммера все же позволили существенным образом продвинутся на пути доказательства Великой теоремы Ферма. В частности, была доказана неразрешимость уравнения xn + yn = zn, где n для всех значений n меньше ста. Но полного доказательства Великой теоремы Ферма Куммер так и не добился.
После работ Эрнста Куммера надежды найти доказательство ослабли, как никогда прежде. Кроме того, в математике начали развиваться новые направления и математики сосредотачивали свои усилия в первую очередь именно на них, а Великая теорема Ферма все больше начинала восприниматься как романтическая мечта прошлого. Большинство профессиональных математиков стали считать поиск доказательства Великой теоремы Ферма безнадежным делом и решительно отказывались тратить свое время на такое бесполезное занятие.
Однако совершенно неожиданно в начале двадцатого века проблема Пьера де Ферма вновь привлекла к себе всеобщее внимание благодаря некоему Паулю Вольфскелю, немецкому промышленнику из Дармштадта.
Пауль Вольфскель происходил из очень богатой семьи и состоялся, прежде всего, как успешный предприниматель. Но в университете он изучал математику и после его окончания продолжил на любительском уровне заниматься теорией чисел. В частности, Вольфскель не отказался от мысли найти доказательство Великой теоремы Ферма. И эта проблема очень сильно его увлекала. Правда, внести заметный вклад в поиски доказательства Великой теоремы Ферма он так и не смог.
Еще с его именем и проблемой Пьера де Ферма связана одна легенда. Утверждается, что Вольфскель из-за неразделенной любви решил покончить с собой, но пропустил им же самим назначенное время самоубийства, увлекшись доказательством Великой теоремы Ферма, а потом и вовсе передумал сводить счеты с жизнью.
В результате под влиянием всех этих обстоятельств после своей смерти в 1908 году в своем завещании он оставил значительную часть своего состояния в качестве премии тому, кто сумеет доказать Великую теорему Ферма. Премия в 100000 марок, весьма значительная сумма по тем временам, была той суммой, которую Вольфскель счел своим долгом уплатить в награду за головоломную проблему, спасшую ему жизнь.
Деньги были положены на счет Королевского научного общества Гёттингена, которое в 1908 году официально объявило о проведении конкурса на соискание премии Вольфскеля. Текст объявления приведен в Приложении 4. В этой организации когда-то работали такие знаменитые ученые как Гаусс, Дирихле, Риман, а в то время Гильберт, Клейн и Минковский.
Комиссия выплатила бы 100000 марок первому математику, который доказал бы, что Великая теорема Ферма верна, но тот, кто доказал бы, что теорема Ферма не верна, не получил бы ничего. Возможно, это сыграло свою отрицательную роль при дальнейших попытках восстановить утраченное доказательство Ферма. Ведь, по всей видимости, именно из-за желания получить премию никто из тех, кто еще продолжал заниматься этой проблемой, не хотел замечать выше описанные и достаточно очевидные проблемы в формулировке теоремы, а это в свою очередь не позволило скорректировать направления исследований.
О премии Вольфскеля было объявлено во всех математических журналах, и весть о конкурсе быстро распространилась по всей Европе. Несмотря на широкую рекламную кампанию и дополнительный побудительный стимул в виде огромной премии, Комиссии Вольфскеля не удалось вызвать особый интерес у профессиональных математиков.
Работавший в то время в Гёттингенском университете Давид Гильберт, которого называли последним из великих математиков, даже говорил, что ему доказывать Великую теорему Ферма невыгодно. Действительно, на проценты с премии Вольфскеля Гёттингенский университет приглашал к себе математиков со всего мира. При этом еще в 1900 году на Международном конгрессе математиков в Париже Гильберт выступил с грандиозной программой развития математики двадцатого века. Среди поставленных им двадцати трех проблем десятая проблема предполагала разработку метода позволяющего ответить на вопрос, будет ли диофантово уравнение общего вида иметь решение. Понятно, что положительное решение десятой проблемы Гильберта будет означать автоматическое доказательство или опровержение Великой теоремы Ферма, связанной, как известно, с одним конкретным диофантовым уравнением. Поэтому трудно сказать, пытался ли Гильберт доказать Великую теорему Ферма?
К сожалению, в 1970 году советский математик Юрий Матиясевич дал отрицательное решение десятой проблемы Гильберта [8]. Он показал, что принципиально невозможно разработать универсальный алгоритм, который позволил бы установить, будет ли произвольное диофантово уравнение иметь решение или нет. Теория диофантовых уравнений оказалась более сложной, чем об этом думали математики в начале двадцатого века.
Объявление о премии за доказательство Великой теоремы Ферма не вдохновило профессиональных математиков, но побудило заняться решением загадки Ферма огромное количество любителей. И таких людей было столь много, что для них были введены даже специальные термины «ферматисты» или «ферматики» - люди, пытающиеся доказать теорему Ферма элементарными методами и зачастую не имеющие специального математического образования.
Уже несколькими неделями спустя после объявления конкурса на соискание премии Вольфскеля на Гёттингенский университет обрушилась лавина составленных дилетантами доказательств. В результате их рассмотрения все они были признаны ошибочными. О рассмотрении же присланных доказательств необходимо сказать особо.
Так утверждается, что независимо от того, кто был отправителем того или иного доказательства, каждое из них скрупулезно изучалось на тот случай, если неизвестному любителю все же удастся найти столь давно разыскиваемое доказательство. Возможно, с самого начала, какое-то непродолжительное время так оно и было.
Деканом математического факультета Гёттингенского университета с 1909 по 1934 годы был профессор Эдмунд Ландау. Именно на него легла обязанность разбирать все доказательства, присланные на соискание премии Вольфскеля.
Ландау был вынужден то и дело прерывать свои собственные исследования, поскольку ему нужно было разбирать десятки поступавших к нему ежемесячно доказательств. Чтобы справиться с ситуацией, профессор Ландау попросил напечатать несколько сотен карточек, на которых значилось:
«Уважаемый(ая) . . . . . . . .
Благодарю Вас за присланную Вами рукопись с доказательством Великой теоремы Ферма. Первая ошибка находится на стр … в строке … Из-за нее все доказательство утрачивает силу.
Профессор Э.М. Ландау»
Каждое из полученных доказательств вместе с отпечатанной карточкой Ландау вручал одному из своих студентов и просил его заполнить пробелы.
Такое рассмотрение доказательств очень трудно назвать скрупулезным. При таком рассмотрении вполне можно было пропустить правильное доказательство. В результате отсутствуют основания для признания абсолютно всех первых доказательств ошибочными. Однако именно это всегда и утверждалось.
Несмотря на пренебрежительное отношение, доказательства продолжали поступать непрерывным потоком в течение нескольких лет даже после того, как премия Вольфскеля в значительной мере обесценилась из-за гиперинфляции после первой мировой войны. Но и качество рассмотрения доказательств не улучшилось.
Составить представление о работе Комиссии по премии Вольфскеля позволяет письмо доктора Ф. Шлихтинга Паулю Рибенбойму [9]:
«Уважаемый сэр!
Общее число представленных к настоящему времени «решений» неизвестно. В первый год (1907-1908 гг.) в анналах Академии было зарегистрировано 621 решение. В настоящее время в Академии хранится стопка бумаг, толщиной около трех метров, с материалами переписки по проблеме Ферма. В последние десятилетия работа с письмами производилась следующим образом. Секретарь Академии делил поступающие рукописи по следующим категориям: 1) полная чепуха, которая немедленно отсылалась обратно; 2) материал, который по крайней мере внешне походил на математику.
Вторая часть корреспонденции передавалась математическому факультету, где работа по прочтению рукописей, нахождению ошибок и ответу авторам поручалась одному из ассистентов. Сейчас очередная жертва - это я. Каждый месяц поступают 3-4 письма, на которые я должен отвечать. В этих письмах масса интересного и любопытного материала. Например, один из корреспондентов прислал половину доказательства и пообещал прислать вторую, если мы выплатим 1000 марок авансом. Другой корреспондент пообещал мне 1% от своих доходов от своих публикаций, интервью на радио и телевидении, когда он станет знаменитым, если только я окажу ему сейчас поддержку. В противном случае он угрожал послать свое доказательство в адрес математического факультета какого-нибудь российского университета и тем самым лишить нас славы его открывателей. Время от времени кто-нибудь из авторов «доказательств» наведывается в Гёттинген и настаивает на личной встрече и обсуждении.
Почти все «доказательства» написаны на самом элементарном уровне (и используют обозначения, заимствованные из высшей математики и, быть может, некоторых плохо усвоенных работ по теории чисел). Тем не менее, понять их очень трудно. В социальном плане отправители нередко оказываются людьми с техническим образованием, но с не сложившейся карьерой, которые пытаются теперь достичь успеха с помощью доказательства Великой теоремы Ферма. Некоторые рукописи я передал психиатрам, и те диагностировали тяжелую шизофрению.
Одно из условий в завещании Вольфскеля состояло в том, что Академия была должна ежегодно печатать извещение о конкурсе на соискание премии в главных математических журналах. Но уже через несколько первых лет журналы отказались печатать уведомление о конкурсе потому, что редакции оказались заваленными письмами и сумасшедшими рукописями. Надеюсь, что эта информация представит для Вас некоторый интерес.
Искренне Ваш Ф. Шлихтинг»
Автор письма больше сосредоточен на личных качествах претендентов на получение премии, чем на содержании доказательств. К содержанию доказательств он демонстрирует заранее негативное отношение.
Однако далеко не все доказательства Великой теоремы Ферма попадали в Комиссию по премии Вольфскеля Гёттингенского университета, большая часть была направлена их авторами в различные высшие учебные заведения, научные организации, в редакции журналов и издательства, а так же лично известным ученым буквально по всему миру.
Отдельные доказательства даже были опубликованы в основном в ненаучной прессе. Так среди них наиболее известны брошюра В. И. Будкина, изданная в 1975 году в Ярославле под названием «Методика познания „истины“. Доказательство Великой теоремы Ферма» и книга Л. Ш. Райхеля «Великая теорема», изданная в Ленинграде в 1990 году.
С появлением сети Интернет количество подобных самостоятельных публикаций вариантов доказательства Великой теоремы Ферма, правда, в электронном виде, многократно увеличилось и продолжает расти.
Министерство образования и науки Украины в 2001 году даже выдало Л. В. Шаповаловой и Г. А. Середкину свидетельство о регистрации авторских прав на произведение «Доказательство теоремы Ферма», но не рассматривая представленное доказательство по существу.
В большинстве случаев подобные доказательства оставлялись без внимания и ответа. А о получении рецензии и речи не могло идти. Более того, игнорирование - это еще был не самый плохой вариант, встречались и откровенные насмешки. Так один любитель пошутить над не вполне здоровыми людьми отвечал авторам присланных доказательств: «У меня есть замечательное опровержение присланного Вами доказательства, но, к сожалению, эта страница недостаточно велика, чтобы вместить его».
Нетрудно представить, какой благосклонный прием ожидал бы в Комиссии по премии Вольфскеля чудесное доказательство самого Пьера де Ферма. Ведь написано оно на самом элементарном уровне, да еще и устаревшим математическим языком семнадцатого века, а потому мало понятно. Конечно Пьер де Ферма, как автор столь странно написанного доказательства в лучшем случае был бы принят за ферматиста, а в худшем за шизофреника, а его произведение по существу рассмотрели разве что психиатры.
Из всей этой истории с любительскими доказательствами Великой теоремы Ферма существует одно нехорошее следствие – отсутствие уверенности у любого автора правильного доказательства теоремы, что оно действительно стало первым после доказательства самого Пьера де Ферма. Так как сейчас уже отсутствует возможность доказать, что абсолютно все любительские доказательства были неправильными.
В первой половине двадцатого века профессиональные математики сколь ни будь заметно, не отметились в решении проблемы Ферма. В этот период времени косвенно с доказательством Великой теоремы Ферма связывают лишь некоторые работы Курта Гёделя.
В 1931 году Курт Гёдель опубликовал свою работу «Uber formal unentscheidbare Satze der Principia Mathematica und verwandter Systeme», в которой содержались его так называемые теоремы о неразрешимости. Из высказанных им идей следовало, что некоторые проблемы математики могут оказаться неразрешимыми. И было сделано предположение (правда не самим Гёделем), что Великая теорема Ферма относится к таким неразрешимым проблемам математики. Таким образом, работа Гёделя о неразрешимости внесла элемент сомнения в вопрос о том, разрешима ли проблема Ферма.
Конечно эти рассуждения, как и многие другие, были ошибочными и работы Гёделя никак небыли связаны с проблемой Ферма. Ведь если проблема Ферма неразрешима в общем виде, то не должна ли она быть неразрешима и для частных случаев? Но Великая теорема Ферма к тридцатым годам двадцатого века была уже доказана для многих частных случаев.
К восьмидесятым годам двадцатого века с использованием компьютеров неразрешимость уравнения xn + yn = zn в натуральных числах была установлена для всех n меньших или равных 2125000 (З. Вагштафф, 1976 г.). Если принять во внимание, что число 2125000 записывается 37628-ю цифрами, то поиски контр примера к Великой теореме Ферма стали считать совершенно безнадежным занятием.
Вот только предположения о том, что можно установить при помощи компьютера неразрешимость уравнения xn + yn = zn в натуральных числах хотя бы для совсем небольших значений n были ошибочными. Дело в том, что решения (x, y, z) могут выражаться в сколь угодно больших числах и более того даже в бесконечных числах, с которыми ни один компьютер, ни сейчас, ни в будущем работать не может.
Получается, что если утверждение о неразрешимости уравнения xn + yn = zn в натуральных числах для всех n меньших или равных 2125000 истинно, то данное уравнение неразрешимо и в целых бесконечных числах. Однако выше было показано, что это уравнение имеет бесконечно много решений в целых бесконечных числах. Таким образом, пришли к противоречию.
Причем введение ограничения, заключающегося в том, что решения (x, y, z) могут выражаться только в конечных числах, принципиально ситуацию для компьютерных доказательств не улучшит. Поскольку любой компьютер может корректно работать только с числами определенной величины (длины). При превышении этой величины компьютер начинает искажать результаты вычислений и таким результатам доверять нельзя.
Например, вычислим значение z в уравнении x4 + y4 = z4 при помощи обычного «бытового» компьютера для достаточно больших
x = 40000000000000000000000000000000 и
y = 20000000000000000000000000000000
400000000000000000000000000000004 +
+200000000000000000000000000000004 = 2,72·10126
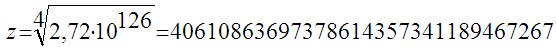
Именно такое натуральное число 40610863697378614357341189467267 выдаст встроенный калькулятор компьютера. Но не стоит спешить радоваться, что при помощи компьютера удалось найти контр пример в конечных целых числах для Великой теоремы Ферма. Действительно число 40610863697378614357341189467267 очень близко к решению уравнения x4 + y4 = z4, но все же на очень маленькую величину отличается от точного решения. Вот эту очень маленькую величину компьютер по чисто техническим причинам и не смог отобразить и просто ее отбросил.
Причем эта проблема, связанная с осуществлением вычислений на компьютере принципиально не устранима, так как если сделать компьютер способный оперировать числами, состоящими из миллиона цифр, то всегда можно будет задать число, состоящее из миллиона цифр плюс одна цифра, что приведет к появлению проблемы, а если сделать компьютер способный оперировать числами, состоящими из миллиарда цифр, то всегда можно будет задать число, состоящее из миллиарда цифр плюс одна цифра, что опять приведет к появлению проблемы и так можно продолжать до бесконечности.
Таким образом, использование компьютера может помочь только в одном случае, если в ходе вычислений удастся обнаружить контр пример среди чисел, с которыми компьютер может работать корректно. Отсутствие же контр примера в такой ситуации ничего не подтверждает и не опровергает.
К середине двадцатого века сформировались уже устойчивые представления о том, что все возможные методы доказательства Великой теоремы Ферма были неоднократно использованы и не привели к желаемому результату. Поэтому те математики, которые еще продолжали попытки найти доказательство теоремы, все больше сосредотачивались на самых последних достижениях математики двадцатого века. То есть перешли к попыткам доказать Великую теорему Ферма любой ценой, что означало автоматический отказ от собственно решения проблемы Ферма или можно сказать попытки ответить на вызов брошенный всем математикам Пьером де Ферма еще в семнадцатом веке.
Одним из таких совершенно новых достижений, или если сказать точнее, направлений математики стала сформулированная в 1955 году молодым японским математиком Ютакой Таниямой следующая гипотеза: всякая эллиптическая кривая с рациональными коэффициентами модулярна. Данная гипотеза относилась к алгебраической геометрии, разделу математики, в котором изучаются геометрические объекты, связанные с алгебраическими уравнениями.
Эллиптической кривой называется кривая на плоскости, заданная уравнением y2 = x3 + a·x2 + b·x + c, где a, b, c – рациональные числа. Уравнения такого вида так же еще называются кубическими. Истоком теории эллиптических кривых является понятие эллиптического интеграла, которое появилось еще в конце семнадцатого века в связи с вычислением длины дуги эллипса.
Проблема эллиптических кривых, как и проблема доказательства Великой теоремы Ферма, заключается в вопросе, имеют ли соответствующие им уравнения целочисленные решения, и если имеют, то сколько.
Модулярная форма представляет собой специфическую функцию очень богатую свойствами симметрии, что позволяет ей преобразовываться самой в себя. То есть модулярные формы можно подвергать трансляциям (параллельным переносам, или сдвигам), перестраивать, переставлять фрагменты, отражать в зеркалах и поворачивать бесконечно многими способами, и при этом они останутся неизменными, что делает их наиболее симметричными математическими объектами.
Ни нарисовать, ни даже вообразить модулярную форму невозможно. Модулярную форму можно представлять как функцию, область определения которой находится в двух измерениях, но и область значений которой также двумерна. Поэтому график такой функции может существовать только в четырехмерном пространстве.
Разумеется, существуют условия модулярности эллиптической кривой, и эти условия слишком сложны, для того чтобы, без дополнительных обоснований, можно было поверить в существование хотя бы одной модулярной эллиптической кривой. Поэтому понятно почему, вначале гипотезу Ютаки Таниямы о том, что абсолютно все эллиптические кривые с рациональными коэффициентами модулярны не принял всерьез ни один профессиональный математик. Тем более что Танияма не смог обосновать наличие связи между теориями эллиптических кривых и модулярных форм, а смог привести лишь серию примеров связанных друг с другом эллиптических кривых и модулярных форм.
Однако постепенно к 1970-м годам усилиями японского математика Г. Шимуры и французского математика А. Вейля удалось получить достаточно серьезные подтверждения гипотезы Таниямы, но строго доказать эту гипотезу они все же не смогли.
Наконец в 1984 году немецкий математик Герхард Фрей указал на возможную связь гипотезы Таниямы с Великой теоремой Ферма. Его рассуждения сводились к следующему.
Пусть Великая теорема Ферма не верна, то есть для какого-то числа n > 2 верно равенство xn + yn = zn в целых конечных числах, то есть A + B = C, где A = xn , B = yn , C = zn.
После этого Фрей преобразовал уравнение Ферма xn + yn = zn с учетом гипотетических его решений к следующему виду:
y2 = x·(x – A)·(x – C) = x3 – (A + C)·x2 + A·C·x.
То есть преобразовал уравнение Ферма xn + yn = zn в кубическое уравнение и тем самым показал, что кривая, соответствующая этому уравнению, является эллиптической. И действительно уравнение, полученное Фреем, легко может быть представлено в виде классического уравнения эллиптической кривой: y2 = x3 + a·x2 + b·x + c, где a = A + C, b = A· C, c = 0. Сразу необходимо отметить, что существовать эта эллиптическая кривая будет только в том случае, если будут существовать конкретные значения коэффициентов a, b, c. В противном случае эллиптическая кривая просто будет не задана. Так как сам Фрей это обстоятельство никак не пояснял.
Затем он заявил, что эта кривая обладает такими свойствами, что ей никак не может соответствовать какая-либо модулярная форма. Это, в свою очередь, вступает в противоречие с гипотезой Таниямы, согласно которой любая эллиптическая кривая должна соответствовать некоторой модулярной форме. А в результате получается альтернатива: либо эта гипотеза верна, и тогда первоначальное предположение о существовании решения уравнения Ферма не соответствует действительности (а значит, справедлива Великая теорема Ферма), либо рассматриваемая гипотеза не верна. Таким образом, в случае обоснования гипотезы Таниямы автоматически будет получено доказательство Великой теоремы Ферма.
Однако не следует думать, что рассуждения Герхарда Фрея возникли на пустом месте. Еще в начале девятнадцатого века один из основоположников теории эллиптических интегралов Карл Якоби предположил, что эта теория может найти применение для исследования диофантовых уравнений. А в конце девятнадцатого века уже Герман Минковский закладывает основы нового раздела теории чисел – геометрии чисел. Минковский показал, что некоторые геометрические конструкции могут быть с успехом использованы для обоснования многих утверждений теории чисел.
Но, несмотря на все имеющиеся основания, необходимо обратить внимание на существование ряда вопросов к рассуждениям Фрея. Так как на эти вопросы до сих пор никто никаких ответов не дал.
Эллиптическая кривая существует только в том случае, если коэффициенты a, b, c будут выражаться в конкретных числах, а если они не были представлены в виде конкретных чисел, то вне зависимости от причин этого, эллиптической кривой просто нет или можно сказать, что конкретная эллиптическая кривая не была задана. Незаданной эллиптической кривой никак не может соответствовать какая-либо модулярная форма. Если не были заданы ни эллиптическая кривая, ни модулярная форма, то рассматривать в рамках гипотезы Таниямы собственно говоря становится и нечего. Иначе говоря, для того чтобы появились основания для использования гипотезы Таниямы при доказательстве Великой теоремы Ферма необходимо доказать, что объект «кривая Фрея» действительно является конкретной эллиптической кривой. То есть показать, что конкретные значения коэффициентов a, b, c не гипотетически, а реально существуют, а это сделать невозможно. Ведь контр пример для Великой теоремы Ферма до сих пор никто не нашел.
Поскольку даже далеко не все профессиональные математики хорошо разбираются в теории эллиптических кривых и модулярных форм, а также уверенно владеют терминологией этих теорий, то для обычного читателя поясним все здесь сказанное на простом примере.
Пусть Великая теорема Ферма не верна, то есть для какого-то числа n > 2 верно равенство xn + yn = zn в целых конечных числах, то есть имеются некие три числа, являющиеся гипотетическими решениями этого равенства. С другой стороны известно, что всегда можно вычислить сумму любых трех чисел. После безуспешных попыток вычислить сумму трех наших гипотетических чисел придем к выводу, что такая сумма не существует, а значит, не существуют и решения уравнения xn + yn = zn. Для большей убедительности приведем доказательство того, что сумма гипотетических чисел никак не может равняться какому либо конкретному числу и все, Великая теорема Ферма доказана.
Совершенно очевидно, что приведенное в этом примере доказательство неверно и даже просто абсурдно, но именно точно такую же схему доказательства предложил Фрей. Просто его рассуждения содержат не часто используемую терминологию, что позволяет удачно маскировать их абсурдность.
Впрочем, для гипотетически существующих трех чисел все же можно указать их сумму, но только в виде не реального числа, а гипотетически существующего числа. Точно также гипотетически существующей кривой Фрея может соответствовать только гипотетическая модулярная форма. И в принципе отсутствуют основания для существования у гипотетической кривой Фрея реальной модулярной формы. Да и гипотеза Таниямы не предусматривает рассмотрение гипотетических кубических уравнений и модулярных форм.
С другой стороны, если доказать, что коэффициенты a, b, c невозможно задать в качестве реально существующих чисел из-за отсутствия соответствующих решений для уравнения Ферма, то зачем доказывать что-то еще? Разве именно не это требовалось для доказательства Великой теоремы Ферма? А именно отсутствие соответствующих решений для уравнения Ферма. И в этом случае гипотеза Таниямы опять оказывается никак не связанной с Великой теоремой Ферма.
По этим причинам рассуждения Фрея выглядят не совсем корректными. Тем не менее, американский математик Кен Рибет обосновывает, что гипотетической кривой Фрея никак не может соответствовать какая-либо модулярная форма. То есть фактически обосновал, что если эллиптическая кривая не существует, то не существует и соответствующая ей модулярная форма. Впрочем, разве и безо всяких доказательств не является очевидным, что если нет конкретной эллиптической кривой, то нет и соответствующей ей модулярной формы?
Однако если не обращать внимания на эти проблемы, то для доказательства Великой теоремы Ферма осталось только обосновать гипотезу Таниямы. И в 1986 году англичанин Эндрю Уайлс, который с детства мечтал доказать Великую теорему Ферма и очень кстати ранее специализировался на теории эллиптических кривых, решился приступить к обоснованию гипотезы Таниямы.
Необходимо отметить, что доказательство гипотезы Таниямы вовсе не было легкой задачей. Достаточно сказать, что до Уайлса ее обоснование безуспешно пытались получить многие математики на протяжении тридцати лет.
После анализа проблемы Уайлс установил, что все множество эллиптических кривых распадается на некоторое семейство классов, существенно различающихся по своим свойствам. Каждый из этих классов требовал разработки специальных методов исследования. И вся эта работа требовала значительных затрат времени. Поэтому, опасаясь, что его обойдут возможные конкуренты, Уайлс проводил свои исследования в строжайшей тайне.
Только после нескольких лет напряженной работы, 23 июня 1993 года на Международной математической конференции в Кембридже Эндрю Уайлс наконец выступает с большой лекцией, в ходе которой он приводит обоснование гипотезы Таниямы и заявляет о доказательстве Великой теоремы Ферма.
Перед опубликованием в авторитетном математическом журнале, в соответствии с завещанием Пауля Вольфскеля, доказательство Уайлса объемом около двух сот страниц было поделено на шесть частей и передано на рецензирование различным ведущим математикам. И вскоре Ник Катц, один из рецензентов, в своей части доказательства Уайлса обнаруживает положение, которое не могло быть признано достаточно обоснованным. В результате представленное доказательство гипотезы Таниямы уже не могло считаться корректным. Но Эндрю Уайлису за сравнительно короткое время при помощи своего бывшего аспиранта Ричарда Тейлора все же удается закрыть пробел в своем доказательстве и 23 октября 1994 года представить в журнал доработанный вариант доказательства на ста тридцати страницах.
После тщательной проверки скорректированное доказательство Уйлса было признано безупречным и в мае 1995 года официально опубликовано [10, 11]. При этом вызывает удивление, что доказательство Уйлса было признанно корректным без ответов на имеющиеся очевидные проблемы в этом доказательстве. Совершенно непонятно как можно было в ходе тщательной проверки доказательства не заметить отмеченных выше проблем. Иначе как мистикой все это не объяснить.
Да доказательство Уйлса было принято большинством математиков, но все же не всеми. Ряд возражений было даже опубликовано, например [12, 13]. Но на эти возражения совершенно необъяснимым образом упорно продолжают не обращать внимание.
Еще в большей степени трудно объяснить, что Эндрю Уайлс, обосновавший только гипотезу Таниямы был признан автором доказательства Великой теоремы Ферма. Ведь очень хорошо известно, что любое правильное доказательство математической теоремы должно быть абсолютным относительно времени создания. Иначе говоря, не зависеть и признаваться в качестве доказательства независимо от времени получения. В случае с доказательством, предложенным Эндрю Уайлсем, это условие не выполняется. Действительно если бы Эндрю Уайлс доказал бы гипотезу Таниямы до получения Герхардом Фреем вывода о возможной связи гипотезы Таниямы с Великой теоремой Ферма, то был бы он признан автором доказательства Великой теоремы Ферма? Очевидно, что нет. С другой стороны, если кто-либо в будущем предложит доказательство гипотезы Таниямы отличное от доказательства Уайлса, то будет ли он считаться автором нового варианта доказательства Великой теоремы Ферма? Тоже очевидно, что нет.
И вообще, разве мало было получено различных математических утверждений, которые необходимо было использовать для доказательства Великой теоремы Ферма? Авторы всех этих математических утверждений тоже доказали Великую теорему Ферма?
Если рассуждения Герхарда Фрея считать корректными, то автором доказательства Великой теоремы Ферма логичнее было бы признать именно его, возможно в соавторстве с Кеном Рибетом.
Отмеченные проблемы в доказательстве Фрея – Рибета – Уайлса столь элементарны, что для того чтобы их понять, вовсе не надо быть профессиональным математиком. Поэтому совершенно непонятно чем все это можно объяснить?
Правда существуют утверждения, что современная математика вступила в эру слишком сложных, малопонятных большинству математиков доказательств. Доказательство Уайлса не стало исключением, действительно оно очень объемно и слишком сложно для понимания и, к сожалению явно не является тем чудесным доказательством, о котором говорил Пьер де Ферма. В связи с этим требовалось согласие математического сообщества с тем, что теорема на самом деле доказана.
В случае доказательства Великой теоремы Ферма, представленного Уайлсом, лишь совсем небольшое число специалистов по теории чисел признавали, что полностью понимают его рассуждения, а остальные просто сочли доказательство правильным. Те, кто не смог до конца понять доказательства, приняли его потому, что доказательство признали другие—те, кто все понял, и не захотели тратить свое время на то чтобы шаг за шагом проследить весь ход доказательства и проверить каждую деталь. При этом трудно сказать, сколько из тех немногих специалистов, которые считали, что полностью поняли доказательство, искренне не заблуждались на этот счет. Ведь даже при рецензировании текст доказательства был поделен на части, и каждый рецензент проверял только свою часть доказательства и не воспринимал его целиком [9].
И есть еще один вопрос. Рецензенты проверяли доказательство Великой теоремы Ферма или гипотезы Таниямы? Судя по всему, все же проверяли доказательство гипотезы Таниямы. А кто же тогда проверял доказательство Великой теоремы Ферма? Это обстоятельство отчасти способно объяснить существование отмеченных проблем доказательства Уайлса.
Однако ссылки на большие объемы и сложность современных доказательств не всегда оправданы. В большинстве случаев доказательства могут быть поделены на части, каждая из которых будет представлять собой совершенно самостоятельную теорему. Так, например, в состав доказательства Великой теоремы Ферма вовсе нет никакой необходимости включать доказательство гипотезы Таниямы, так как она является самостоятельной теоремой и может использоваться в ходе доказательства Великой теоремы Ферма наряду с другими существующими математическими утверждениями.
Кроме этого Великая теорема Ферма имеет особенности, которые позволяют осуществить проверку ее доказательств [4]. Уравнение xn + yn = zn для степени n = 2 имеет решения в целых конечных числах и для любых значений показателя степени n имеет решения в бесконечных целых числах. Однако из доказательства Фрея – Рибета – Уайлса вовсе не следуют эти исключения, а это указывает на возможную ошибочность предложенного доказательства или, как минимум, на его некорректность.
Решение проблемы Ферма связанной с его Великой теоремой заключается не только в отыскании любого доказательства этой теоремы, но и в ответе на вопрос мог или не мог Пьер де Ферма располагать доказательством в семнадцатом веке. Иначе говоря решить проблему Ферма это значит либо представить доказательство его теоремы основанное на математических методах доступных в семнадцатом веке, либо привести обоснование того, что доказать Великую теорему Ферма используя только математические методы семнадцатого века невозможно. Ведь не было выявлено принципиальных запретов на то, чтобы существовало доказательство Великой теоремы Ферма более простое, естественное и непротиворечивое, чем предложенное Фреем и Уайлисом.
Считается, что само по себе уравнение xn + yn = zn для показателя степени n большего двух не имеет большого значения для математики. Зато попытки доказательства Великой теоремы Ферма стимулировали развитие диофантового анализа, исследующего целые решения диофантовых уравнений, теории алгебраических чисел, теории идеалов, алгебраической геометрии и математики в целом в связи с открытием новых методов, обогативших многие смежные области математики. Наконец именно желание доказать Великую теорему Ферма ускорило получение Эндрю Уайлсом обоснования гипотезы Таниямы. Отыскание же утраченного доказательства самого Ферма ничего не даст кроме удовлетворения тщеславия человека решившего проблему Ферма.
Однако это не совсем так. Достаточно сказать, что восстановление доказательства Ферма способно повлиять на решение десятой проблемы Гильберта, предполагающей разработку метода позволяющего ответить на вопрос, будет ли диофантово уравнение общего вида иметь решение. И отрицательное решение Юрия Матиясевича десятой проблемы Гильберта [8] возможно стало бы можно пересмотреть. Несомненно, и на многие другие проблемы математики можно было бы посмотреть с совершенно иной стороны.
Если, несмотря на имеющиеся возражения, все же признать доказательство Эндрю Уайлса корректным, то необходимо учитывать, что Уайлс в своем доказательстве опирался на относительно слабо используемую на практике теорию арифметической алгебраической геометрии и ряд современных математических инструментов, созданных большим числом математиков за примерно последние сто лет, которые отсутствовали во время жизни Пьера де Ферма. В результате он получил доказательство очень объемное (в журнальном варианте занимает 120 страниц) и сложное для понимания даже профессиональными математиками, выполненное методами недоступными во время жизни Пьера де Ферма.
Как следствие этого реакция на представленное Эндрю Уайлсом косвенное доказательство была весьма нейтральной, сдержанной даже среди математического сообщества. Ведь, кроме того, что доказательство было необычайно сложным, а значит и трудно поддающимся надежной проверке, все ждали совсем иного доказательства, во всяком случае, полученного не любой ценой. Все дело в том, что Великая теорема Ферма приобрела столь большую популярность во многом благодаря сделанной Пьером де Ферма вместе с формулировкой теоремы на полях перевода «Арифметики» Диофанта записи: «Я нашел этому поистине чудесное доказательство, но поля здесь слишком узки, чтобы вместить его». И естественно ожидалось доказательство, выполненное элементарными методами доступными во время жизни Пьера де Ферма, которое сможет в первую очередь оказать влияние на развитие диофантового анализа.
Правда, сторонники доказательства Уайлса пытаются всех убедить в том, что методологическая сложность присуща всем великим доказательствам последнего времени и в дальнейшем будет только нарастать, что Пьер де Ферма ошибался, утверждая, что нашел доказательство своей теоремы, так как доказать ее методами отличными от методов Уайлса якобы невозможно по причине минимальности математических инструментов Уайлса. Вот только о какой минимальности математических инструментов Уайлса можно говорить, если его доказательство является косвенным?
Однако очевидно, что методы Уайлса Пьер де Ферма точно не мог использовать, но тогда какие методы он применил? На что могли несколько веков математики один за другим не обращать внимания? Что прекратили использовать, изменили или не стали развивать в математике?
К сожалению, склонность Ферма к мистификациям и подшучиваниям максимально осложнила получение ответов на эти вопросы. Достаточно вспомнить, сколько усилий было затрачено, на безуспешные попытки обобщить доказательство частного случая Великой теоремы Ферма для показателя степени n = 4 методом бесконечного спуска. А ведь было известно, что Ферма принципиально умалчивал о своих доказательствах. А тут вдруг взял и оставил доказательство для частного случая теоремы, а гораздо более важное доказательство общего случая не привел. И все равно вначале все сосредоточились именно на этом тупиковом методе доказательства строго в соответствии с направлением указанным Ферма. Получается, шутка Пьера де Ферма в очередной раз удалась?
Отмеченные в ходе анализа формулировки Великой теоремы Ферма, содержащиеся в ней неточности и неопределенности, явно умышленно привнесенные Пьером де Ферма, указывают на наличие иных подходов, отличных от подходов, использованных Эндрю Уайлсом, при доказательстве этой теоремы.
Так то, что уравнение xn + yn = zn для показателя степени n большего двух не имеет решений не только в конечных целых числах, но не имеет решений и в конечных дробях в сочетании с существующим методом преобразования любых конечных чисел, являющихся решениями данного уравнения в бесконечную последовательность новых решений указывает на то, что если бы такие решения существовали, то их было бы бесконечно много, и они были бы равномерно распределены, как среди маленьких чисел, так и среди очень больших чисел.
В Приложении 5 приведена таблица примеров решений уравнения x2 + y2 = z2 в конечных числах на интервале от 0,03 до 5. Приведенные в таблице решения составляют лишь ничтожно малую часть от общего количества существующих решений. Ведь на интервале от 0,03 до 5 существует бесконечно большое количество решений уравнения x2 + y2 = z2 в конечных числах.
Тут необходимо отметить, что ряды подобных решений уравнения вида xn + yn = zn практически можно получить только в том случае, если известно хотя бы одно решение данного уравнения в конечных числах. Поскольку подобных решений до сих пор обнаружено не было, то исследовалось уравнение с показателем степени n = 2. Для такого уравнения решения в конечных числах известны. Это пифагоровы тройки. Но если бы были известны решения в конечных числах для показателя степени n большего 2, то принципиально свойства решений для того уравнения не изменились бы.
Однако, к сожалению, возможность существования бесконечно большого количества решений уравнения вида xn + yn = zn, как среди маленьких чисел, так и среди очень больших чисел не позволяет обеспечить получения строгого доказательства Великой теоремы Ферма. Прежде всего, это связано с тем, что показатель степени n может быть бесконечно большим, а, следовательно, осуществить проверку для всех возможных значений показателя степени n физически невозможно. И с другой стороны, с каким бы шагом не проверялись возможные решения данного уравнения, всегда будет оставаться некоторая вероятность того, что при несколько ином шаге проверки возможных решений их все же удастся обнаружить.
Эти проблемы принципиально устранить невозможно. Поэтому не нахождение среди некоторого количества конечных чисел, принадлежащих некоторому интервалу решений уравнения вида xn + yn = zn, ничего не подтверждает и не опровергает.
При большом объеме проверенных конечных чисел, как и в случае использования компьютера, можно лишь вести речь о получении дополнительного обоснования гипотезы Великой теоремы Ферма.
И все же, часть бесконечного количества решений (если они, конечно, вообще существуют) уравнения вида xn + yn = zn в конечных числах всегда будет принадлежать ряду натуральных чисел. Это обстоятельство позволяет предположить существование возможной связи между наличием решений в конечных числах у уравнений рассматриваемого вида и свойствами ряда натуральных чисел. Но тогда во время жизни Пьера де Ферма должен был существовать метод анализа свойств ряда натуральных чисел, который позже перестал использоваться в математике. И такой метод действительно был – это методика нумерологического исследования чисел.
В настоящее время нумерологию относят к лженаукам или паранаукам со всеми вытекающими из этого обстоятельства последствиями. Но при жизни Пьера де Ферма нумерология вовсе не считалась лженаукой и никаких предубеждений против использования методов нумерологии, в том числе и в математике, не существовало.
Нумерология, как учение, возникла и полностью сформировалась, задолго до рождения Ферма и поэтому он мог быть знаком с ее методами.
Вообще невозможно точно установить, когда именно зародилась нумерология, в связи с тем, что в древности (в Вавилоне, Индии, Египте, Греции и Риме) она не отделялась от философии и математики. Хотя можно предположить, что Ферма вероятнее всего мог использовать положения варианта, так называемой, западной нумерологии, которые были разработаны еще в шестом веке до нашей эры древнегреческим философом и математиком Пифагором.
Конечно, речь не идет о применении Пьером де Ферма нумерологии, как таковой, как системы вероятностных связей между числами и различными объектами материального мира и временными событиями. Речь идет об использовании чисто математических представлений Пифагора о возможности сокращения любого числа до цифр от 1 до 9 включительно и рассматривании этих цифр в качестве исходных, из которых могут быть получены все другие числа.
Для выполнения нумерологического сокращения чисел были разработаны разные системы. Самый простой и популярный метод - сложить все цифры рассматриваемого числа, затем, если получается десять или более, сложить и эти цифры. Этот процесс продолжают до тех пор, пока не получат какую либо цифру от 1 до 9.
С позиции классической математики вся эта процедура является абсолютно бессмысленной, и получаемые в результате ее выполнения результаты никак не могут быть использованы в дальнейших чисто математических исследованиях.
Тем не менее, нумерологическое сокращение чисел продолжают использовать до сих пор, правда, исключительно для составления нумерологических прогнозов. Долгое время нумерологическое сокращение чисел существовало только в виде алгоритма, что не способствовало пониманию математической сути данного действия. Однако весь этот алгоритм можно представить в виде всего одной формулы [15], а ее анализ наглядно показывает, что нумерологическое сокращение чисел оказывается, вовсе не является с позиции математики таким уж бессмысленным.
Составить уравнение, задающее функцию нумерологического сокращения чисел можно несколькими способами. Например, можно просто взять и записать в виде формулы алгоритм сокращения чисел, используемый еще Пифагором. Тогда будет получено следующее уравнение:
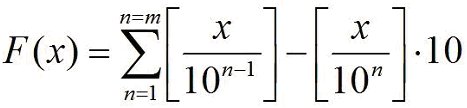
где x – значение нумерологически сокращаемого числа; m – количество цифр в числе x; [ ] – знак обозначающий целую часть числа или обозначает операцию по отбрасыванию дробной части от результата вычисления выражения, стоящего в прямоугольных скобках.
Недостатком данного уравнения является то, что оно неполное и не может нормально использоваться без введения дополнительных словесных пояснений. Так в случае, если при выполнении вычислений с его использованием будет получено двухзначное и более число, то все вычисления придется повторить, но уже, с полученным в ходе предыдущего применения уравнения, числом. Конечно, рассматриваемое уравнение можно дополнить выражениями, которые позволят отказаться от использования словесных пояснений, и результат будет получаться в ходе прямых и непрерывных вычислений, но в любом случае такое уравнение будет слишком громоздким и сложным.
Другой способ получения уравнения нумерологического сокращения чисел основывается на утверждении [16], что математически процедура нумерологического сокращения числа эквивалентна делению этого числа по некоторому модулю. Для целей нумерологии модуль наиболее часто имеет значение – 9, но может принимать и иные значения. Или, если говорить иначе, процедура нумерологического сокращения числа эквивалентна замене исходного числа его остатком от целочисленного деления на 9.
Таким образом, предполагается, что процедура нумерологического сокращения числа может быть описана методами арифметики вычетов, которую часто еще называют модульной арифметикой или модулярной арифметикой. В Приложении 6 приведены основные положения арифметики вычетов.
Соответственно формула нумерологического сокращения чисел на основе арифметики вычетов сведется к математическому выражению очень простого вида:
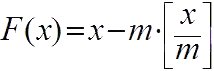
где x – значение нумерологически сокращаемого натурального числа; m – модуль (для целей нумерологии наиболее часто имеет значение – 9); [ ] – знак обозначающий целую часть числа или обозначает операцию по отбрасыванию дробной части от результата вычисления выражения, стоящего в прямоугольных скобках.
Данная формула задает периодическую импульсную функцию [21].
С другой стороны эта формула выполняет процедуру замены исходного числа его остатком от целочисленного деления на модуль. Необходимо отметить, что в арифметике вычетов эту процедуру по непонятным причинам предпочитают задавать не в виде формулы, а словесными формулировками. Между тем рассматриваемая формула очень наглядно показывает ошибочность утверждения, что математически процедура нумерологического сокращения числа эквивалентна делению этого числа по некоторому модулю. А вот при использовании только словесных формулировок ошибка становится уже не столь заметной.
Так, возьмем, например, число 17 и сократим его обычным, принятым в современной нумерологии методом, то есть сложим цифры 1 и 7. В результате получим 8. Теперь разделим 17 на модуль 9 и мы увидим, что остатком от этого целочисленного деления будет тоже число 8. Получается, что рассматриваемое математическое утверждение вроде бы верно. Возможно, именно подобные примеры способствовали распространению ошибочного утверждения. Однако анализ полученной формулы сразу покажет, что остатком от деления на модуль всех чисел кратных модулю всегда будет ноль. Но при нумерологическом сокращении любого числа, то есть вычислении суммы всех цифр составляющих число ноль получить в принципе невозможно.
Например, возьмем число 18 кратное 9. 1+8=9, то есть нумерологически число 18 сокращается до 9. Теперь 18/9 = 2, то есть 18 делится на 9 без остатка или остаток от этого деления равен 0, а вовсе не 9, как это должно быть согласно, рассматриваемого нами математического утверждения.
То, что рассматриваемая формула выполняет процедуру замены исходного числа его остатком от целочисленного деления на модуль m и тем самым задает периодическую импульсную функцию, показывает очевидность возможности преобразования с помощью этой формулы ряда натуральных чисел в бесконечно повторяющуюся последовательность чисел следующего вида: 1, 2, …, m – 1, 0, 1, 2, …, m – 1, 0, …. Пример такого преобразования представлен в следующей таблице:
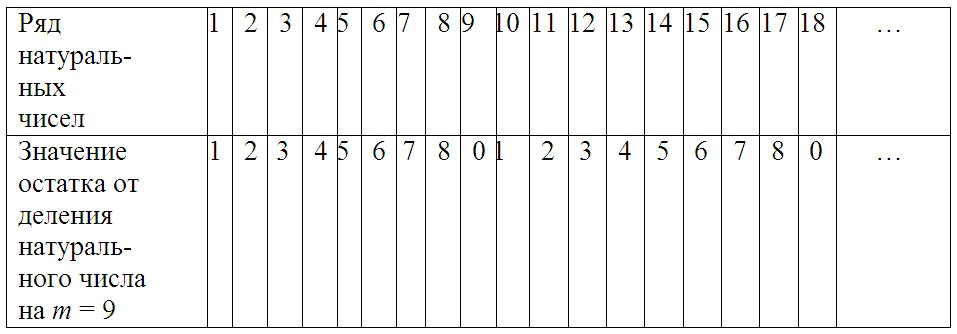
В теории сравнений предусмотрена возможность разбиения множества натуральных чисел на m групп относительно m, в которых элементы одной и той же группы будут иметь одинаковые вычеты по модулю m. Но и только. А вот возможность преобразования ряда натуральных чисел в ряд вида: 1, 2, …, m – 1, 0, 1, 2, …, m – 1, 0, … не рассматривается. Соответственно из теории сравнений было исключено нумерологическое положение Пифагора о рассматривании цифр от 1 до 9 в качестве исходных, из которых могут быть получены все остальные числа. То есть преобразование ряда: 1, 2, …, m – 1, 0, 1, 2, …, m – 1, 0, … обратно в ряд натуральных чисел даже не рассматривалось.
И это неудивительно, так как в ряде: 1, 2, …, m – 1, 0, 1, 2, …, m – 1, 0, … систематически появляется ноль, который препятствует получению достаточно элементарной и очевидной формулы преобразования этого ряда в ряд натуральных чисел. А вот при выполнении процедуры нумерологического сокращения чисел подобная проблема не может даже возникнуть.
Таким образом, получается, что арифметика вычетов и нумерологическое сокращение чисел являются разными математическими процедурами и арифметика вычетов никак не может заменить нумерологическое сокращение чисел.
То, что столь очевидная ошибка упорно на протяжении длительного времени не замечается само по себе удивительно и необъяснимо. Но еще большее удивление вызывает то обстоятельство, что она продолжает ряд непосредственно связанных, с Великой теоремой Ферма странностей (неточностей, ошибок) в ее формулировке, доказательстве Уайлеса и целом ряде выводов полученных при многочисленных попытках доказать эту теорему. На них обращалось внимание, когда приводился анализ формулировки Великой теоремы Ферма и попыток ее доказательства. Очень странным является не только их большое количество, но и их очевидность и соответственно простота обнаружения. Но, несмотря на это, они продолжают существовать, и исправлять их никто похоже не собирается.
То есть имеются основания утверждать, что к мистификации Великой теоремы Ферма причастен не только сам Пьер де Ферма, но ее мистификации так же уж вольно или не вольно, но способствовали многочисленные поколения математиков.
Казалось бы, ничего не изменится, если будет признан факт несоответствия арифметики вычетов и нумерологического сокращения чисел. Тем более что частично результаты, получаемые от применения арифметики вычетов и нумерологического сокращения чисел, совпадают. Но это не совсем так.
Дело в том, что при выполнении нумерологического сокращения чисел удается избежать использования числа ноль, а при применении арифметики вычетов нет.
Избежать использования нуля в качестве самостоятельного числа желательно, так как по своим свойствам ноль резко отличается от всех прочих чисел. Вообще долгое время он рассматривался почти исключительно как математический знак, выражающий отсутствие значения данного разряда в записи числа в позиционной системе счисления. Так в Европе даже в семнадцатом веке ноль все еще преимущественно считался условным символом и не признавался числом.
Поэтому сомнительно чтобы Ферма при доказательстве своей теоремы мог опираться на арифметику вычетов в любой ее форме, так как она предусматривает обязательное использование нуля. Этим же обстоятельством частично можно объяснить указанные выше некоторые странности в составленной им формулировке его Великой теоремы.
И это вовсе неудивительно. Ведь охарактеризовать свойства нулевого отрезка (промежутка и тому подобных объектов) невозможно. Достаточно попробовать указать для таких объектов протяженность или ориентацию в пространстве, времени, чтобы понять это. В результате именно при использовании нуля чаще всего появляются математические выражения, значения которых определить невозможно.
Необходимо отметить, что встречаются высказывания, связанные, с так называемой, малой теоремой Ферма, в которых утверждается, что Ферма якобы в очередной раз опередил свое время и использовал теорию сравнений при формулировании данной теоремы. При этом про использованные им методы для ее доказательства вообще ничего сказать невозможно, так как свое доказательство он как обычно не опубликовал.
Однако понятие и символьные обозначения теории сравнений были введены Гауссом в его книге «Арифметические исследования», изданной в 1801 году через сто тридцать шесть лет после смерти Пьера де Ферма.
Возможно, подобные высказывания вызваны тем обстоятельством, что в современной формулировке малой теоремы Ферма обычно используются понятия и символьные обозначения теории сравнений [18]. Но ведь сам Пьер де Ферма ни этих понятий, ни этих символьных обозначений никогда не использовал.
Поскольку понятия и символьные обозначения теории сравнений были введены после смерти Пьера де Ферма, а сам он никаких определенных высказываний по поводу теории сравнений не делал, то все же логичнее будет предположить, что Ферма не знал, что нумерология является лженаукой и процедуру нумерологического сокращения числа следует заменить делением этого числа по некоторому модулю. И более того считать, что эти две процедуры дают абсолютно идентичные результаты.
Но если формулу, выполняющую процедуру замены исходного числа его остатком от целочисленного деления на модуль m дополнить выражениями, позволяющими в ходе выполнения вычислений ноль заменять значением выбранного модуля m, то можно получить полностью соответствующую процедуре нумерологического сокращения чисел формулу:
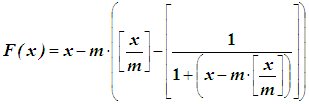
где x – значение нумерологически сокращаемого натурального числа; m – модуль; [ ] – знак, обозначающий целую часть числа или обозначает операцию по отбрасыванию дробной части от результата вычисления выражения, стоящего в прямоугольных скобках [15].
Данная формула так же задает периодическую импульсную функцию и позволяет преобразовывать ряд натуральных чисел в бесконечно повторяющуюся последовательность чисел следующего вида: 1, 2, …, m, 1, 2, …, m, …. То есть данная периодическая функция в пределах каждого своего периода последовательно принимает значения от 1 до m. При этом, как и в случае классического нумерологического сокращения чисел, появление в получающейся последовательности чисел нуля практически невозможно. Пример такого преобразования представлен в следующей таблице:
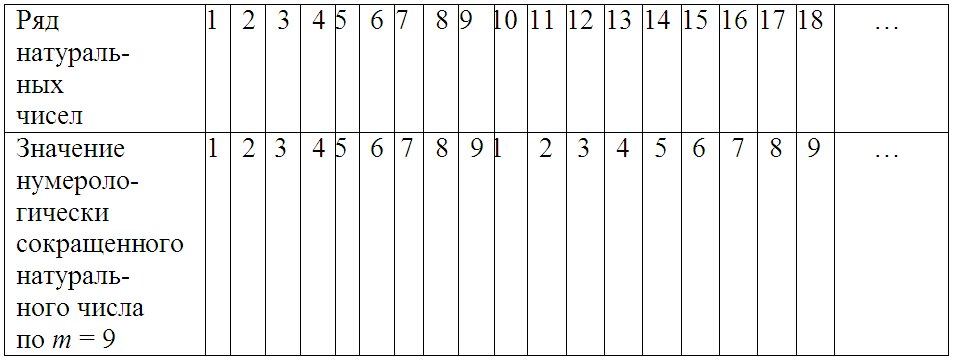
Необходимо отметить, что полученная формула, в отличие от представлений Пифагора о возможности сокращения любого числа до цифр от 1 до 9 включительно, указывает на возможность выполнения нумерологического сокращения от 1 до любого числа. Примеры таких сокращений чисел натурального ряда приведены в следующей таблице:
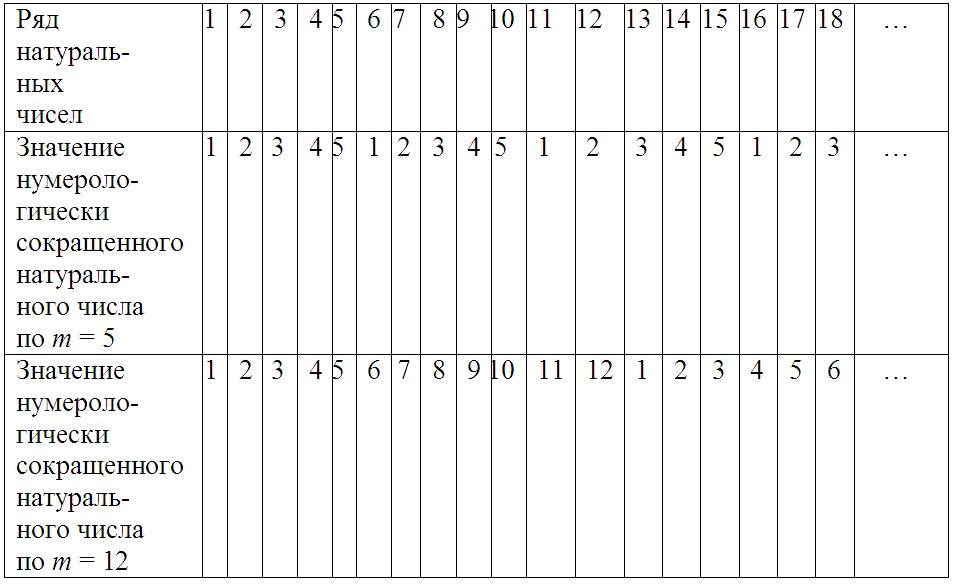
Кроме этого отсутствуют, какие либо проблемы с составлением формулы для преобразования числового ряда: 1, 2, …, m, 1, 2, …, m, …. в ряд натуральных чисел. Действительно она может быть записана в виде очень простого выражения:
A = m · N – m + F,
где A – исходное число до нумерологического сокращения; N – порядковый номер периода в числовом ряде: 1, 2, …, m, 1, 2, …, m, …. (Данный числовой ряд в пределах каждого своего периода последовательно принимает значения от 1 до m.); F – нумерологическое число из ряда 1, 2, …, m; m – модуль нумерологического сокращения числа.
Приведем пример применения данной формулы.
Допустим, необходимо узнать какое число A натурального ряда будет соответствовать нумерологическому числу F = 9 из периода N = 111 по модулю m = 9. Для этого подставляем F = 9, N = 111 и m = 9 в формулу и производим вычисления: А = 9 · 111 – 9 + 9 = 999
Проверяем, действительно ли, получившееся в ходе вычислений, число А = 999 нумерологически сокращается до F = 9: 9 + 9 + 9 = 27 (2 + 7 = 9).
Необходимо еще раз обратить внимание на то, что если бы число 999 сокращалось бы методами арифметики вычетов, то есть заменялось бы его остатком от целочисленного деления на модуль m = 9, то было бы получено значение нумерологического числа F не девять, а ноль. Такое изменение значения числа F в свою очередь приведет к вычислению при помощи рассматриваемой формулы неверного значения числа А = 9 · 111 – 9 + 0 = 990.
Таким образом, Пифагор был абсолютно прав, когда утверждал, что из ряда чисел от 1 до 9 могут быть получены все остальные числа натурального ряда. И Пьер де Ферма вполне мог опираться в своих доказательствах на это утверждение Пифагора. Единственное в чем был не совсем точен Пифагор, так это в том, что все числа натурального ряда могут быть получены не только из ряда чисел от 1 до 9, но и из любого подобного ряда чисел, а минимальный ряд таких чисел состоит всего из двух чисел – единицы и двойки.
Действительно, бесконечный числовой ряд: 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, …. при помощи рассмотренных формул преобразуется в бесконечный числовой ряд вида: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …., то есть фактически в натуральный ряд чисел. А вот числовой ряд, состоящий из одних единиц, уже не будет выражать периодическую функцию, и преобразовывать его станет невозможно.
Таким образом, является очевидным, что члены бесконечных числовых рядов 1, 2, …, m, 1, 2, …, m, …. и 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,… взаимно связаны, и один ряд может быть всегда преобразован в другой.
Поскольку нумерологическое сокращение осуществляется путем сложения всех цифр сокращаемого числа, то числа натурального ряда и соответствующие им нумерологические числа F (от 1 до m) будут показывать схожие свойства при совершении с ними в первую очередь операций сложения.
Это означает, что при выполнении операций сложения можно отказаться от непосредственного использования в ходе вычислений больших чисел и заменить большие числа, на числа F, получаемые при нумерологическом сокращении (фактически на числа от 1 до m) и при этом получить качественно (но не количественно) практически идентичный результат. Иначе говоря, все изменения свойств, полученные при выполнении операций сложения с числами F от 1 до m, могут быть распространены на все числа соответствующие этим числам F в ряду натуральных чисел.
К операциям сложения можно отнести не только собственно само сложение, но и операцию умножения, и операцию возведения в степень. Так как умножение можно заменить повторением операций сложения, например: 4 · 5 = 20 (4 + 4 + 4 + 4 + 4 = 20) или 33 = 27 3 · 3 · 3 = 27 (3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 27).
Великая теорема Ферма как раз и предполагает выполнение только операций сложения и возведения в степень. Поэтому для целей ее доказательства достаточно рассмотреть закономерности выполнения операций сложения с числами натурального ряда представленных с использованием соответствующих им нумерологических чисел F (от 1 до m).
Рассмотрим сложение двух произвольных чисел A1 = m · N1 – m + F1 и A2 = m · N2 – m + F2, представленных с использованием соответствующих им нумерологических чисел F.
A3 = A1 + A2 = m · (N1 + N2) – 2 · m + F1 + F2
Полученное выражение для вычисления суммы чисел A1 и A2 может быть приведено к виду: A3 = m · N3 – m + F3, где
N3 = N1 + N2 – 1 + [(F1 + F2) / (1 + m)],
где в свою очередь [ ] – знак обозначающий целую часть числа или обозначает операцию по отбрасыванию дробной части от результата вычисления выражения, стоящего в прямоугольных скобках; F3 – результат нумерологического сокращения суммы чисел F1 и F2 по модулю m.
Из выражения для вычисления значения A3 суммы чисел A1 и A2 следует, что не только результат F3 нумерологического сокращения числа A3 по модулю m в обязательном порядке должен быть равен результату нумерологического сокращения суммы чисел F1, F2,… Fk по тому же значению модуля m, но и порядковый номер периода N3 обязательно должен быть равен одному из следующих значений сумм: N1 + N2 + …+ Nk, N1 + N2 + …+ Nk – 1,… N1 + N2 + …+ Nk – (k – 1), где k – количество слагаемых в сумме A1 + A2 + ….
Поясним это утверждение при помощи конкретных числовых примеров.
Вычислим сумму трех произвольных чисел: 5 + 12 + 71 = 88. Теперь произведем нумерологическое сокращение, например, по модулю m = 7 каждого из этих чисел и определим соответствующие им номера периодов в бесконечной числовой последовательности 1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7,…. В результате для 5 получим F1 = 5 и N1 = 1, для 12 получим F2 = 5 и N2 = 2, для 71 получим F3 = 1 и N3 = 11 и для 88 получим F4 = 4 и N4 = 13.
Число 4, являющееся результатом нумерологического сокращения по модулю m = 7 суммы чисел F1 + F2 + F3 = 5 + 5 + 1 = 11 окажется равно F4 = 4. И это правило будет выполняться всегда независимо от количества слагаемых и способов выполнения сложения (тут имеются в виду операции умножения и возведения в степень).
А порядковый номер периода N4 = 13 = N1 + N2 + N3 – 1 = 1 + 2 + 11 – 1 = 13. Это правило будет так же выполняться всегда независимо от количества слагаемых. Правда, необходимо отметить, что возможное значение периода N все же в небольших пределах будет зависеть от количества слагаемых.
Поскольку бесконечный ряд натуральных чисел всегда может быть преобразован в бесконечный периодический числовой ряд 1, 2, …, m, 1, 2, …, m, …., то свойства чисел натурального ряда соответствующие числам ряда 1, 2, …, m, 1, 2, …, m, …. тоже периодически будут повторяться. Поэтому свойства чисел натурального ряда, соответствующие числам первого периода числового ряда 1, 2, …, m, 1, 2, …, m, …. будут бесконечно воспроизводиться в последующих периодах, а, следовательно, появляется возможность делать оценку свойств сумм чисел определенного вида на протяжении всего бесконечного ряда натуральных чисел. Числовой ряд 1, 2, …, m, 1, 2, …, m, …. в пределах каждого своего периода последовательно принимает значения от 1 до m.
Правда для того, чтобы такая оценка являлась корректной необходимо, чтобы количество чисел в периоде 1, 2, …, m числового ряда 1, 2, …, m, 1, 2, …, m, …. была равна числу слагаемых плюс единица. То есть модуль нумерологического сокращения m должен быть равен числу слагаемых плюс единица.
Кроме этого сумма чисел: 1 + 2 + …+ m – 1 не должна превосходить m.
Тогда для суммы двух слагаемых модуль нумерологического сокращения m должен быть равен трем и сумма 1 + 2 = 3 не будет превосходить m.
Для суммы трех слагаемых модуль нумерологического сокращения m должен быть равен четырем и сумма 1 + 2 + 3 = 6 уже будет превосходить m.
Для суммы четырех слагаемых модуль нумерологического сокращения m должен быть равен пяти и сумма 1 + 2 + 3 + 4 = 10 тоже будет превосходить m.
Очевидно, что и дальше с ростом числа слагаемых сумма чисел: 1 + 2 + …+ m – 1 всегда будет превосходить m.
Таким образом, получается, что корректная оценка возможна только для диофантовых уравнений, состоящих из двух слагамых. Нетрудно понять, с чем это связано – ведь любое количество слагаемых всегда можно представить в виде двух слагаемых. А вот меньшее число слагаемых существовать не может. Это удивительно, но диофантово уравнение xn + yn = zn как раз состоит из двух слагаемых.
Возможно, именно это обстоятельство имел в виду Пьер де Ферма, когда утверждал, что он нашел «поистине чудесное доказательство».
Теперь можно перейти к исследованию изменений свойств суммы xn + yn по мере изменений значения показателя степени n. Для этого составим таблицу, в которую последовательно занесем значения чисел A натурального ряда, начиная с единицы, результаты возведения чисел A в степень n, начиная с двух, результаты F нумерологического сокращения по модулю m = 3 чисел An и соответствующие числам An номера периодов N в бесконечной числовой последовательности 1, 2, 3, 1, 2, 3, 1, 2, ….
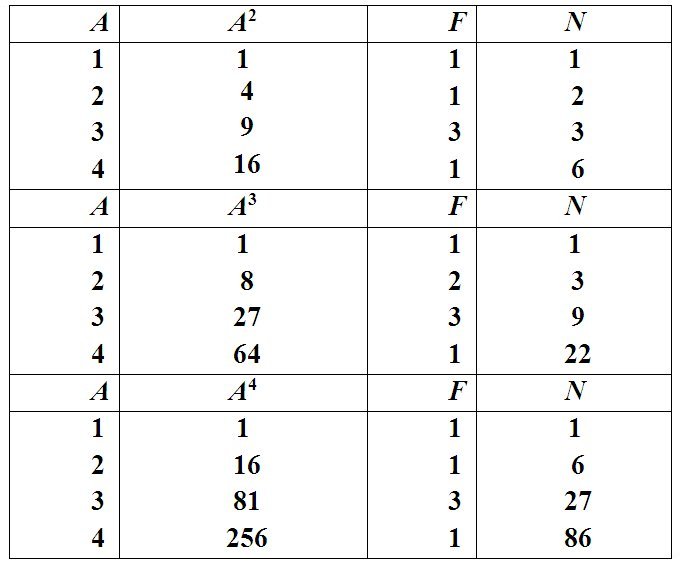
Возводя в степень последовательно члены A натурального ряда чисел можно получить все возможные значения слагаемых в уравнении xn + yn = zn. Однако в связи с тем, что ряд натуральных чисел бесконечен эти возможные значения слагаемых будут так же представлять собой бесконечный ряд чисел. Поэтому в таблице приведены значения соответствующие только началу натурального ряда чисел в объеме достаточном для оценки свойств чисел соответствующих первому периоду бесконечной числовой последовательности 1, 2, 3, 1, 2, 3, 1, 2, …., а так же в связи с тем, что свойства чисел первого периода будут бесконечно периодически повторяться.
Теперь при помощи таблицы проверим возможность существования решений в конечных целых числах у уравнения xn + yn = zn. Для этого проверим, выполняются ли для чисел 1n, 2n, 3n, соответствующих числам A – 1, 2, 3 выше отмеченные условия. А именно равенство результата F3 нумерологического сокращения одного из чисел An результату нумерологического сокращения суммы чисел F1 + F2, полученных при нумерологическом сокращении двух оставшихся чисел An при выполнении всех нумерологических сокращений по модулю m = 3 и равенство порядкового номера периода N3, либо N1 + N2, либо N1 + N2 – 1.
Так для случая, когда n = 2 (A2), если принять имеющиеся в таблице для первого периода бесконечной числовой последовательности 1, 2, 3, 1, 2, 3, 1, 2, …. значения F следующим образом: F1 = 1, F2 = 3, F3 = 1, то F1 + F2 = 1 + 3 = 4. Число 4, а значит и сумма F1 + F2 нумерологически по модулю m = 3 сокращается до 1, то есть нумерологически сокращенная сумма чисел F1 + F2 равна F3 = 1. Если принять имеющиеся в таблице для первого периода бесконечной числовой последовательности 1, 2, 3, 1, 2, 3, 1, 2, …. значения N следующим образом: N1 = 1, N2 = 2, N3 = 3, то N1 + N2 = 1 + 2 = 3 = N3.
Поскольку для значений A2 нумерологически сокращенные по модулю m = 3 F1 + F2 = F3 и N1 + N2 = N3, то уравнение x2 + y2 = z2 может иметь решения в конечных целых числах.
Необходимо отметить, что рассмотренная процедура оценки свойств уравнения xn + yn = zn позволяет лишь указать на возможность существования решений у данного уравнения, но не может подтвердить их реальное существование и не может указать их количество.
Для случая, когда n = 3 (A3), если принять имеющиеся в таблице для первого периода бесконечной числовой последовательности 1, 2, 3, 1, 2, 3, 1, 2, …. значения F следующим образом: F1 = 1, F2 = 2, F3 = 3, то F1 + F2 = 1 + 2 = 3 = F3. Если принять имеющиеся в таблице для первого периода бесконечной числовой последовательности 1, 2, 3, 1, 2, 3, 1, 2, …. значения N следующим образом: N1 = 1, N2 = 3, N3 = 9, то N3 = 9 значительно будет больше N1 + N2 = 1 + 3 = 4.
Поскольку для значений A3 хоть нумерологически сокращенные по модулю m = 3 F1 + F2 = F3, но при N3 значительно превышающем N1 + N2, уравнение x3 + y3 = z3 все же не будет иметь решений в конечных целых числах.
Для случая, когда n = 4 (A4), если принять имеющиеся в таблице для первого периода бесконечной числовой последовательности 1, 2, 3, 1, 2, 3, 1, 2, …. значения F следующим образом: F1 = 1, F2 = 3, F3 = 1, то F1 + F2 = 1 + 3 = 4. Число 4, а значит и сумма F1 + F2 нумерологически по модулю m = 3 сокращается до 1, то есть нумерологически сокращенная сумма чисел F1 + F2 равна F3 = 1. Если принять имеющиеся в таблице для первого периода бесконечной числовой последовательности 1, 2, 3, 1, 2, 3, 1, 2, …. значения N следующим образом: N1 = 1, N2 = 6, N3 = 27, то N3 = 27 значительно будет больше N1 + N2 = 1 + 6 = 7.
Поскольку для значений A4 хоть нумерологически сокращенные по модулю m = 3 F1 + F2 = F3, но при N3 значительно превышающем N1 + N2, уравнение x4 + y4 = z4 все же тоже не будет иметь решений в конечных целых числах.
И далее с ростом значения показателя степени n разница между N1 + N2 и N3 будет только увеличиваться, так как с ростом показателя степени n 3n растет быстрее, чем 1n + 2n. Таким образом, чем больше показатель степени n, тем больше будет отличаться результат возведения в степень числа 3 от суммы результатов возведения в ту же степень двух предыдущих чисел, а значит, и соответствующие этим числам значения N так же будут отличаться друг от друга во все большей степени. Следовательно, при любых показателях степени n больше двух уравнение xn + yn = zn не будет иметь решений в конечных целых числах.
Описанный здесь метод доказательства Великой теоремы Ферма выгодно отличается от многих предлагавшихся ранее тем, что позволяет объяснить существование решений в конечных целых числах у уравнения x2 + y2 = z2 не прибегая к известным способам доказательства теоремы Пифагора. И кроме этого существует достаточно очевидное объяснение того, почему данный метод не позволяет обнаружить решения уравнения xn + yn = zn в бесконечных целых числах. Все дело в том, что нумерологически сокращать можно только конечные числа, а вот бесконечные числа нельзя. Впрочем, методы арифметики вычетов к бесконечным числам так же применить невозможно.
Вообще, конечно, трудно объяснить, зачем потребовалось заменять более мощный математический инструмент нумерологического сокращения чисел на менее мощную арифметику вычетов. Ведь возможности, которые предоставляет арифметика вычетов при исследовании чисел, практически полностью могут быть реализованы в рамках нумерологического сокращения чисел. Правда, необходимо отметить, что преимущества нумерологического сокращения чисел, его более широкие возможности становятся очевидными только при описании его математическими формулами. А формулы эти удалось вывести на основе функций, которые были в общем виде опубликованы в самом конце двадцатого века, да и то в неспециализированном издании [22]. Причем для задания этих функций в свою очередь потребовалось использовать функции, введенные К. Гауссом в 1808 году, то есть спустя почти сто сорок лет после смерти Пьера де Ферма.
В связи с этим возникает вопрос, а мог ли Пьер де Ферма не гипотетически, а реально в доказательстве своей знаменитой теоремы опираться на методы нумерологического сокращения чисел и представления Пифагора о свойствах натурального ряда чисел? Действительно трудно поверить в то, что, не располагая аналитическим описанием этих методов, он смог разглядеть необходимые ему для доказательства закономерности. Но если вспомнить историю творчества Ферма, то придется согласиться с тем, что ему не раз очень многое удавалось разглядеть и, причем совершенно необъяснимым образом. Так почему и в случае со своей знаменитой теоремой он не мог в очередной раз продемонстрировать свои уникальные способности?
Применение исчерпывающих формул, не требующих значительных словесных пояснений во многом может облегчить решение задачи, и это было показано выше при анализе формулировки Великой теоремы Ферма при замене ее основного уравнения более однозначным уравнением, но составленным с использованием функций неизвестных во время жизни Ферма. Однако это не помешало сформулировать теорему не только самому Ферма, но и его куда более древним предшественникам.
Кроме этого Пьеру де Ферма вовсе не требовалось в своих доказательствах обосновывать все до последней запятой, так как он их никому не показывал и, соответственно, не подвергался критике, а это значит, что он мог довольствоваться лишь идеей доказательства, что ускоряло и одновременно упрощало его работу.
С другой стороны в настоящее время все равно больше не известно других математических методов кроме методов нумерологического сокращения чисел, которые были бы известны в семнадцатом веке и позволяли бы доказать Великую теорему Ферма. Кроме этого именно применение для доказательства теоремы этих методов никогда не пытались использовать, и это обстоятельство может объяснить, почему так долго не удавалось восстановить доказательство Ферма. И есть еще одно немаловажное обстоятельство. Именно нумерологическое сокращение чисел позволяет избежать использования нуля в качестве числа и таким образом обойти проблему того, что ноль в семнадцатом веке все еще не рассматривался в качестве числа и трудно представить, чтобы он в этом качестве мог применяться в ходе доказательства Великой теоремы Ферма.
Таким образом получается, что у Ферма все же имелась возможность доказать свою знаменитую теорему. В связи с этим совсем уже не обоснованными выглядят заявления о том, что Пьер де Ферма ошибался, утверждая, что нашел доказательство своей теоремы, так как доказать ее методами известными в семнадцатом веке якобы невозможно. Ведь нумерологическое сокращение чисел было известно уже несколько тысяч лет до семнадцатого века, и Пьер де Ферма по этой причине вполне мог назвать доказательство, основанное на столь древних методах «поистине чудесным доказательством». А его Великая теорема так и останется самым удачным математическим розыгрышем всех времен, так как с течением времени математики все больше утрачивают способность к восприятию и созданию подобных шуток. Очень трудно представить современного математика получившего доказательство трудной гипотезы и скрывшего его суть от своих коллег ради розыгрыша.
Приложение 1
1. Коммутативность: переместительные законы. Для любых чисел m и n
m + n = n + m и m·n = n·m.
2. Ассоциативность: сочетательные законы. Для любых чисел m, n и k
(m + n) + k = m + (n + k) и (m·n) ·k = m· (n·k).
3. Дистрибутивность: распределительный закон. Для любых чисел m, n и k
m· (n + k) = m·n + m·k.
4. Существует число 0, такое, что для любого числа n
n + 0 = n.
5. Существует число 1, такое, что для любого числа n
n ·1 = n.
6. Для любого числа n существует другое число k, такое, что
n + k = 0.
7. Для любых чисел m, n и k
если k ≠ 0 и k·n = k·m, то m = n.
Приложение 2
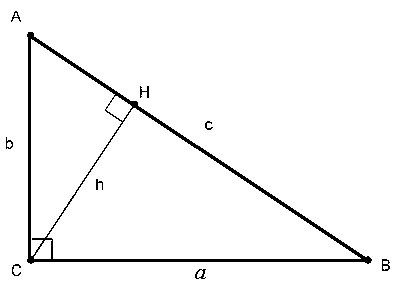
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведем высоту из C и обозначим ее основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения:
|BC| = a, |AC| = b, |AB| = c
получаем:
a/c = |HB|/a; b/c = |AH|/b,
что эквивалентно:
a2 = c·|HB|; b2 = c·|AH|.
Сложив, получаем:
a2 + b2 = c· (|HB| + |AH|) = c2 или a2 + b2 = c2, что и требовалось доказать. Существует большое количество доказательств теоремы Пифагора. С наиболее известными вариантами доказательств этой теоремы можно ознакомиться, например, в статье Г. Глейзер «О теореме Пифагора и способах ее доказательства» [2].
Приложение 3
Диофантово уравнение – это уравнение вида P(x1 , … , xn) = 0, где левая часть представляет собой многочлен от переменных x1 , … , xn с целыми коэффициентами. Любой упорядоченный набор (u1 ; … ; un) целых чисел со свойством P(u1 , … , un) = 0 называется частным решением диофантова уравнения P(x1 , … , xn) = 0. Решить диофантово уравнение это, значит, найти все его решения, или, как говорят, общее решение этого уравнения. Часто диофантовыми называют и уравнения вида P(x1 , … , xn) = Q(x1 , … , xn), где в левой и правой частях стоят многочлены от переменных x1 , … , xn : их всегда можно записать в виде диофантовых уравнений P(x1 , … , xn) – Q(x1 , … , xn) = 0.
Эти уравнения названы в честь Диофанта Александрийского. Через века до нашего времени дошли шесть книг из тринадцати его главного труда «Арифметика» и книга «О многоугольных числах». Он разрабатывал приемы нахождения рациональных решений алгебраических уравнений от нескольких неизвестных.
В качестве примеров диофантовых уравнений можно привести следующие уравнения:
3·x – 8 = 0 – диофантово уравнение первой степени от одной переменной x. Очевидно, что оно не имеет решений, так как 8 не делится нацело на 3. В то же время, это уравнение имеет корень, который не является целым числом.
Диофантово уравнение 6·x = 24 имеет единственное решение x = 4.
Диофантово уравнение x2 + y2 = z2 является уравнением из теоремы Пифагора и имеет бесконечно много решений в виде, так называемых, пифагоровых троек.
Диофантово уравнение xn + yn = zn при n > 2 согласно Великой теореме Ферма не имеет ненулевых решений в целых числах.
Уравнение xn + yn = zn Великой теоремы Ферма является предметом диофантова анализа.
Нахождение решений произвольных диофантовых уравнений – непростая задача. Более того, в семидесятых годах двадцатого века было доказано, что она алгоритмически неразрешима, то есть невозможно придумать алгоритм, который для произвольного заданного диофантова уравнения давал бы ответ на вопрос: «Есть у этого уравнения хотя бы одно решение?».
Приложение 4
Во исполнение воли д-ра Пауля Вольфскеля, скончавшегося в Дармштадте, мы объявляем о создании фонда в сто тысяч марок, каковая сумма и будет вручена тому, кто первым докажет Великую теорему Ферма.
Будут соблюдаться следующие правила.
1. Королевское научное общество в Гёттингене обладает полной свободой воли в принятии решения, кому надлежит присудить премию. Рукописи, представленные с единственной целью принять участие в конкурсе на получение премии, приниматься не будут. К рассмотрению допускаются только математические мемуары, представленные в виде статей в периодических изданиях или имеющиеся в книжных лавках. Общество обращается к авторам подобных мемуаров с просьбой присылать по крайней мере пять печатных экземпляров.
2. Работы, опубликованные на языках, непонятных ученым специалистам, выбранным для работы в жюри, не допускаются к участию в конкурсе. Авторам таких работ разрешается заменить их переводами, удостоверившись в точности последних.
3. Общество не берет на себя ответственность за рассмотрение работ, не представленных на конкурс, а также за ошибки, которые могут произойти из-за того, что автор работы или часть работы не известны Обществу.
4. Общество сохраняет за собой право принятия решения в случае, когда к решению проблемы имеет отношение несколько лиц или когда решение является результатом совместных усилий нескольких ученых, в том числе и по вопросам распределения премии.
5. Премия присуждается Обществом не ранее, чем через два года после опубликования мемуара, удостоенного премией. Двухлетний промежуток времени необходим для того, чтобы немецкие и иностранные математики имели возможность высказать свое мнение по поводу опубликованного решения.
6. После того, как состоится присуждение премии Обществом, секретарь от имени Общества уведомляет об этом лауреата. Решение публикуется всюду, где ранее было объявлено о конкурсе на соискание премии. Присуждение премии Обществом обсуждению не подлежит.
7. Выплата премии лауреату производится в течение трех месяцев после присуждения Королевским казначеем Гёттингенского университета или, на ответственность получателя, в любом указанном им месте.
8. Капитал может быть выплачен по желанию Общества под расписку либо наличными, либо переводом финансовых ценностей. Выплата премии считается произведенной при переводе этих финансовых ценностей даже в том случае, если к концу дня сумма премии не достигнет 100000 марок.
9. Если премия не будет присуждена до 13 сентября 2007 года, то дальнейшие заявки не принимаются.
Конкурс на соискание премии Вольфскеля считается открытым с сего дня на приведенных выше условиях.
Гёттинген, 27 июня 1908 г.,
Королевское общество наук
Приложение 5
|
x |
y |
z |
x2 + y2 |
z2 |
|
0,03 |
0,04 |
0,05 |
0,0025 |
0,0025 |
Приложение 6
Любое целое число a можно разделить с остатком на натуральное число m. Остаток от деления числа на m называется вычетом или если говорить строго вычетом числа a по модулю m. Операция, сопоставляющая числу a его вычет по модулю m, называется приведением a по модулю m.
Два целых числа a и b сравнимы по модулю m, если их разность делится на m. Числа, имеющие одинаковые остатки от деления на m, сравнимы по модулю m.
Значения вычетов по модулю m, принадлежат множеству 0, 1, …m-1. То есть целое число может иметь не больше, чем m остатков. Это значит, что множество целых чисел можно разбить на m групп относительно m. Элементы одной и той же группы будут иметь одинаковые вычеты по модулю m. Очевидно, что группы не пересекаются.
Наиболее часто в качестве примера использования в быту арифметики вычетов приводят обычные аналоговые часы. Когда говорят четыре часа по полудню, то имеют в виду, что после двенадцати часов дня прошло четыре часа, но принято называть не шестнадцать часов (12 + 4 = 16), а четыре часа. Это как раз и соответствует правилам арифметики вычетов по модулю 12, так как вычет числа 12 по модулю 12 равен 0, а вычет числа 16 по модулю 12 равен 4.
Данный пример наглядно демонстрирует суть арифметики вычетов, которая отрезает от числовой прямой участок по число равное модулю и соединяет конец этого участка с началом числовой прямой, то есть с нулем. Образуя, таким образом, из части числовой прямой числовое кольцо.
Более подробно с теорией сравнений можно ознакомиться, например, в [20].
1. Большой энциклопедический словарь / Ред. А.М. Прохоров. – 2-е изд., перераб. и доп . – М. : Большая Российская энциклопедия, 2000. – 1456 с.
2. Г. Глейзер. О теореме Пифагора и способах ее доказательства [Электронный ресурс]. – Интернет адрес: http://shenev.ru/ket/no24_01.htm
3. А.М. Белов. О доказательстве большой теоремы Ферма элементарными методами известными во время жизни Пьера де Ферма [Электронный ресурс]. – Интернет адрес: http://stob2.narod.ru/39s.htm, 2014.
4. А.М. Белов. Великая теорема Ферма неверна имеются ее решения среди бесконечных целых чисел теоретически доказать ее невозможно [Электронный ресурс]. – Интернет адрес: http://stob2.narod.ru/14s.htm, 2005.
5. Математика. Большой энциклопедический словарь/ Гл. ред. Ю.В. Прохоров. - 3-е изд. - М.: Большая Российская Энциклопедия, 2000. -848 с.
6. А.М. Белов. К вопросу детального математического описания уравнениями дискретных объектов и процессов [Электронный ресурс]. – Интернет адрес: http://stob2.narod.ru/20s.htm, 2006.
7. Эдвардс Г. Последняя теорема Ферма. Генетическое введение в алгебраическую теорию чисел.– М.: Мир, 1980.
8. Ю.В. Матиясевич. Десятая проблема Гильберта. — М.: Наука, 1993.
9. Сингх С. Великая теорема Ферма.– М.: МЦНМО, 2000.
10. Wiles A. Modular elliptic curves and Fermat's Last Theorem // Ann. of Math., 1995. – Vol. 142. – P. 443–551.
11. Taylor R., Wiles A. Ring-theoretic properties of certain Hecke algebras // Ann. of Math., 1995. – Vol. 142. – P. 553–572.
12. Ю.А. Ивлиев Ошибочное доказательство Уайлса Великой теоремы Ферма - Фундаментальные исследования (раздел «Физикоматематические науки») 2008 № 2, 13-16.
13. М.Б. Бабаев. О «доказательствах» проблемы, названной «Последняя теорема Ферма» [Электронный ресурс]. – Интернет адрес: http://evikaaz.narod.ru/m1.htm, 2005.
14. Абу Махмуд Хамид ибн ал-Хызр ал-Ходжанди: Биография [Электронный ресурс]. – Интернет адрес: http://people.su/119180.htm.
15. А.М. Белов. О нумерологии, лженауке, математике, формуле и калькуляторе нумерологического сокращения чисел [Электронный ресурс]. – Интернет адрес: http://stob2.narod.ru/36s.htm, 2013.
16. Нумерология [Электронный ресурс]. – Интернет адрес: https://ru.wikipedia.org/wiki/Нумерология.
17. Lucas N. H. Bunt, Phillip S. Jones, Jack D. Bedient The historical roots of elementary mathematics. — Courier Dover Publications, 1976.
18. Вилейтнер Г. История математики от Декарта до середины XIX столетия / пер. с нем. под. ред. А. П. Юшкевича. — М.: Физматлит, 1960.
19. В.Ф. Асмус Проблема интуиции в философии и математике Очерк истории: XVII – начало XX в. – М.: Соцэгиз, 1963.
20. И.М. Виноградов Основы теории чисел. – М.: Наука, 1972.
21. А.М. Белов. Периодические импульсные функции на основе универсального уравнения [Электронный ресурс]. – Интернет адрес: http://stob2.narod.ru/16s.htm, 2005.
22. А.М. Белов. Функция для описания скачкообразно и качественно изменяющихся процессов // Тульские ученые накануне третьего тысячелетия: Сб. аналит. и информ. материалов. - Тула: Гриф и Ко , 2000. - С. 40-41.