| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |

            В общем случае многоугольник представляет собой замкнутую ломаную линию. Обычно многоугольники описываются либо графически, либо словесными формулировками. Долгое время вообще не существовало математических уравнений описывающих такие многоугольники подобно уравнениям, определяющим окружность или эллипс. В 2003 году были предложены уравнения способные однозначно определять произвольный многоугольник в прямоугольных координатах (смотрите статью "Уравнения многоугольников и спиралей на их основе" http://stob2narod.ru/3s.htm). Причем каждый многоугольник описывался своим уравнением. Позже было установлено, что существует уравнение, способное описывать в полярных координатах все правильные выпуклые самонепересекающиеся многоугольники, а также выпуклые самопересекающиеся (звездчатые) правильные многоугольники.

            Многоугольник является выпуклым, если никакая сторона многоугольника, будучи неограниченно продолженной, не делит многоугольник на две части. Выпуклый многоугольник называется правильным, если все его стороны равны и все внутренние углы равны. Правильные выпуклые самопересекающиеся (звездчатые) многоугольники представляют собой многоугольники, у которых все стороны равны и каждая следующая из сторон повернута в одном и том же направлении на один и тот же угол по отношению к предыдущей, а их вершины лежат на одной окружности.

            Математическое уравнение способное задать любой из выше перечисленных правильных многоугольников в полярных координатах выглядит следующим образом:

            Полярные координаты определяются полярным радиусом R и полярным углом F и связаны с прямоугольными координатами X и Y формулами: X=R*CosF, Y=R*SinF.

            Обращаю внимание, что в уравнении (1) дальнейшие сокращения (например, сокращение 2 и 1/2) производить нельзя, так как в этом случае будет нарушен порядок вычислений и, соответственно, будет получен неверный результат.

            Как уже указывалось в пояснении к уравнению (1) коэффициент N в уравнении (1) определяет вид и количество сторон (вершин) многоугольника. Для всех N представленных целыми числами по величине большими двух уравнение (1) будет определять ряд правильных самонепересекающихся выпуклых многоугольников с числом сторон (вершин) равным N. Примеры, построенных при помощи уравнения (1), таких многоугольников приведены ниже в таблице:

            Для полного построения любого правильного самонепересекающегося выпуклого многоугольника необходимо и достаточно что бы полярный угол F изменялся в диапазоне от 0 до 2π . При бесконечно большом значении коэффициента N уравнение (1) фактически будет определять окружность.

            Для всех N представленных числами из ряда 2,5; 3,5; 4,5; 5,5; 6,5; 7,5; … (и так далее до бесконечности) уравнение (1) будет определять ряд выпуклых самопересекающихся (звездчатых) правильных многоугольников с нечетным количеством вершин равным 2N. Примеры, построенных при помощи уравнения (1), таких многоугольников приведены ниже в таблице:

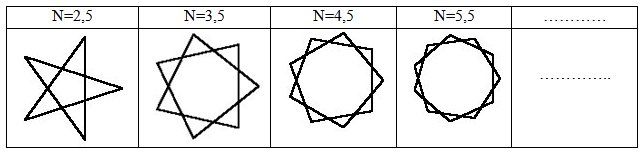
            Для полного построения любого самопересекающегося (звездчатого) правильного многоугольника с нечетным количеством вершин необходимо и достаточно что бы полярный угол F изменялся в диапазоне от 0 до 4π.

            Для всех N представленных числами с дробной частью по величине меньшей или большей 0,5 уравнение (1) будет определять неупорядоченный ряд многоугольников, примеры, которых приведены ниже в таблице:

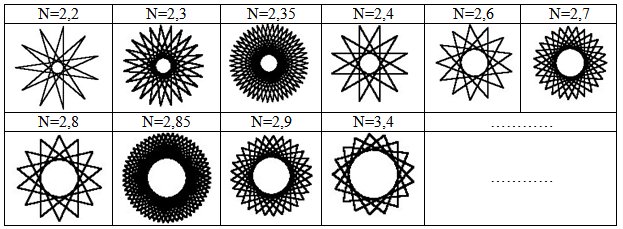
            Для полного построения таких многоугольников полярный угол F должен изменялся в диапазоне от 0 до величины превышающей 4π в зависимости от количества вершин многоугольника. Чем больше количество вершин, тем до большего значения должно изменяться максимальное значение полярного угла F. Количество вершин у таких многоугольников можно вычислить по следующему выражению: N/{N}, где {} – знак, обозначающий дробную часть числа N или {N}=N-[N].

            Для самостоятельного исследования свойств уравнения (1), особенно для тех, кто любит "все пощупать собственными руками", можно на форме в VisualBasic создать кнопку и загрузить в нее следующий код:

           
DrawWidth = 2
Rem Присваивание исходных значений переменным:
PI = 3.14159
L = 500
N = 4
For F = 0 To 6.28318 Step 0.001
Rem Код уравнения (1):
R = L / Cos(2 * PI / N * (1 / 2 * Fix(N * F / PI) - Fix(1 / 2 * Fix(N * F / PI))) - F + PI / N * Fix(N * F / PI))
Rem Перевод полярных координат в прямоугольные:
X = R * Cos(F)
Y = R * Sin(F)
Rem Вывод точек графика:
PSet (1.5 * X + 5000, 1.5 * Y + 5000)
Next F

            Данный код обеспечивает воспроизведение вычислений по уравнению (1) с построением графика по результатам вычислений. Разумеется, создав, таким образом, программу для исследования уравнения (1) вы сможете изменять в ней все, что угодно и сразу наблюдать результат своих действий. Кроме этого можно воспользоваться уже полностью готовой программой для исследования уравнения (1): http://stob2.narod.ru/yraw-praw-mnog/yraw-praw-mnog.exe или просто выполнить программу (сценарий) на языке JavaScript http://stob2.narod.ru/yraw-praw-mnog/script-mnog.htm построения правильных многоугольников непосредственно в окне обозревателя Интернет.

            Необходимо отметить, что JavaScript не предназначен для создания графических объектов и не имеет графического редактора. По этому графики на страницах обозревателя Интернета при помощи JavaScript создавались в текстовом редакторе, что привело к отображению многоугольников с небольшими искажениями и не позволяет строить многоугольники, требующие для этого большого объема вычислений. Хотя сам код сценария JavaScript и использованные для его написания приемы могут оказаться полезными сами по себе для желающих создавать графические объекты непосредственно в ходе выполнения сценариев JavaScript.

            Как видно из уравнения (1) полярный радиус R выражен через число π. Так как точное значение этого числа физически указать невозможно, то уравнение (1) реально обеспечивает лишь приближенное задание многоугольников. Правда, для практических нужд вместо числа π обычно бывает достаточным применения числа равного 3,14.

            Уравнение (1) представляет собой периодическую функцию, и все правильные многоугольники фактически определяются однотипными периодическими функциями. Это свойство уравнения (1) очень хорошо иллюстрирует приведенный ниже график:

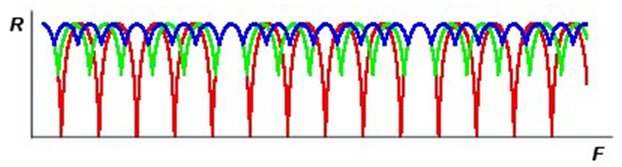
            На этом графике в прямоугольных координатах построены зависимости R от F по уравнению (1) соответственно для пятиконечного самопересекающегося многоугольника (красная линия на графике), равностороннего треугольника (зеленая линия на графике) и квадрата (синея линия на графике).

                                                                                                            август 2008 года