| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |

            В статье: "Уравнение правильных многоугольников в полярных координатах" (http://stob2narod.ru/27s.htm) приведено уравнение способное задавать (описывать) в полярных координатах практически любой правильный многоугольник, причем, как самонепересекающийся, так и самопересекающийся. Совершенно очевидно, что, располагая таким уравнением очень просто получить уравнения, задающие в полярных координатах различные спирали в виде многоугольников. Достаточно изменить уравнение правильных многоугольников в полярных координатах по аналогии с известными уравнениями спиралей для гладких функций, например, таких как параболическая спираль, плоская улитка, синусоидальная спираль, гиперболическая спираль, логарифмическая спираль и т. п. Далее приведен ряд примеров уравнений, задающих в полярных координатах спирали в виде многоугольников.

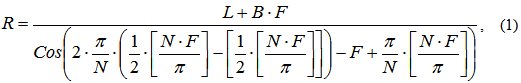
            где R – полярный радиус; F – полярный угол; L – коэффициент, может быть любым числом, физически представляет собой радиус окружности (для первого витка спирали) вписанной в многоугольник формирующий спираль; N – коэффициент, может быть любым числом, от его значения зависит вид, количество сторон (вершин) многоугольника формирующего спираль; B – коэффициент, определяющий расстояние между витками спирали; π - число пи, равное 3,14159…; [ ] – знак, обозначающий целую часть числа и предусматривающий отбрасывание дробной части от результата вычисления выражения, стоящего в скобках [ ]. Полярные координаты определяются полярным радиусом R и полярным углом F и связаны с прямоугольными координатами X и Y формулами: X=R*CosF, Y=R*SinF.

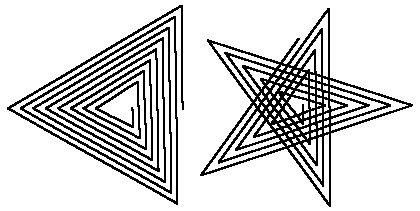
            Графики уравнения (1) представляют собой спирали, примеры которых, приведены ниже на рисунке соответственно для самонепересекающегося многоугольника (N=3) и самопересекающегося многоугольника (N =2,5).

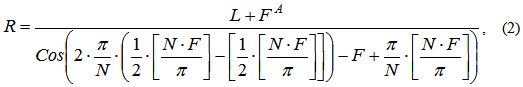
            где A – показатель степени, определяющий изменение величины шага спирали.

            Примеры спиралей, которые можно задать при помощи уравнения (2) приведены на рисунке ниже, построенные соответственно при A =2 для N=4 и N=4,71.

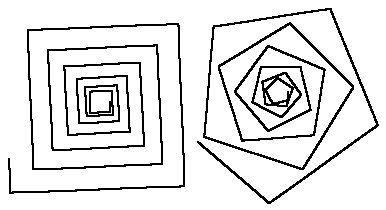
            При A<1 для N=5 и N=7,1 соответственно:

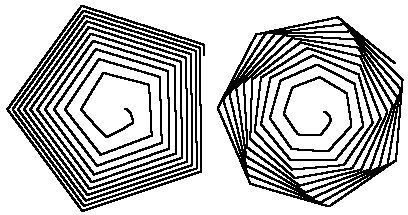
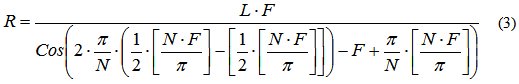
            Примеры спиралей, которые можно задать при помощи уравнения (3) приведены на рисунке ниже, построенные соответственно для N=7 и N=6,5.

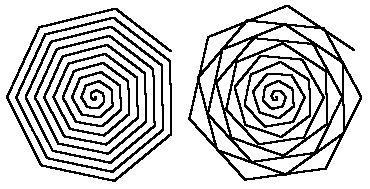
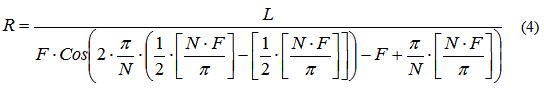
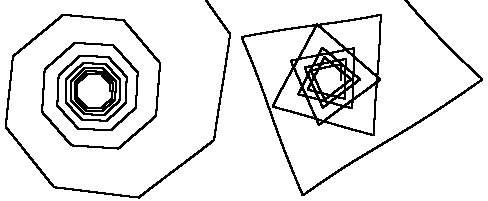
            Примеры спиралей, которые можно задать при помощи уравнения (4) приведены на рисунке ниже, построенные соответственно для N=8 и N=3,5.

            Поэкспериментировать с построением спиралей на основе предложенных уравнений можно выполнив программу (сценарий) на языке JavaScript http://stob2.narod.ru/yraw-spir-mnog/script-spir-mnog.htm построения спиралей в виде многоугольников непосредственно в окне обозревателя Интернет.

            Необходимо отметить, что JavaScript не предназначен для создания графических объектов и не имеет графического редактора. По этому графики на страницах обозревателя Интернета при помощи JavaScript создавались в текстовом редакторе, что привело к отображению спиралей с небольшими искажениями и не позволяет строить спирали, требующие для этого большого объема вычислений.

                                                                                                            сентябрь 2008 года