
Рис. 1
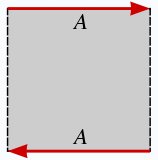
Рис. 2
| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
Лист Мебиуса (или лента Мебиуса, петля? Мебиуса, Mobius strip ) (Рис. 1) - трехмерная односторонняя поверхность, имеющая только одну сторону и одну границу, обладающая математическим свойством неориентируемости. Считается простейшей неориентируемой поверхностью с краем. Возможно, что простейшей односторонней поверхностью лист Мебиуса считается из-за простоты изготовления его модели. Ведь для получения листа Мебиуса необходимо совместить два конца достаточно длинной полоски так, чтобы направления красных стрелок "А" (см. Рис. 2) совпали, превратив полоску в замкнутую фигуру, то есть соединить концы полоски, предварительно перевернув один из них вполоборота (на 180 градусов). Кажется, что ничего проще этой процедуры быть не может. Но оказывается это не так и лист Мебиуса вовсе не является простейшей односторонней поверхностью. Существует односторонняя поверхность по своей форме и процедуре своего изготовления более простая, чем классический лист Мебиуса.


Для получения действительно простейшей (элементарной) односторонней поверхности необходимо взять полоску (см. Рис. 3) и соединить между собой часть ее краев таким образом, чтобы зеленые стрелки "А" и "Б" совпали между собой, как по направлению, так и по своей длине. В результате будет получена односторонняя поверхность, показанная на Рис. 4. Очевидно, что для этого вовсе не требуется поворачивать (закручивать винтом) края полоски, приведенной на Рис. 3.
Конечно, изображенную на Рис. 4 поверхность нельзя назвать листом Мебиуса, но она все равно является односторонней и ей присущи все свойства односторонних поверхностей. В том числе и одно из самых основных, предусматривающее возможность попадания из одной точки этой поверхности в любую другую, не пересекая края. Сохранение этого свойства для односторонней поверхности, изображенной на Рис. 4 очень хорошо иллюстрирует, приведенная на Рис. 5 анимация. На анимации видно, что шарик прокатывается по всей односторонней поверхности, ни разу не пересекая ее края. Таким образом, поверхность на Рис. 4 действительно имеет всего одну единую поверхность и один край.



Элементарная односторонняя поверхность может быть представлена в двух видах. В первом случае (Рис. 4) края соединенных между собой частей полоски не охватываются полоской, а во втором (Рис. 6) края соединенных между собой частей полоски охватываются полоской. Элементарная односторонняя поверхность, приведенная на Рис. 6, получается из поверхности, приведенной на Рис. 4. Для чего ее нужно просто вывернуть как бы наизнанку. По своим свойствам поверхности представленные на Рис. 4 и 6 полностью одинаковы.

Описывается элементарная односторонняя поверхность в цилиндрических координатах следующими уравнениями:
X = R • Cos(A)
Y = R • Sin(A)
Z = H + (2•π - A) • 200 / 2•π , где
A = 2•π - (F - 2•π • [F / 2•π ]) • (1 - [H / (B+1)]);
R = L + [A / 2•π] • F;
B – ширина полосы, из которой была изготовлена односторонняя поверхность; L – радиус изгиба полоски; F – параметр, представляющий собой полярный угол, изменяемый от 0 до N•π (чем больше N, тем длиннее соединение краев полосы); H – параметр, изменяемый от 0 до 2•B; [ ] – знак, обозначающий целую часть числа и предусматривающий отбрасывание дробной части от результата вычисления выражения, стоящего в скобках [ ].
При помощи выше приведенных уравнений можно построить как элементарную одностороннюю поверхность показанную на Рис. 4, так и поверхность показанную на Рис. 6. Для построения элементарной односторонней поверхности показанной на Рис. 6 надо только в выражении для вычисления R знак "+" поменять на знак "-".
Посмотреть как происходит поточечное построение элементарных односторонних поверхностей при помощи выше приведенной системы уравнений можно запустив выполнение специальной программы: http://stob2.narod.ru/nemebiys/postroenie.exe.
Если сравнить приведенную здесь систему уравнений для описания элементарной односторонней поверхности с системой уравнений для описания традиционного листа Мебиуса (http://stob2.narod.ru/13s.htm), то сразу станет понятно, что последняя система уравнений выглядит значительно более сложной.
Из-за того, что традиционный лист Мебиуса представляет собой закрученную винтом поверхность соединять его края между собой весьма затруднительно. А вот у элементарной односторонней поверхности в этом проблем не возникает, мы легко можем соединить ее края между собой. В результате будет получена также односторонняя поверхность по своей форме напоминающая сумку. Сплетенная из нитей такая "сумка" показана на Рис. 7.
На Рис. 7 края элементарной односторонней поверхности соединены частично лишь для того, чтобы легче было понять форму поверхности. В элементарной односторонней поверхности в отличие от традиционного листа Мебиуса края можно соединить полностью. В этом случае будет получена "сумка" с двумя противоположно направленными входными отверстиями. Поверхность "сумка" также является односторонней. В чем можно убедиться, просмотрев анимацию движения шарика по ее поверхности на Рис. 8.

На анимации (Рис. 8) видно, что шарик прокатывается по поверхности "сумка" периодически проходя как по внешней, так и по внутренней ее части, но при этом ни разу не пересекая ее края. Таким образом, поверхность на Рис. 7 действительно имеет всего одну единую поверхность, и ее внутренняя поверхность фактически является продолжением наружной поверхности.
Еще одним подтверждением того, что элементарная односторонняя поверхность имеет более простую геометрическую форму чем классический лист Мебиуса является реальная возможность строить дома, здания и различные сооружения с односторонней поверхностью в виде элементарной односторонней поверхности (Рис. 4). Выглядеть подобное сооружение может примерно так, как показано на Рис. 9. На Рис. 9 применена наиболее сложная для возведения вертикальная ориентация сооружения, но все сооружение можно положить и набок и тогда все свойства односторонней поверхности будут сохранены, а построить его станет еще проще.

июнь 2010 года