| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
Лента (лист) Мебиуса, пожалуй, является одной из самых популярных геометрических фигур. Главная ее особенность состоит в том, что она имеет только одну поверхность.
Изготовить ленту очень просто. Надо взять полоску бумаги, повернуть один конец на 180 градусов и затем склеить оба конца. Более строго в топологии лист Мебиуса описывается, как неориентируемая поверхность с нулевой эйлеровой характеристикой, ограниченная одной замкнутой линией. Уравнений, однозначно задающих лист Мебиуса, не существует.
Исходя, из словесного описания листа Мебиуса, можно утверждать, что для однозначного его задания математической формулой достаточно составить уравнение пространственной замкнутой линии, ограничивающей лист.
После получения уравнения, задающего произвольную пространственную линию (см. статью "Задание пространственной линии одним уравнением") стало возможным составление уравнения пространственной замкнутой линии, ограничивающей лист Мебиуса. Конечно, здесь речь не идет о получении универсального уравнения, например такого, как для задания окружности, т. к. лента Мебиуса может быть весьма разнообразна по своей форме, например, она может быть закручена на несколько оборотов или полоса, ее образующая, сильно отличаться по форме от прямоугольника. В связи с этим каждый лист Мебиуса будет определяться своим уравнением.
Ниже приведен пример уравнения определяющего лист Мебиуса, ограниченного пространственной замкнутой линией, составленной из четырех дуг окружностей и закрученный один раз на 180 градусов.
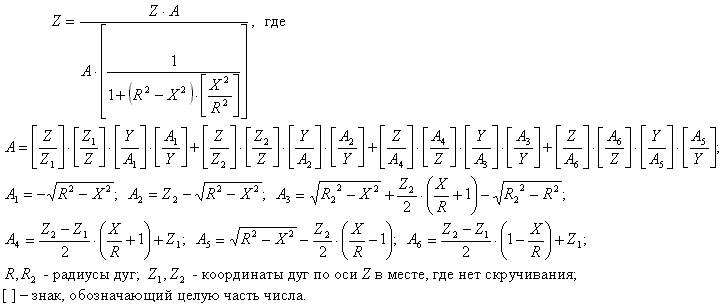
Ниже на рисунке приведен график этого уравнения, построенный при R=100; R2=110; Z1=1:Z2=21. На графике дуги, составляющие, ограничивающую лист Мебиуса, пространственную замкнутую линию выделены различными цветами.

В целях обеспечения более лучшего понимания устройства, заданного, приведенным выше уравнением, листа Мебиуса ниже приведена анимация вращения листа Мебиуса.

сентябрь 2005 года