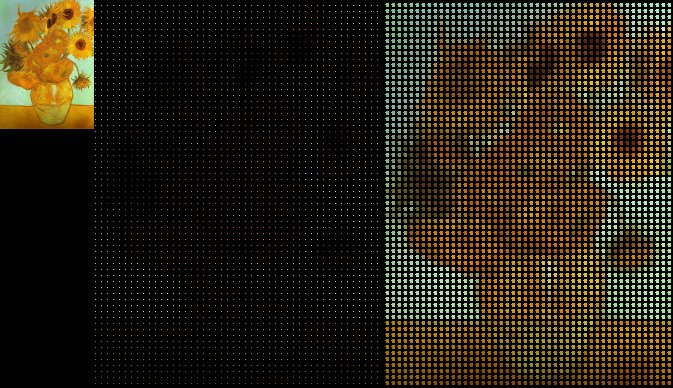
Рис. 1 Примеры простых поверхностей, на которые нанесено изображение картины ''Двенадцать подсолнечников в вазе'' Ван Гога Винсента
| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
Обычно поверхность определяется как множество точек, координаты которых удовлетворяют некоему определённого вида уравнению. Однако считается, что математически строгое определение поверхности все же основывается на понятиях топологии. При этом основным является понятие простой поверхности, которая представляет собой образ гомеоморфного отображения внутренности квадрата, т. е. взаимно однозначного и взаимно непрерывного отображения. А в более общем виде поверхность вообще рассматривается просто, как двумерное многообразие в пространстве.
Подразумевается, что такие определения поверхности исчерпывающи и полны, но так ли это? Ведь, если посмотреть на, то, что лежит в основе используемых в этих определениях терминов, то можно без труда обнаружить геометрическую точку.
Тут необходимо пояснить, что определить понятия гомеоморфного отображения или многообразия без использования понятия точки весьма затруднительно, а уж применять эти понятия вообще невозможно.
При этом известно, что точка, являясь одним из основных понятий геометрии и используемая при определении практически всех остальных понятий, так до наших дней и не имеет четкого определения. А это означает, что определить или описать точку практически невозможно. В геометрии, топологии и в других близких разделах математики точкой называют абстрактный объект в пространстве, не имеющий ни объема, ни площади, ни длины, ни каких-либо других измеримых характеристик. Таким образом, в лучшем случае точку можно представить, как некий бесконечно малый лишь потенциально существующий объект. Но этого недостаточно для однозначного использования понятия точки при определении других геометрических объектов. И в результате при определении различных геометрических объектов, совершения с ними тех или иных манипуляций, изучения их свойств, приходится использовать, так называемые, многочисленные общепринятые правила, ограничения или допущения. И, конечно же, используемые допущения, правила и ограничения, именно приняты без каких либо объективных доказательств. А это в свою очередь приводит к многочисленным, явно не относящимся к лженаучным, парадоксам, неразрешимым проблемам, вопросам, которые обычно предпочитают не только не обсуждать, но даже и не упоминать. То есть в этих случаях просто вступает в действие так называемый "научный фильтр", который блокирует всякое опубликование в специализированных изданиях и обсуждение, во всяком случае, публичное, в профессиональной среде всякой информации противоречащей или хотя бы не подкрепляющей общепринятые в науке представления.
Такие "научные фильтры" действуют и уже давно во всех науках и, конечно, в том числе и в математике. Но если, например, в физике или исторической науке явление можно объявить противоречащим законам, усомниться в чистоте проведенного эксперимента, сделанного наблюдения, а в отношении откопанного артефакта, как минимум, всегда можно заявить об ошибочности его датировки и по этим основаниям объявить их лженаучными, то в математике такой возможности, как правило, нет. И такое положение дел характерно для математики в первую очередь потому, что именно в ней используется наибольшее количество допущений, понятий, которые были не установлены экспериментальным путем, а приняты, просто как наиболее разумные на момент их принятия.
С одной стороны использование "научного фильтра" несомненно, является очень даже полезным, так как обеспечивает стабильность. Ведь в математике можно чуть ли не до бесконечности, а главное очень часто, задавать вопросы, не требующие экспериментального подтверждения и одновременно не укладывающиеся в принятые представления или ставящие их под сомнение. Но, в силу действия "научного фильтра", эти вопросы просто замалчиваются, и вся сложившаяся система представлений и понятий не сотрясается каждый раз и по любому поводу.
Однако с другой стороны, когда при помощи математики начинают что-то описывать, прогнозировать, т. е. делать именно то, ради чего, собственно, и была создана математика, насколько можно быть уверенным в ее адекватности? Не получается ли в результате нечто внешне не противоречивое, но представляющее собой лишь один из возможных вариантов? И насколько полученный вариант соответствует действительности?
Конкретные примеры, имеющихся ввиду в данной статье, вопросов и проблем начнем рассматривать с наиболее простых. Хотя простыми они являются лишь по форме, а не фактически. На Рис. 1 слева показана простая поверхность (если исходить из определений топологии), на которую для удобства отслеживания ее деформаций нанесено изображение картины "Двенадцать подсолнечников в вазе" Ван Гога Винсента.
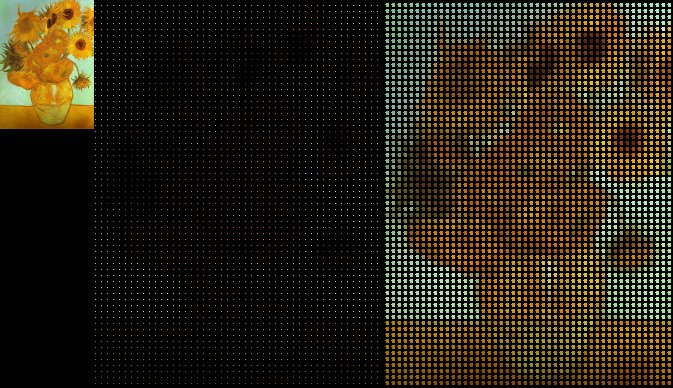
Если представленную слева на Рис. 1 простую поверхность рассматривать, как некое множество точек, то при ее равномерном растяжении будет получено нечто изображенное в центре на Рис. 1. Почему нечто? Потому что при растяжении между точками, составляющими поверхность, появятся разрывы и поверхность перестанет быть сплошной. Она просто распадется на отдельные точки. Но в топологии такое растяжение поверхности просто не предусмотрено. (Не невозможно, а именно не предусмотрено) Поверхность должна оставаться непрерывной. Тогда как же происходит растяжение, если рассматривать его на уровне отдельных точек?
Поверхность может оставаться сплошной при двух вариантах процесса (модели) растяжения. Первый и самый очевидный из этих вариантов, это когда по мере растяжения растягиваются и сами точки примерно так, как это показано на правом изображении Рис. 1. Как видно, в определенных пределах даже изображение картины становится узнаваемым.
Однако при этом варианте возникают следующие вопросы ответы, на которые не существуют. На сколько можно растянуть точку, прежде чем ее уже нельзя будет рассматривать в качестве точки? Могут ли точки в целях сохранения целостности и недопущения появления разрывов в поверхности иметь различную форму или пересекаться? Могут ли точки содержать в себе другие точки или отдельные их части? Что будет происходить с точками, составляющими поверхность при ее неограниченном растяжении? Что будет происходить с точками, составляющими поверхность при ее неограниченном сжатии? Или существует ли предел степени сжатия поверхности, после которого сжимаемая поверхность уже перестанет быть поверхностью?
Ответы на эти вопросы не существуют, поскольку не существует четкого определения точки. Для точки не определены ни ее размеры, ни ее форма, ни степень однородности (одинаковости) двух разных произвольных точек. Без предварительного определения этих параметров точки говорить о рассматриваемом механизме (модели) деформирования поверхности вообще бессмысленно, равно, как и пытаться дать ответы на приведенные выше вопросы.
Второй вариант процесса (модели) растяжения может заключаться в том, что по мере растяжения поверхности к ее краю добавляются новые точки, берущиеся как бы из ниоткуда и в неограниченном количестве. При сжатии лишние точки соответственно убираются в никуда. При этом варианте деформирования казалось бы все проблемы и противоречия должны бы быть устранены, но так может показаться лишь на первый взгляд и если не задумываться о деталях процесса деформирования поверхности. Но если глаза не закрывать, то все неудобные вопросы для рассмотренного выше первого варианта практически остаются.
Так изначально сплошная поверхность при деформировании должна оставаться сплошной (если, конечно, разрывы в ней не создаются умышленно). Но для обеспечения этого придется вернуться к вопросу: Могут ли точки в целях сохранения целостности и недопущения появления разрывов в поверхности иметь различную форму или пересекаться? Так как точки, например, шарообразные по своей форме никак не могут плотно контактировать друг с другом. Между ними обязательно будут появляться пустоты. Если, конечно, исключать случаи их взаимных пересечений.
В топологии считается очень важным обеспечение непрерывности. Но тогда возникает вопрос, как же можно обеспечить непрерывность растяжения поверхности при добавлении к ней точек, которые фактически являются дискретными объектами? Кстати допущение взаимных пересечений точек в этом случае дискретность не устранит.
Если все же допустить дискретность (ступенчатость) процесса любого деформирования поверхности, то, как определиться с местонахождением конкретной добавляемой точки (или если говорить иначе, то с шагом деформирования)? Просто заявить, что это не является важным - не получится, так как практически становится невозможным выполнение важнейшей операции – выделение так называемых концевых или краевых точек. Останется только утверждать, что такие точки должны существовать и существуют, но лишь потенциально. А ведь подобная проблема существует не только с концевыми или краевыми точками, но вообще с любой точкой поверхности. Вот и получается, что когда говорят о конкретной точке и ее окрестности, а делать это приходится очень часто, то практически никто понятия не имеет о какой конкретно точке и окрестности, собственно говоря, идет речь. Конечно, можно попытаться заявить, что точка размеров не имеет и представляет собой что-то вроде координат, но тогда она исчезает, как объект и не может добавляться к деформируемой поверхности, а понятие координат в топологии вообще не применяются, поскольку в ней не рассматриваются метрические свойства объектов. Сами же координаты это просто величины, определяющие положение точки или тела в пространстве и, исходя из одного этого, уже никак не могут заменить собой понятие точки.
В этой связи является очевидным, что остаются без ответов так же и следующие вопросы: Что будет происходить с точками, составляющими поверхность при ее неограниченном сжатии? Или существует ли предел степени сжатия поверхности, после которого сжимаемая поверхность уже перестанет быть поверхностью?
Таким образом, адекватной и непротиворечивой модели процесса деформирования поверхности не существует. Никто не имеет никакого представления, как происходит процесс деформирования на уровне отдельных точек составляющих поверхность и что собой представляет контакт между точками. Предложения по исправлению этой ситуации тоже не поступают и поэтому математики деформируют поверхности, не распространяясь по поводу деталей этого процесса. А если какая то часть рассматриваемого объекта все же неизбежно вырождается в одну единственную точку, то такие объекты тут же исключаются из существующих классификаций геометрических объектов так или иначе объявляются неправильными, вообще не поймешь чем, и исключаются из рассмотрения.
По этому принципу, например, из состава многообразий исключается отрезок (имеет две концевые точки) или коническая поверхность (имеет вершину в виде одной точки, в которой сходятся две ее полости). О других примерах подобных действий и парадоксах, к которым они приводят можно прочитать в статье: " Многогранник – единая и универсальная геометрическая форма всего" ( http://stob2.narod.ru/10i.htm).
Такая позиция похожа на позицию страуса засунувшего голову в песок. Ведь сколько голову в песке не держи, не закрывай глаза, неудобные вопросы и парадоксы сами собой не исчезнут.
На Рис. 2 показан шар с отображенной на его поверхность картиной "Leda Atomica" Сальвадора Дали и тор с отображенной на его поверхность картиной "Мона Лиза", она же "Джоконда" Леонардо да Винчи.

Нанесение изображения картин на поверхности шара и тора указывает, что эти геометрические объекты были получены или, во всяком случае, могли быть получены путем деформирования изначально прямоугольных поверхностей картин.
В топологии утверждается, что деформировать кусок плоскости в поверхность шара или тора без выполнения, так называемых, склеек невозможно. То есть и шар и тор на Рис. 2 должны иметь склейки. Действительно любой желающий на показанных, на Рис. 2 геометрических объектах без труда сможет указать на склейки, которые присутствуют на поверхности шара и тора. Но, что будет, если этот шар или тор получить из куска плоскости на поверхность, которой будут нанесены ни достаточно контрастные изображения картин, а однородный и неконтрастный рисунок. А будут получены шар и тор (см. Рис. 3) практически точно такие же, как и показанные на Рис. 2.

Вот только показать на них склейки уже никто не сможет и это несмотря на то, что и шар и тор на Рис. 3 пусть и виртуально, но действительно были получены из прямоугольного куска плоскости.
Получается парадокс, топологи утверждают, что в только что описанном случае поверхность шара или тора в обязательном порядке должны содержать склейки, но практически найти их никто не может и назвать признаки, по которым их можно найти на указанных поверхностях тоже не могут.
Так может в данном случае наличие склеек вовсе не так уж и обязательно? Или, во всяком случае, необязательно наличие склеек в том виде в каком обычно их представляют топологи?
Однако тогда должны существовать иные способы деформации куска плоскости в поверхность шара или тора, нежели те, что обычно описываются топологами. И они есть. Так, например, на Рис. 4 показан процесс постепенного растяжения небольшого куска плоскости до поверхности шара, а на Рис. 5 – процесс постепенного растяжения небольшого куска плоскости до поверхности тора.


На представленных, на Рис. 4 и 5 анимациях моменты возникновения склеек вроде бы видны, но вот только такие склейки очень не похожи на традиционные представления о склейках, так как они представляют собой одиночные точки. И тогда возникает вопрос – может ли точка являться склейкой, а склейка, соответственно точкой?
Если на этот вопрос ответить "нет", то тогда придется признать, что кусок плоскости можно деформировать в поверхность шара без выполнения склеек. Если же на этот вопрос ответить "да", то склейку придется рассматривать в качестве лишь потенциально существующего с совершенно неопределенными свойствами объекта. Об этом объекте естественно будет известно никак не больше, чем о геометрической точке и соответственно практически показать его будет невозможно. А тогда с равной долей успеха можно будет подтверждать или отрицать сам факт существования такой склейки.
Таким образом, любой ответ на этот вопрос вряд ли может устроить. Впрочем, в настоящее время эта проблема решается традиционным путем – о ней просто не упоминают. Именно так поступают, когда в каком либо объекте происходит выделение отдельной точки и его невозможно объявить несуществующим или хотя бы исключить из существующих классификаций геометрических объектов.
Впрочем, если бы проблема была только лишь в невозможности практически выделить на поверхности склейку, то к существующим в математике представлениям вопросов было бы не так уж и много и они не были бы по настоящему важными. Ведь склейку, например, всегда можно объявить не частью конкретной поверхности, а лишь операцией, которая выполняется при ее формировании (если хотите, изготовлении).
По настоящему серьезная проблема заключается в том, что оказывается отображение плоскости на поверхность, например, шара можно осуществить разными способами. И от того, каким способом будет происходить отображение, будет зависеть признание его в качестве непрерывного, то есть такого отображения, у которого малые изменения аргумента приводят к малым изменениям значения отображения, или иначе, у которого близкие точки переходят в близкие.
Действительно, если в представленной на Рис. 4 анимации, первую точку, с которой начинается формирование поверхности шара взять из центральной части некой плоскости, а затем все последующие точки поверхности шара брать из той же плоскости постепенно двигаясь по спирали вокруг центральной самой первой точки и также двигаясь по спирали переносить их на поверхность шара, как это показано на Рис.4, то все близкие точки поверхности плоскости будут переходить в близкие точки поверхности шара или, говоря иначе, произойдет непрерывное отображение поверхности плоскости на поверхность шара.
Казалось бы, подумаешь важная проблема - при одном способе отображения плоскость отображается на поверхность шара непрерывно, а при другом нет? Однако эта ситуация ставит под сомнение одно из основных понятий топологии – понятие гомеоморфизма.
Гомеоморфизм в топологии - это взаимно-однозначное и непрерывное отображение, обратное к которому тоже непрерывно.
Поверхности, связанные гомеоморфизмом, считаются топологически неразличимыми.
А в только, что описанном выше случае возникает парадокс – при одном способе отображения поверхность шара и плоскости топологически неразличимы, а при другом очень даже различимы. То есть существующее определение гомеоморфизма становится несостоятельным, а за ним последуют и остальные понятия топологии.
Следует отметить, что этот парадокс стал возможен тоже только благодаря тому, что при отображении мы имеем дело с точками, которые из-за неопределенности их вида можно смещать друг относительно друга, как угодно и заявлять о каком угодно их количестве на единице площади поверхности.
Таким образом, принятая в топологии модель отражения окружающего мира вызывает сомнения в своей достаточной адекватности, в том числе и для целей практического применения.
Но, несмотря на существующие проблемы, парадоксы и вопросы без ответов, чисто теоретические результаты исследований в топологии продолжают распространять на окружающий мир и утверждать о том, что при помощи топологии в ее настоящем виде окружающий мир описывается достаточно адекватно.
Из последних наиболее известным подобным утверждением, конечно же, является доказательство знаменитой гипотезы Пуанкаре: "Всякое односвязное компактное трехмерное многообразие гомеоморфно трехмерной сфере". Утверждается, что доказательство именно этой гипотезы помогает определиться с формой нашей вселенной.
Правда никто не говорит о том, что это доказательство действительно будет чему-то помогать только в том случае, если существующая на сегодняшний день топология действительно в достаточной степени адекватна окружающему миру. То есть, если удастся сформулировать вопросы, найти противоречия, проблемы способные поставить хотя бы под сомнение гипотезу Пуанкаре, то это однозначно будет означать, что современная топология недостаточно адекватна и говорить о том, что она чему-то помогает вообще то преждевременно.
Как обнаружить такие противоречия и проблемы, в общем-то, известно – надо просто все или частично (обычно бывает достаточно) детализировать до отдельных точек. Рассмотрим эту возможность на примере двумерного варианта гипотезы Пуанкаре: "Всякое односвязное компактное двумерное многообразие гомеоморфно двумерной сфере".
Двумерный вариант выбран просто потому, что он проще, является более понятным и не требует обращаться к четырехмерному пространству.
На Рис. 6 представлена схема формирования односвязного компактного многообразия негомеоморфного двумерной сфере.

Формирование осуществляется следующим образом. Берутся две одинаковые сферы, показанные в верхних левом и правом углах на Рис. 6. Затем их деформируют путем вдавливания части поверхности сфер вовнутрь. При этом получают вогнутые полусферы (на Рис. 6 показаны зеленым цветом) и плоские торцевые поверхности (на Рис. 6 показаны красным цветом). После объединения двух полусфер по красным торцевым поверхностям получают поверхность сферической оболочки, которая состоит из внешней части синего цвета и внутренней части зеленого цвета.
Так вот полученная поверхность сферической оболочки никак не может быть гомеоморфна двумерной сфере, но при этом она односвязна и компактна.
Конечно, можно заявить, что поверхность сферической оболочки, не содержащая отверстий, не является многообразием. Однако существующие определения многообразия и поверхности вообще-то не содержат запретов на существование многообразий состоящих из двух и более частей непосредственно друг с другом не контактирующих. Возможно, забыли прописать? Возможно, посчитали это обстоятельство само собой разумеющимся? Хотя раз существуют такие геометрические объекты, то рассмотрение их внутренней и наружной поверхности в качестве двух разных поверхностей вовсе не является очевидным.
Но даже, если рассуждать так, то ведь существует вариант, когда точки синей и зеленой частей поверхности оболочки будут соприкасаться друг с другом по всей площади полусфер. А площадь красных торцевых поверхностей будет равна нулю. Тогда синяя и зеленая часть поверхности оболочки объединятся в одну единственную часть. Да и вариантов их склейки между собой существует несколько. Вот только представить себе или описать такой контакт невозможно, так как для этого потребовалось бы описать параметры точки. А это уже означает, что ни подтвердить, ни опровергнуть возможность существования подобного многообразия не представляется возможным. Таким образом, имеем проблему, ставящую под сомнение гипотезу Пуанкаре.
сентябрь 2011 года