
Рис. 1 Куб
| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
В первой части статьи Неудобные вопросы и парадоксы современной топологии http://stob2.narod.ru/33s.htm было показано, что все основные пока нерешенные вопросы в топологии так или иначе связаны с отсутствием четкого определения понятия геометрической точки. Рассматривались проблемы, связанные с неопределенностью размеров, формы точки, количества точек и взаимодействия точек между собой.
В этой части статьи рассмотрим проблемы, возникающие в связи со следующим вопросом: Одинаковы ли по своим свойствам геометрические точки, составляющие объекты различной размерности? То есть, например, отличаются или нет точки двумерного объекта от точек трехмерного объекта (например, квадрата и куба)?
Существующее в настоящее время определение точки - абстрактный объект в пространстве, не имеющий ни объема, ни площади, ни длины, ни каких-либо других измеримых характеристик. С одной стороны прямо на этот вопрос ответа не дает, но с другой стороны его можно истолковать и как, то, что точка всегда одинакова во всех пространствах и для всех объектов, если, конечно, не обращать внимание на то, что в определении точки не уточняется о каком пространстве идет речь, двумерном, трехмерном, четырехмерном и т. д.? Или имеется ввиду точка, соответствующая только пространству определенной размерности?
Конечно, можно сказать, что, затрагиваемый здесь вопрос несущественен, и не оказывает никакого влияния. И никакой проблемы здесь просто нет. Вот поэтому и не уточняется. Однако существуют серьезные основания подозревать, что эта проблема, точно так же, как и многие другие, замалчивается умышленно.
Поясним, возникающую проблему, на конкретном примере. На рис. 1 представлен куб, который вначале будем рассматривать, как замкнутую поверхность или, если говорить на языке топологов, как двумерное многообразие.

Теперь деформируем этот куб путем сжатия. Причем, как уже отмечалось в первой части статьи, для того чтобы выявить все, возникающие при этом проблемы, деформировать мы его будем до проявления отдельных точек, составляющих этот куб. Процесс деформирования куба, представленного на Рис. 1 очень наглядно показан на Рис. 2 при помощи анимации.

Для более удобного наблюдения процесса деформации у куба была удалена передняя грань.
Как видно на Рис. 2 сначала ничего необычного не происходит. Боковые грани куба просто равномерно сжимаются, но потом, когда высота боковых граней практически стала равна нулю, верхняя и нижняя грани куба на ложились друг на друга, и полностью совпали. Все точки, составлявшие куб расположились в один слой, а куб деформировался в кусок плоскости в виде квадрата. При этом, так как верхняя грань куба на ложилась на нижнюю грань куба по всей своей поверхности, а не состыковались между собой в стык, то нельзя сказать, что была осуществлена их склейка. С точки зрения тополога не только склейка будет неправильной, не соответствующей общепризнанным правилам, но и все подобное деформирование будет не соответствовать общепринятым представлениям о выполнении деформирования (отображения), а значит, уже в силу этого, в рамках современной топологии не подлежит рассмотрению.
Затем получившийся квадрат в свою очередь сжали до отрезка, а отрезок вообще сжали до точки.
Кроме этого, если можно было выполнить сжатие, то значит, выполнив все операции в обратном порядке можно деформировать точку, отрезок и квадрат в куб. Во всяком случае, препятствий для практического выполнения этой процедуры не существует. А это уже может позволить заявить о гомоморфизме всех этих объектов.
Но и это еще не все. Представьте себе, что куб на Рис. 1 полнотелый, то есть он не является поверхностью, а представляет собой обычное трехмерное многообразие. Ведь тогда в ходе его деформирования вообще не возникнет ничего даже отдаленно напоминающее склейку.
Тогда из каких соображений подобные деформации не стремятся рассматривать в рамках современной топологии? Для получения представления о мотивах побуждающих практически не замечать подобные превращения с геометрическими объектами возьмем сферу, обтянутую холстом (Рис. 3) и картину Макса Эрнста «Ангел очага или триумф сюрреализма» (Рис. 4), с геометрической точки зрения представляющую собой просто прямоугольный кусок плоскости.


И отобразим картину (Рис. 4) на сферическую поверхность холста (Рис. 3).
С позиций топологии и холст и картина представляют собой топологические пространства, заданные равными множествами, состоящими из одинаковых элементов – точек. Кроме этого будет заявлено, что, так как эти два пространства состоят из разного числа точек, то при выполнении отображения картина станет подмножеством множества, определяющего поверхность холста. Процесс такого отображения показан при помощи анимации на Рис. 5.

Если бы сфера была бы полнотелым шаром, то по представлениям топологии отобразить в нее картину было бы нельзя (но ни на ее поверхность).
Для того чтобы подобные ограничения имели право на существование необходимо выполнение двух условий:
1. Точки топологических пространств разных размерностей (для рассматриваемого примера это двумерное и трехмерное пространства) должны отличаться друг от друга и соответственно множества, определяющие такие пространства (объекты) должны состоять из разных элементов.
2. Множества, определяющие два отличных друг от друга топологических пространства должны иметь возможность состоять из разного числа элементов (для топологических пространств – разного числа точек).
Однако соблюдение этих двух условий вовсе не является очевидным. Как уже выше отмечалось из определения точки невозможно понять, существуют ли, или хотя бы могут теоретически существовать, различные по своим свойствам точки. И главное, пока не существует отличительных признаков, по которым можно бы было отдельно взятую точку, например, двумерного объекта отличить от отдельно взятой точки трехмерного объекта. Таким образом, не существует доказательств того, что точки топологических пространств разных размерностей отличаются друг от друга. А это в свою очередь позволяет утверждать, что отсутствуют, какие либо основания заявлять о том, что множества, определяющие топологические объекты различной размерности состоят из отличных друг от друга элементов.
Вообще-то множества могут быть любыми по количеству своих элементов, но способны ли конечные множества точек полностью определить хоть один геометрический объект? Конечно же, нет. И все потому, что точка не имеет измеримых характеристик, а значит в любом месте, обозначенном некоторыми координатами (x,y,z) должно находиться бесконечное число точек. Иначе все геометрические объекты и очень большие, и совсем маленькие состоят из одинакового бесконечного числа точек. На практике это означает то, что художник без проблем всегда сможет заполнить всю поверхность холста на Рис. 3 копией картины, какой бы изначально маленькой или большой она бы ни была. Отображение же картины Макса Эрнста «Ангел очага или триумф сюрреализма» на поверхность сферы, обтянутой холстом, так как показано на Рис. 5 является всего лишь одним из возможных вариантов выполнения отображения.
И потом, что делать, если будет взята картина площадью равная или большая площади холста на сфере? Заявить, что отображение невозможно? Но ведь практически отображение выполняют, и никаких лишних точек при этом не остается.
Что же вынуждает не замечать все эти парадоксы? Стремление сохранить стабильность существующих представлений, не сделать их описаниями просто частных случаев? Ведь уточнить понятие точки с тем, чтобы устранить все парадоксы в обозримом будущем вряд ли удастся. Это, как самая важная, так и самая сложная проблема математики. И ничего не остается, как, не обращая внимания на все противоречия, продолжать рассуждать об окрестности точки, и при этом понятия не имея, а что же из себя, представляет точка. Ведь это позволяет без лишних проблем использовать хорошо изученный существующий уже ни одно десятилетие математический аппарат.
Когда задается любой топологический объект, то он, по утверждению топологов, задается бесконечным множеством элементов – точек. Однако, это не совсем так. Фактически он обычно задается при помощи уравнений или системы уравнений, которые и определяют множества элементов топологических объектов.
На первый взгляд такое уточнение фактически используемого способа задания топологических объектов является несущественным, но это тоже не так.
Почему такое уточнение имеет важные последствия, рассмотрим на примере взаимных перемещений в трехмерном пространстве двух простых поверхностей, как их любят называть топологи, то есть просто двух кусков плоскости.
Задать кусок плоскости в трехмерном пространстве можно разными способами, при помощи различных уравнений. Например, таких, как в статье Параметрические уравнения четырехугольников (квадрат, прямоугольник, параллелограмм, трапеция) http://stob2.narod.ru/30s.htm . Для того, чтобы приблизиться к ситуации деформирования куба на Рис. 2 мы просто вырежем грани из многогранника.
Так как многогранники удобно задавать уравнениями в полярных координатах, то трансформируем систему уравнений, приведенную в статьеУравнение многогранников http://stob2.narod.ru/29s.htm к виду (1) и (2).
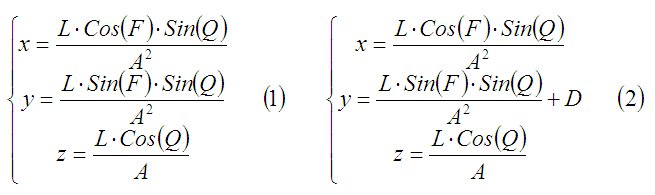
где:
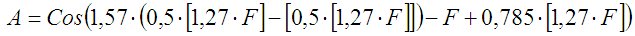
F – угол сферических координат в горизонтальной плоскости; Q – угол сферических координат в вертикальной плоскости; L – коэффициент, может быть любым числом, физически представляет собой радиус вписанной в многогранник сферы (в проекции на горизонтальную и вертикальную плоскость); D – любое число; [ ] – знак, обозначающий целую часть числа и предусматривающий отбрасывание дробной части от результата вычисления выражения, стоящего в скобках [ ]; х,у,z – координаты точек, принадлежащих поверхности многогранника.
Система уравнений (1) определяет на Рис. 6 красный прямоугольник, а система уравнений (2) определяет серый прямоугольник.

Системы уравнений (1) и (2) отличаются друг от друга прибавлением к системе уравнений (2) числа D.
Теперь наложим серый прямоугольник на красный прямоугольник аналогично тому, как это делалось при деформировании куба (Рис. 1) на анимации (Рис. 2). Получившееся в результате наложение будет определяться системой уравнений (1). На первый взгляд вроде бы никаких проблем и парадоксов не возникло, но это не так. Попробуйте серый прямоугольник вернуть на прежнее место, и у вас ничего не получится. Необходимо будет серый прямоугольник задавать вновь системой уравнений (2). Почему так происходит? Потому, что, когда говорят о задании прямоугольников множествами точек, то говорят неправду. Фактически их задают уравнениями. А это две очень большие разницы.
Сколько элементов – точек с одинаковыми координатами может содержать множество? Да, сколько угодно, хоть бесконечное число. А сколько точек с одинаковыми координатами может задать уравнение? Очевидно, что только одну.
Поэтому при наложении все точки с одинаковыми координатами объединяются в одну единственную точку, и после этого их разделить уже становится невозможно. Таким образом, широко применяемый в настоящее время математический аппарат просто не в состоянии адекватно описывать деформации, показанные на Рис. 2. Причем, как сжатия, так и расширения.
Да традиционно используемый для определения множеств точек топологических объектов математический аппарат действительно не может описывать, приведенные выше объекты. Но это ни значит, что такого математического аппарата не существует. Смотрите, например, статью Точечная графика: запись математической формулой http://stob2.narod.ru/6s.htm .
Почему же тогда стали использовать не полностью адекватно описывающий топологические объекты математический аппарат? А потому, что он удобнее и проще в применении, достаточно адекватно описывает большинство до сих пор рассматривавшихся реально существующих объектов. Все же, что не удалось адекватно описать, просто объявили не являющимся предметом изучения для топологии.
И долгое время все шло хорошо, но представления об окружающем мире постоянно уточняются и расширяются. А окружающий мир принято описывать через математические модели. Когда же известные и считавшиеся надежными математические модели вдруг перестают адекватно объяснять вновь обнаруженные явления, как раз и появляется сигнал о необходимости уточнения и дальнейшего развития математических теорий.
Сейчас таких явлений очень много накопилось, например, в космологии. Об этом можно прочитать в статье: О методах преодоления проблем Стандартной Космологической Модели строения и эволюции Вселенной, возникающих при объяснении наблюдаемых явлений после Большого взрыва http://stob2.narod.ru/13i.htm .
Однако обнаружение несоответствий вовсе не означает быстрого пересмотра математических теорий. За общепринятые представления борются до последней возможности. Даже, если речь идет не о том, чтобы их признать ошибочными, а всего лишь о том, чтобы признать, что они описывают частные случаи. Начинаются поиски неучтенных факторов. В космологии одни только поиски темных материи и энергии чего стоят.
Пересмотр представлений всегда процесс долгий и мучительный, и топология в этом плане вовсе не является исключением. Однако без этого не обойтись, если мы хотим описывать громадное количество реально существующих геометрических объектов и постоянно не заявлять, что они не являются предметом для изучения в рамках топологии. Если мы хотим понять, сколько измерений в действительности имеет окружающий нас мир, как взаимодействуют между собой двумерные, трехмерные и так далее объекты, используя соответственно третье, четвертое и так далее измерения.
март 2013 года