| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
Основное назначение математики это описание различных объектов и связанных с этими объектами процессов, явлений и т. п. Причем описания виртуальных, реально не существующих объектов, практически составляются исключительно с целью получения возможности приближенного, идеализированного описания реально существующих объектов.
Необходимо отметить, что практически все существующие в настоящее время описания (математические модели) реальных объектов являются приближенными (идеализированными). Причем весь ход развития математики и других наук показывает, что происходит постепенный переход к математическим моделям способным описывать объекты более детально.
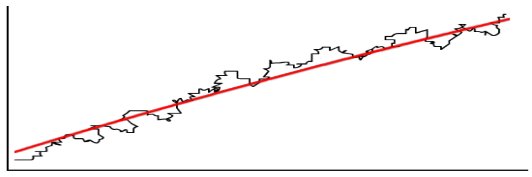
На приведенном ниже рисунке показан пример замены реального объекта (ломанная черная линия на графике) на идеализированную приближающую математическую модель (красная линия на графике).

Подобные математические модели не только часто описывают реальные объекты со значительными отклонениями, но и не могут быть заданы только в виде математической формулы (уравнения). Это связано с тем, что реальные объекты и процессы, как правило, имеют вполне конкретные пределы. Например, если рассмотреть известную из курса физики формулу для вычисления пройденного пути при равномерном прямолинейном движении s=vt, то станет очевидным, что эта формула не будет иметь смысла при скорости движения v равной отрицательным значениям или превышающим скорость света. Таким образом, чисто математически утверждение, что пройденный путь в общем случае выражается через эту формулу, является не правильным. Вообще то при записи она должна сопровождаться словесными высказываниями. Такое положение дел характерно для большинства используемых формул (уравнений).
Ситуация осложняется тем, что процесс детализации любого реального объекта по существу является бесконечным. По мере детализации приходится учитывать все более мелкие подробности и, в конце концов, любой объект перестает быть сплошным – рассыпается на отдельные составляющие его элементы, которые в свою очередь делятся на элементы их составляющие и т. д. Таким образом, реальные объекты являются дискретными и в силу этого, связанные с ними процессы, явления так же дискретны. Подавляющее же количество существующих математических моделей представлено гладкими непрерывными функциями, а для описания дискретных объектов необходимы функции, допускающие скачкообразное изменение своих значений. Такими свойствами обладают разрывные функции – функции, не являющиеся непрерывными, т. е. имеющие на рассматриваемом интервале точки разрыва. В литературе подобные функции часто называют импульсными, ступенчатыми, обобщенными, символьными, пороговыми и чаще всего их приходится задавать, используя способ задания функций словесной формулировкой или системой уравнений, объединенных условиями вида "если …, то …" или "при …".
Использование при задании функций одновременно и формул (уравнений), и словесных высказываний создает определенные неудобства, обусловленные главным образом тем, что значения таких функций невозможно определить только при помощи вычислительных операций. Кроме этого известно этих функций сравнительно немного и нельзя сказать, что они способны закрыть все имеющиеся и тем более будущие потребности. Наиболее часто встречающиеся из них вычисляемые функции это: 1/x; (x-s)0,5; (x-s)0; [x] – целая часть числа или антье от x (обозначение ввел К. Гаусс в 1808 г.). Однако приведенные функции не обеспечивают получения значений либо 0, либо 1 в зависимости от изменения x, что делает их малопригодными для описания реальных дискретных объектов. В связи с этим появились такие символьные (не вычислимые или задаваемые словесными формулировками функции), как сигнум-функция (введена Л. Кронекером в 1878 г.), символ Кронекера (введена Л. Кронекером в 1884 г.). В 20-х годах 20-го века П. Дираком в связи с проведением исследований по квантовой механике были дополнительно введены обобщенные функции (это, прежде всего дельта-функция Дирака и функция Хевисайда), которые, однако сохранили недостатки функций, введенных Л. Кронекером. Нельзя утверждать, что сложившееся положение дел всех устраивало. Импульсные и ступенчатые функции пытались и пытаются аппроксимировать непрерывными функциями. Достаточно сказать, что этому вопросу было уделено сравнительно большое внимание в очень популярном в свое время Справочнике по математике (для научных работников и инженеров) Г. Корн, Т. Корн, "Наука", М, 1974 г. К сожалению удовлетворительных аппроксимаций получить не удалось. Необходимо отметить, что, скорее всего, аппроксимацию непрерывной функцией разрывной функции вообще получить невозможно, что было показано в статье "Периодические импульсные функции на основе универсального уравнения" http://stob2.narod.ru/16s.htm на примере аппроксимации периодической импульсной функции тригонометрическим полиномом. Таким образом, особенно при описании дискретных объектов все чаще наблюдается вынужденный отказ от использования основополагающих понятий классической математики – предела и непрерывности.
Кроме этого для описания различных объектов с повышенной детальностью пытаются использовать различные матрицы. Однако использование матриц осложняется регулярностью их структуры (реальные объекты, как правило, регулярностью не отличаются) и зависимостью, получаемого описания, не только от свойств, описываемого объекта, но и от свойств выбранной матрицы, что было показано на примере в статье "Распознавание образов: математический аппарат" http://stob2.narod.ru/8s.htm.
Между тем ситуация продолжает усугубляться, так как потребности в детальных описаниях реальных объектов постоянно возрастают. В ближайшее время можно ожидать нового дальнейшего существенного обострения ситуации в связи с быстрым развитием нанотехнологий, которые обязательно потребуют очень детальных описаний на уровне наноразмеров. Попытки использования традиционных математических методов классической математики приводят к появлению очень сложных и объемных доказательств полученных утверждений, а также использованию очень объемных компьютерных расчетов, что ведет к невозможности получения достоверной оценки надежности полученных результатов. Это объективно связано с тем, что математики уже физически не в состоянии проверить доказательства объемом в несколько сот страниц, а вычислительная техника, к сожалению, работает с ошибками.
Так, например известна созданная Уоллесом теория с доказательством Великой теоремы Ферма сравнительно небольшого объема (около 150 страниц), которая была проверена и была признана надежной. Однако, приведенное Уоллесом доказательство не выявило наличие решений Великой теоремы ферма среди бесконечных целых чисел. (Существование таких решений было доказано в http://stob2.narod.ru/14s.htm. ) Таким образом, либо в выкладках Уоллеса все же есть ошибки, либо его доказательство не является общим. При этом можно отметить, что ряд целых чисел является дискретным и соответственно целые числа являются объектами дискретной математики.
В отношении того, что компьютеры делают ошибки. Например, если вычислить при помощи встроенного в windows калькулятора или программы Microsoft Visual Basic выражение 00, то компьютер выдаст, что 00=1, хотя должен выдать сообщение об ошибке.
Из выше сказанного следует, что попытки применить для описания дискретных объектов методы классической математики или символьные функции, скорее всего, являются тупиковыми. Поэтому в целях преодоления отмеченных трудностей можно предложить использовать следующие функции, полученные на основе вычислимых разрывных функций.
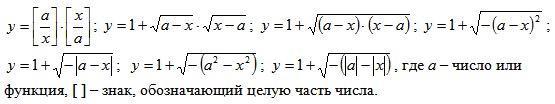
Необходимо отметить, что с одной стороны подобных функций можно составить очень много, а с другой стороны свойством принимать значения равные нулю или единице обладает только первая, из приведенных, функция и возможно по этим своим свойствам она является уникальной. Остальные функции могут только принимать значения равные единице или не иметь значений, что сильно ограничивает область их применения.
Конечно и используя в основном одну эту, по-своему уникальную функцию, для составления на ее базе новых функций можно получить описания самых различных и очень сложных объектов. Однако имеются и очень существенные недостатки. Это, прежде всего быстрый рост объема описания по мере усложнения описываемого объекта и недостаточная предсказательность получаемых математических моделей, т. е. объект очень хорошо описывается лишь, как он есть.
декабрь 2006 года