| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
После получения уравнения способного задавать (описывать) в полярных координатах практически любой правильный многоугольник (см. статью: "Уравнение правильных многоугольников в полярных координатах" http://stob2narod.ru/27s.htm) появилась возможность, используя это уравнение описывать многогранники и им подобные тела в цилиндрических и сферических координатах. Это связано, прежде всего, с тем, что многогранник представляет собой геометрическое тело, имеющее поверхность, состоящую из многоугольников.
Цилиндрические координаты определяются радиусом R и углом F и связаны с прямоугольными координатами X, Y и Z формулами: X=R*CosF, Y=R*SinF, Z=Z. Подставив в эти формулы вместо радиуса R выражение описывающее в полярных координатах многоугольник получим систему уравнений (1) описывающую боковую поверхность различных многогранников. В данном случае призм.
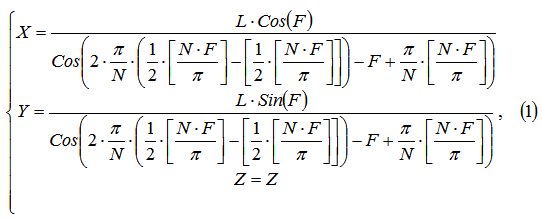
где F – угол; L – коэффициент, может быть любым числом, физически представляет собой радиус вписанного в многогранник цилиндра; N – коэффициент, может быть любым числом, от его значения зависит вид, количество сторон (углов) многогранника; π - число пи, равное 3,14159…; [ ] – знак, обозначающий целую часть числа и предусматривающий отбрасывание дробной части от результата вычисления выражения, стоящего в скобках [ ].
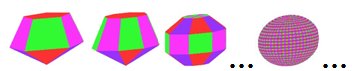
Ниже приведены примеры боковых поверхностей многогранников построенных при помощи системы уравнений (1) на основе правильных самонепересекающихся многоугольников, т. е. для целых значений N из ряда 3, 4, 5, …..:

У таких поверхностей количество боковых граней равно значению коэффициента N и при стремлении N к бесконечности поверхность, задаваемая системой уравнений (1) стремится к гладкой цилиндрической поверхности.
Окраска на рисунках в данной статье никак не связана с рассматриваемыми уравнениями и выполнена для обеспечения лучшего восприятия, приводимых в качестве примеров геометрических тел.
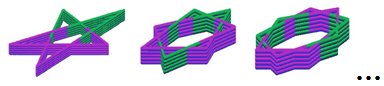
Для всех N представленных числами с дробной частью система уравнений (1) будет определять ряд самопересекающихся поверхностей, примеры, которых приведены ниже:
В статье: "Уравнение спиралей в виде многоугольников в полярных координатах" (http://stob2.narod.ru/28s.htm) было показано, как можно преобразовать уравнение правильных многоугольников в полярных координатах в уравнение спиралей. Действуя по аналогии можно получить из системы уравнений (1) систему уравнений, задающую различные спиральные поверхности примеры, которых приведены ниже на рисунке:

Сферические координаты определяются радиусом R и углами F и Q и связаны с прямоугольными координатами X, Y и Z формулами: X=R*CosF*SinQ, Y=R*SinF*SinQ, Z=R*CosQ. Подставив в эти формулы вместо радиуса R выражения, описывающие в полярных координатах многоугольники можно получить систему уравнений (2) описывающую различные многогранники.
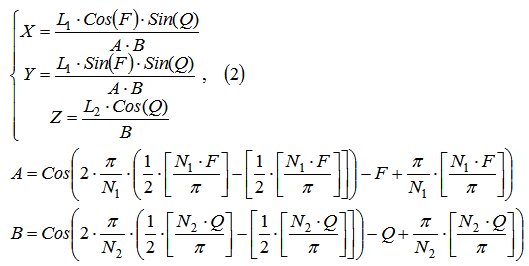
где F – угол сферических координат в горизонтальной плоскости; Q – угол сферических координат в вертикальной плоскости; L1 – коэффициент, может быть любым числом, физически представляет собой радиус вписанной в многогранник сферы (эллипсоида в проекции на горизонтальную плоскость); L2 – коэффициент, может быть любым числом, физически представляет собой радиус вписанной в многогранник сферы (эллипсоида в проекции на вертикальную плоскость); N1 – коэффициент, может быть любым числом, от его значения зависит вид, количество сторон (углов) многогранника в проекции на горизонтальную плоскость; N2 – коэффициент, может быть любым числом, от его значения зависит вид, количество сторон (углов) многогранника в проекции на вертикальную плоскость; π - число пи, равное 3,14159…; [ ] – знак, обозначающий целую часть числа и предусматривающий отбрасывание дробной части от результата вычисления выражения, стоящего в скобках [ ].
Необходимо отметить, что система уравнений (2) несколько отличается от традиционной системы уравнений для сферических координат. Прежде всего, тем, что сферический радиус R принимает при вычислении координат X, Y и Z разные значения, так как выражения в системе уравнений (2) L1/(A*B) и L2/B не равны друг другу.
При целых значениях N1 из ряда 3, 4, 5, ….. и N2 = 3 система уравнений (2) определяет бесконечный ряд многогранников конической (пирамидальной) формы, который начинается правильным многогранником – тетраэдром, являющимся одним из тел Платона. При стремлении N1 к бесконечности этот ряд тел, задаваемый системой уравнений (2) стремится к гладкому конусу. Примеры рассматриваемых геометрических тел приведены на рисунке ниже:

При целых значениях N1 из ряда 3, 4, 5, ….. и N2 = 4 система уравнений (2) определяет бесконечный ряд многогранников - призм, который начинается правильным многогранником – кубом, являющимся одним из тел Платона. При стремлении N1 к бесконечности этот ряд тел, задаваемый системой уравнений (2) стремится к гладкому цилиндру. Примеры рассматриваемых геометрических тел приведены на рисунке ниже:

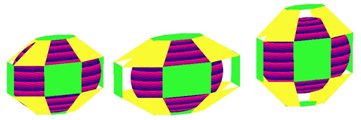
При L1 = L2 и N1 и N2 принимающих целые значения из ряда 5, 6, 7, … система уравнений (2) определяет бесконечный ряд многогранников, стремящийся к гладкой сфере при стремлении коэффициентов N1 и N2 к бесконечности. Примеры рассматриваемых геометрических тел приведены на рисунке ниже:
Очевидно, что при всех нечетных значениях N2 одно из оснований многогранника всегда будет иметь выступающий угол ("шатровую часть"), как у двух первых многогранников на рисунке выше, а при всех четных значениях N2 два плоских параллельных друг другу основания, как у третьего многогранника на рисунке выше.
При L1 = L2 всегда можно вписать сферу в многогранник, построенный по системе уравнений (2), как это показано для первого многогранника на рисунке ниже. При L1 > L2 многогранник растягивается в горизонтальной плоскости относительно вписанной сферы, как это показано для второго многогранника на рисунке ниже. При L1 < L2 многогранник растягивается в вертикальной плоскости относительно вписанной сферы, как это показано для третьего многогранника на рисунке ниже.
На рисунке выше часть граней в многогранниках была удалена для того, чтобы было видно вписанные в многогранники сферы.
При неравных между собой L1 и L2 и стремлении N1 и N2 к бесконечности ряд геометрических тел, задаваемых системой уравнений (2), будет стремиться не к сфере, а к гладкому эллипсоиду.
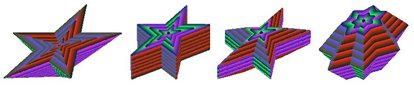
Для всех N1 представленных числами с дробной частью система уравнений (2) определяет бесконечный ряд звездчатых (самопересекающихся) многогранников примеры, которых приведены ниже на рисунке:
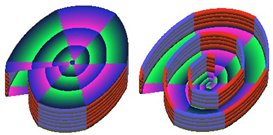
Если при формировании системы уравнений (2) вместо выражения, описывающего в полярных координатах многоугольники применить аналогичное уравнение, но описывающее спирали, то такая видоизмененная система уравнений (2) будет описывать уже геометрические тела типа улиток. Пример, улитки приведен на рисунке ниже. Причем второй рисунок выполнен со срезанным верхом для того, чтобы была видна внутренняя спиральная поверхность.
октябрь 2008 года