
| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
Описание уравнениями таких геометрических фигур, как четырехугольники (квадрат, прямоугольник, параллелограмм, трапеция и др.) стало возможным с появлением так называемого универсального уравнения (смотрите статью "Уравнения многоугольников и спиралей на их основе" http://stob2narod.ru/3s.htm). Однако, как известно, четырехугольник представляет собой замкнутую ломаную линию. Это если речь идет лишь о его контуре, а если имеется в виду весь четырехугольник полностью, то он вообще представляет собой часть плоскости ограниченной замкнутой ломаной линией. Из-за этого обстоятельства часто описание вида: y=f(x) четырехугольника удается представить только как многозначную функцию.
Известно, что можно выражать многозначные функции посредством однозначных в случае их параметрического представления, т. е. выражения функциональной зависимости между несколькими переменными через вспомогательные переменные – параметры: x=f(t), y=f(t), где t некий параметр.
Совместное использование параметрического представления и универсального уравнения действительно позволило получить описания различных четырехугольников и не только четырехугольников в параметрическом виде. Ниже приведены примеры таких описаний.
Любой прямоугольник может быть однозначно задан системой параметрических уравнений (1).

В случае если L=3,14/4, то система уравнений (1) описывает квадраты разного размера в зависимости от величины заданной диагонали Р. В общем случае система уравнений (1) определяет графики в виде различных прямоугольников примеры, которых приведены ниже на рисунке:
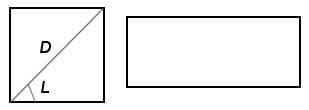
В системе уравнений (1) и в последующих уравнениях данной статьи выражения для вычисления коэффициентов А1…А4 выполняют роль ключей, обеспечивающих изменение хода вычислений по мере изменения величины параметра Т, а выражение для коэффициента А5 периодическую функцию на основе универсального уравнения (смотрите статью: Периодические импульсные функции на основе универсального уравнения http://stob2narod.ru/16s.htm ), обеспечивающую трансформацию непрерывного возрастания величины параметра Т в периодическое с шагом равным Р.
Прямоугольник представляет собой частный случай параллелограмма и соответственно сам является одновременно параллелограммом. Параллелограмм в общем случае может быть получен путем деформирования изначального прямоугольника.
Любой параллелограмм может быть однозначно задан системой параметрических уравнений (2), которое было получено из системы уравнений (1) путем введения в нее величины деформирования.

В общем случае система уравнений (2) определяет график в виде параллелограмма пример, которого приведен ниже на рисунке:
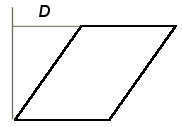
Очевидно, что если D=0, то система уравнений (2) будет определять параллелограмм в виде прямоугольника.
Если изначальный прямоугольник деформировать на величину D одновременно с двух сторон, то будет получена равнобедренная трапеция. Равнобедренная трапеция однозначно задается системой уравнений (3), которая была получена из системы уравнений (1) путем введения двусторонней деформации.
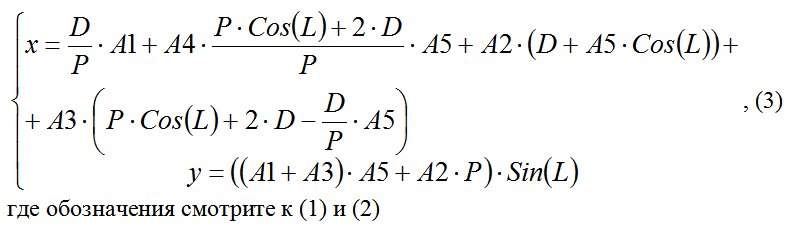
В общем случае система уравнений (3) определяет график в виде равнобедренной трапеции пример, которого приведен ниже на рисунке:
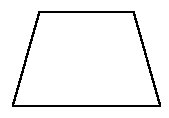
Необходимо отметить, что вид графиков, получаемых при помощи уравнений (1) – (3) очень сильно зависит от принимаемого значения L. Особенно сильна эта зависимость у системы уравнений (3). Ниже в таблице приведен ряд изменений вида графика, заданного системой уравнений (3) по мере изменения значения L.

Приведенные выше в таблице виды графиков в свою очередь зависят от изменения величины P. При составлении таблицы P оставалось неизменным и равным 100.
Исследовать свойства систем уравнений (1) – (3) можно при помощи специальной компьютерной программы: Программа исследования уравнений четырехугольников: прямоугольника, параллелограмма, трапеции: http://stob2.narod.ru/zetirexygol/zetirexygol.exe .
До сих пор речь шла лишь об описании ломанной линии контура четырехугольников, но аналогичными уравнениями можно описывать и всю площадь занимаемую четырехугольником. Ниже приведены примеры систем уравнений задающих такие прямоугольники (4) и параллелограммы (5).

Ниже на рисунке приведены примеры четырехугольников построенных при помощи систем уравнений (4) и (5).

Смотрите так же статью: "Уравнение правильных многоугольников в полярных координатах" (http://stob2narod.ru/27s.htm).
август 2009 года