
Рис. 29 Литография М. Эшера "Водопад"
| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
В определенном смысле эта статья является продолжением статьи "Невозможные фигуры – порнография в искусстве. Математическое описание невозможных фигур". Поэтому перед ознакомлением с данной статьей целесообразно прочитать первую статью, находящуюся по адресу: http://stob2.narod.ru/9s.htm .
Считается, что невозможные фигуры лишь создают впечатление трехмерного объекта, и это подразумевает, что такой объект вполне возможно вращать и рассматривать его с различных углов. Но при вращении трехмерной модели (причем неважно физической или виртуальной) сразу станут, видны все щели и изгибы в модели, без которых считается невозможным создание трехмерной модели невозможной фигуры. Поэтому в целях сокрытия этих щелей и изгибов необходимо все время по мере вращения трехмерной модели изменять ее геометрию.
Однако насколько верны все эти утверждения? Ведь в статье: "Невозможные фигуры – порнография в искусстве. Математическое описание невозможных фигур" было убедительно показано, что для получения невозможной фигуры вовсе необязательно в ее трехмерной модели (3D модели) делать прорези и изгибы или еще каким-либо образом изменять геометрию модели. Достаточно лишь частично изменить очередность проецирования точек поверхности 3D модели на плоскость. Или, если говорить иначе практически речь идет о частичном изменении окраски поверхности 3D модели без фактического изменения местоположения точек поверхности 3D модели в трехмерном пространстве.
Для того чтобы убедиться, что это действительно так ниже приведены анимации невозможных объектов (фигур). На них видно, что используемые при создании анимации трехмерные модели (3D модели) действительно не имеют прорезей, изгибов или иных геометрических деформаций.
Для лишения возможности скептиков заявить о том, что в данной статье рассмотрено создание лишь малоизвестных невозможных фигур, а для классических невозможных фигур предлагаемый метод их создания, возможно, работать и не будет, здесь рассмотрены анимации в основном широко известных, если так можно выразиться, классических невозможных фигур.
Кроме этого необходимо отметить, что повторить все увиденное в данной статье при помощи обычных стандартных графических 3D редакторов практически невозможно. Для создания трехмерных моделей невозможных фигур необходим графический 3D редактор, способный работать с каждой отдельной точкой поверхности модели независимо от остальных точек. Ознакомиться с математическими принципами работы такого специфического 3D графического редактора можно в статье: "Точечная графика: запись математической формулой".
Для непосредственного ознакомления с анимацией конкретной невозможной фигуры необходимо перейти по приведенным ниже ссылкам. Каждая ссылка загружает анимацию соответствующую своему названию.
1. Анимация невозможного треугольника
3. Анимация невозможного прямоугольника
5. Анимация невозможной спирали
6. Анимация невозможного цилиндра
7. Анимация невозможной фигуры, составленной из двух невозможных прямоугольников
Приведенные примеры анимации невозможных фигур позволяют сделать ряд выводов:
Иллюзия невозможности существования в трехмерном пространстве любой нормальной объемной фигуры может быть достигнута путем полного или частичного проецирования точек поверхности объемной фигуры на плоскость в обратном порядке, т. е. путем отображения на плоскость ближних к наблюдателю точек первыми, а дальних последними. Или можно сказать иначе – путем изменения окраски трехмерной модели отображаемой на плоскость геометрической фигуры.
Для получения иллюзии невозможности существования в трехмерном пространстве какой-либо геометрической фигуры вовсе не обязательно делать в ее трехмерной модели, как в реальной, так и в виртуальной, какие-либо прорези и изгибы, скрываемые от наблюдателя. В качестве трехмерной модели любой невозможной фигуры всегда можно использовать нормальную, без каких-либо геометрических деформаций, объемную геометрическую фигуру, т. е. нормальные геометрически не измененные треугольники, прямоугольники, кольца, кубы и т. д.
Изменив один раз окраску трехмерной модели невозможной фигуры, в ходе ее дальнейшего вращения всегда будет создаваться иллюзия невозможности ее существования в трехмерном пространстве. Правда иллюзия невозможности фигуры не всегда будет очевидной и хорошо заметной для наблюдателя.
Необходимо отметить, что фактически окраска трехмерной модели фигуры не изменяется, т. е. трехмерная модель остается абсолютно нормальной и в части ее окраски, во всяком случае, в трехмерном пространстве. Изменяется окраска ее отображения. Или, если, как любят говорить топологи, мы видим некое подобие того, что мы бы увидели, взглянув на реально существующую в трехмерном пространстве геометрическую фигуру из четвертого измерения. Именно в четвертом измерении точки противоположных сторон нашей фигуры как бы склеиваются и при наблюдении за ними меняются местами, что, собственно, на отображениях в двухмерное пространство и порождает иллюзию невозможности.
В некоторых случаях невозможность геометрической фигуры становится очевидной только при просмотре анимации ее вращения, а при просмотре отдельных кадров анимации она остается незаметной для наблюдателя.
Любой реально существующий трехмерный геометрический объект может быть представлен в качестве невозможного. Это утверждение справедливо и для совсем простых по своей форме геометрических фигур, например, таких как шар или куб.
Как следует из материалов данной статьи, получение изображений невозможных геометрических фигур происходит строго в соответствии с законами геометрии и топологии. Если на основе этих законов написать специальную компьютерную программу, то получать изображения невозможных геометрических фигур можно будет в автоматическом режиме и практически без участия человека. И тогда возникает вопрос: А какое, собственно говоря, отношение все это имеет к искусству?
Здесь этот вопрос задан, прежде всего, в отношении художественного течения называемого имп-арт (imp-art, impossible art), в основе которого лежит именно изображение невозможных геометрических фигур.
Другое дело, когда изображение невозможно не только геометрически, но и физически. Ряд примеров таких изображений показано на Рис. 29-32


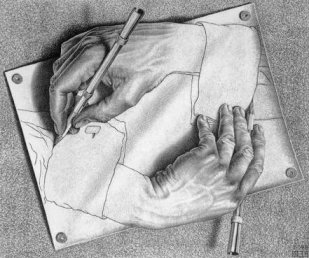

На этих изображениях невозможные геометрические фигуры используются в лучшем случае в качестве основы для прорисовки воды, текущей физически невозможным образом, физически невозможных элементов зданий, физически невозможного перехода руки в плоский рисунок и т. п. Конечно, сами по себе реалистичные изображения объектов окружающего мира вполне могут быть отнесены к произведениям искусства. Ведь для создания таких изображений в той или иной мере, но художника привлекать все же придется. Нарисовать принципиально новые подобные изображения, как графики некоторых функциональных зависимостей пока вряд ли получится. Хотя чисто математически описать их после создания уже можно. А вот невозможные геометрические фигуры выводить на принтер как графики функциональных зависимостей можно уже сейчас, что очень хорошо было показано на примерах приведенных в этой статье анимации различных невозможных геометрических фигур.
Однако выделять произведения искусства с физически невозможными изображениями в самостоятельное направление изобразительного искусства вряд ли целесообразно. Хотя бы уже потому, что они очень похожи на произведения сюрреализма. Для сравнения далее приведены некоторые произведения известных сюрреалистов.



На картинах (Рис. 33-34) точно так же, как и на изображениях (Рис. 31-32) показаны физически невозможные переходы плоских изображений в объемные тела. На Рис. 35 мужчина смотрит в зеркало, в котором отражается его затылок и спина, что физически невозможно. И этот прием отображения уже совсем близок к тому, каким образом в данной статье были получены все без исключения невозможные геометрические фигуры.
Вообще в творчестве художников сюрреалистов физически невозможные изображения встречаются достаточно часто и многие из них были созданы еще до появления первого невозможного треугольника и последовавших за ним других невозможных объектов.
декабрь 2011 года