| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
НЕВОЗМОЖНЫЕ ФИГУРЫ – ПОРНОГРАФИЯ В ИСКУССТВЕ
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕВОЗМОЖНЫХ ФИГУР
А.М. Белов
Со времени выхода в британском журнале психологии статьи Роджера и Лайонела Пенроузов о невозможных фигурах (1958 год) было напечатано множество подобных материалов, а еще больше всяческих невозможных фигур было нарисовано, как до появления статьи, так и после ее опубликования. В настоящее время, наверное, уже не возможно собрать все эти фигуры в одном месте. Да, и появляются новые невозможные фигуры буквально каждый день. Сейчас даже не возможно установить с абсолютной надежностью, что только нарисованная в данный момент фигура является действительно новой, а не вариантом уже давно где-то кем-то нарисованной невозможной фигуры.
Учитывая, сложившуюся ситуацию в рассматриваемой сфере человеческого творчества и, что бы не тратить время читателя на просмотр информации с большой вероятностью, не являющейся для него новой, в этой статье не приводятся традиционные широко известные невозможные фигуры типа невозможного треугольника, бесконечной лестницы и т. п. Действительно очень трудно представить себе человека, который за всю свою жизнь ни разу не видел изображения невозможного треугольника. Если все же такой человек найдется, то он без особого труда сможет ознакомиться с этими невозможными фигурами и без этой статьи, да и, скорее всего этому человеку и эту статью читать не надо.
Несмотря на значительное количество публикаций о невозможных фигурах их четкого определения по существу не сформулировано. Можно прочесть, что к невозможным фигурам относятся все оптические иллюзии, связанные с особенностями нашего восприятия мира. С другой стороны человек может показать Вам фигуру человека зеленого цвета или с десятью руками и пятью головами и сказать, что все это невозможные фигуры. При этом он будет по своему прав. Ведь людей зеленого цвета с десятью ногами не бывает. По этому в данной статье под невозможными фигурами будут пониматься плоские изображения фигур воспринимаемые человеком однозначно, как они нарисованы без восприятия человеком каких бы то ни было дополнительных, фактически не нарисованных изображений или искажений и которые не возможно представить в трехмерном виде. Невозможность представления в трехмерном виде понимается, конечно, только непосредственная без учета возможности применения специальных средств при изготовлении невозможных фигур, т. к. всегда невозможную фигуру можно изготовить, применив хитроумную систему прорезей, дополнительных поддерживающих элементов и изгибания элементов фигуры, а затем сфотографировав ее под нужным углом.
Таким образом, в данной статье не рассматриваются фигуры людей зеленого цвета с пятью головами и фигуры подобные таким, так же не рассматриваются чисто оптические иллюзии. С гипотезой возникновения у человека оптических иллюзий можно ознакомиться в статье "А, робот должен видеть сны?".
Приведенное здесь определение невозможных фигур, да и другие известные определения не дают четкого ответа на вопросы: Чем же все же принципиально отличается невозможная фигура от всех прочих? Что нужно обязательно сделать, что бы нарисовать именно невозможную фигуру? Чисто интуитивно мы конечно практически без ошибок классифицируем фигуры, но это все происходит примерно на том же уровне, как мы разделяем людей по внешности с первого взгляда на приятных и на неприятных. Существует множество описаний способов и инструкций получения невозможных фигур, но все они носят все же не общий характер, а частный и применимы лишь к отдельным видам невозможных фигур или к фигурам, составляемым из отдельных строго определенных элементов.
Для получения общего всеобъемлющего ответа на поставленные вопросы необходимо получить чисто математическое описание в общем, виде любой невозможной фигуры.
В статье "Точечная графика: запись математической формулой" было предложено универсальное уравнение способное описать практически любой объект или его изображение. Уравнение представляет собой сумму выражений:
[xi/x]*[x/xi]* [yi/y]*[y/yi]* [zi/z]*[z/zi]*t, где
x, y, z - текущие координаты в трехмерном пространстве;
xi, yi, zi – координаты i-ой точки объекта;
t – число, задающее цвет i- ой точки объекта, например код в системе RGB;
[ ] – знак, обозначающий целую часть числа.
Общее количество слагаемых в уравнении определяется максимальным значением i или количеством точек, на которые разбит описываемый объект. При подстановке в уравнение значений координат x, y, z все время будут получаться нули, пока координаты не совпадут с координатами xi, yi, zi какой либо точки объекта и тогда будет получено значение t.
Поскольку предложенное универсальное уравнение способно описать практически любой объект, то нет ни каких препятствий для описания при помощи универсального уравнения и невозможных фигур. Рассмотрим такое описание на примере простого объекта состоящего всего из двух точек красного и синего цвета. Зададим его уравнением:
q=[5/x]*[x/5]*[2/y]*[y/2]*[7/z]*[z/7]*255001001+ - точка красного цвета
+[5/x]*[x/5]*[9/y]*[y/9]*[7/z]*[z/7]*001001255 - точка синего цвета
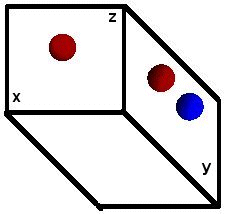
При последовательной подстановке в это уравнение x, y, z соответственно их значений от нуля до бесконечности для построения проекций точек на плоскости (xz) и (yz) мы ничего необычного не заметим, но стоит нам изменить на обратный порядок подстановки значений x, y, z, т. е. от бесконечности до нуля мы увидим, как это показано на приведенной ниже схеме, что, на проекции на плоскость (xz) вперед вышла точка красного цвета, что в трехмерном представлении невозможно без фактического изменения расположения точек. При этом проекция на плоскость (yz) выглядит нормально и точка синего цвета, отстоящая от начала координат на 9 единиц по оси y, находится ближе к наблюдателю, чем точка красного цвета, отстоящая от начала координат по оси y на 2 единицы согласно уравнению.

Таким образом, проекция на плоскость (xz) представляет собой невозможную фигуру. Конечно, с чисто художественной точки зрения проку от такой невозможной фигуры мало. По этому такие фигуры и не рисуют. Нет зрелищности. Однако, эта фигура замечательна тем, что является элементарной и из подобных фигур теоретически можно собрать любую более сложную и зрелищную невозможную фигуру. Точно так же как любое изображение (объект) можно представить в виде набора точек.
Рассмотренный пример позволяет сформулировать следующее необходимое и достаточное условие для получения произвольной невозможной фигуры: При формировании невозможной фигуры в виде проекции объекта на плоскость необходимо полностью или часть точек объекта вывести в обратной последовательности, т. е. самые близкие точки объекта к наблюдателю первыми, а самые дальние от наблюдателя точки последними.
Таким образом, при рисовании невозможной фигуры, мы осознанно или неосознанно, делаем все неправильно и наоборот, и в этом смысле невозможные фигуры можно назвать порнографическими. Конечно, при этом слово порнография использовано в переносном своем значении, не усматривается никакого эротического содержания в фигуре и, не имеются в виду невозможные фигуры изображающие непристойное выполнение полового акта.
Читать о картинках конечно интересно, но еще интереснее их рассматривать и в данном случае в полной мере применимо правило: лучше один раз увидеть, чем сто раз услышать. Поэтому перейдем к рассмотрению использования сформулированного выше условия на примерах конкретных картинок.
Возьмем в качестве исходного объекта обычный спичечный коробок. Создадим его трехмерную модель, например, с помощью графического редактора, приведенного в статье "Точечная графика: запись математической формулой" и, следуя сформулированному условию при выведении проекции этого коробка точки, формирующие одну из сторон этого коробка (самую дальнюю для наблюдателя) выведем поверх всех остальных точек изображения. Внимательно рассмотрев получившуюся в результате фигуру можно без труда прийти к выводу, что в трехмерном пространстве такая фигура невозможна, т. е. применение, сформулированного выше условия привело к созданию невозможного спичечного коробка:

Необходимо отметить, что хотя применение необходимого и достаточного условия получения произвольной невозможной фигуры при построении проекции практически любого трехмерного объекта приводит к созданию невозможной фигуры наглядность (заметность) этого все же зависит от точки просмотра этого объекта (угла под которым он проецируется на плоскость). Это утверждение хорошо иллюстрируют, приведенные ниже два рисунка.


На обоих рисунках проекции левых коробков были сформированы в нормальном правильном режиме, а проекции правых коробков были получены полностью путем выведения точек изображения коробков в обратном порядке, т. е. ближние к наблюдателю точки выводились первыми, а дальние последними. В результате дальние от наблюдателя точки полностью закрыли ближние к наблюдателю точки изображения. Кроме этого нижний рисунок был получен путем поворота трехмерной модели первого примерно на 45 градусов, что позволило изменить угол проецирования коробков и стола на плоскость.
Оба рисунка представляют собой невозможные фигуры. Однако заметить это на первом рисунке может только очень внимательный зритель по ненормальной интенсивности освещения коробков, а вот изменение угла проецирования для второго рисунка обеспечило наглядность его невозможности в трехмерном представлении.
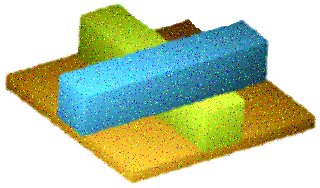
В некоторых случаях более заметным невозможность представления в трехмерном виде, изображенных на плоскости предметов делает размещение рядом других объектов или разметок, как это можно наблюдать на размещенном ниже рисунке.

Так же невозможность изображения может подчеркиваться тенями и интенсивностью освещения. На приведенном ниже рисунке, представляющем собой невозможную решетку из карандашей, ровное освещение поверхности карандашей и прямые ровные тени от карандашей однозначно нам подсказывают, что карандаши на рисунке изображены действительно проходящими друг через друга, а не изогнутыми. Если бы карандаши были изогнутыми, то фигура из них в принципе могла бы быть представлена в трехмерном пространстве.

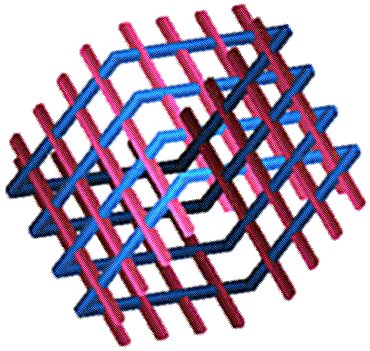
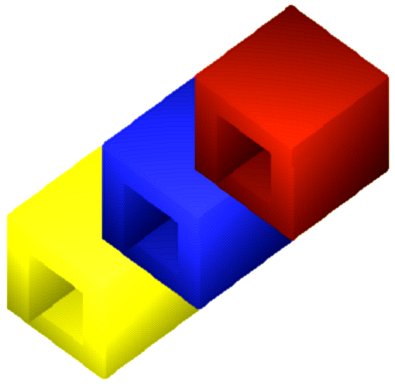
Эффект невозможности фигуры в большей степени заметен на не сплошных фигурах составленных из отдельных элементов (брусков, трубок, стержней и т. п.). Возможно, именно по этой причине большую часть невозможных фигур обычно набирают из отдельных элементов. Пример такой "наборной" невозможной фигуры, созданной с использованием необходимого и достаточного условия получения произвольной невозможной фигуры, приведен ниже на рисунке:
Далее приведен целый ряд невозможных фигур, который показывает, что тип невозможной фигуры практически не влияет на применимость необходимого и достаточного условия получения произвольной невозможной фигуры.

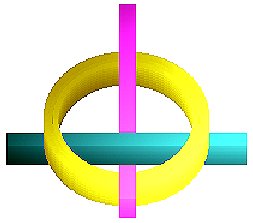

Несколько отдельных разнотипных невозможных фигур в свою очередь могут объединяться в одну. При этом сложность такой невозможной фигуры может возрастать до бесконечности. Пример подобной невозможной фигуры приведен на рисунке ниже.

Последовательное применение необходимого и достаточного условия получения произвольной невозможной фигуры к кадрам анимации позволяет получать анимации невозможных фигур. Ниже приведены примеры двух, таким образом, полученных анимаций. На первой анимации обычный спичечный коробок превращается в невозможный и обратно при совершении вращательных колебании от 0 до 90 градусов и обратно. На второй анимации конструкция из двух спичечных коробков совершает вращательные колебания от 0 до 180 градусов и обратно, а наблюдателю кажется, что только от 0 до 90 градусов. При этом передние и задние (для наблюдателя) стенки коробков периодически постепенно меняются местами.


Можно отметить еще одну интересную особенность невозможных фигур. Считается, что в плоском двумерном пространстве невозможная фигура реальна и не может быть реализована в трехмерном пространстве. Однако невозможная фигура может быть реализована так же и в пространствах имеющих число измерений большее трех. Правда, такая реализация пока возможна только чисто математически в виде уравнений, описывающих невозможную фигуру. Ведь пока только уравнения допускают одновременное размещение нескольких объектов в одном и том же трехмерном объеме и перевод отдельных объектов в разряд фактически невидимых в отдельных пространствах или подпространствах.
Описанная в настоящей статье методика создания невозможных фигур позволяет получать невозможные фигуры из трехмерных моделей любых объектов практически в автоматическом режиме. Из сказанного так же следует, что количество невозможных фигур практически бесконечно. Использование же той или иной невозможной фигуры ее распространенность будет зависеть исключительно от ее художественной ценности (зрелищности), уместности ее использования в логотипе, знаке или рекламе.
октябрь 2004 года