| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |

            В статье «О нумерологии, лженауке, математике, формуле и калькуляторе нумерологического сокращения чисел» http://stob2.narod.ru/36s.htm был рассмотрен вопрос о чисто математических предпосылках возможности делать прогнозы по нумерологически сокращенным числам.

            Для рассмотрения этого вопроса была получена формула нумерологического сокращения чисел на основе процедуры замены исходного числа его остатком от целочисленного деления по некоторому модулю. Для целей нумерологии модуль наиболее часто имеет значение – 9, но может принимать и иные значения. То есть были использованы методы арифметики вычетов, которую часто еще называют модульной арифметикой или модулярной арифметикой.

            Формула, выполняющая процедуру замены исходного числа его остатком от целочисленного деления на модуль, выглядит следующим образом:

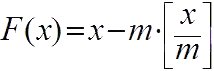
            где x – значение нумерологически сокращаемого натурального числа; m – модуль; [ ] – знак, обозначающий целую часть числа или обозначает операцию по отбрасыванию дробной части от результата вычисления выражения, стоящего в прямоугольных скобках.

            Необходимо отметить, что в арифметике вычетов эту процедуру по непонятным причинам предпочитают задавать не в виде формулы, а словесными формулировками.

            Данная формула задает периодическую импульсную функцию. Такие функции известны уже сравнительно давно. О методах их задания можно посмотреть в статье: Периодические импульсные функции на основе универсального уравнения http://stob2.narod.ru/16s.htm .

            То, что рассматриваемая формула выполняет процедуру замены исходного числа его остатком от целочисленного деления на модуль m и тем самым задает периодическую импульсную функцию, показывает очевидность возможности преобразования с помощью этой формулы ряда натуральных чисел в бесконечно повторяющуюся последовательность чисел следующего вида: 1, 2, …, m – 1, 0, 1, 2, …, m – 1, 0, ….

            В теории сравнений предусмотрена возможность разбиения множества натуральных чисел на m групп относительно m, в которых элементы одной и той же группы будут иметь одинаковые вычеты по модулю m. Но и только. А вот возможность преобразования ряда натуральных чисел в ряд вида: 1, 2, …, m – 1, 0, 1, 2, …, m – 1, 0, … не рассматривается. Соответственно из теории сравнений было исключено нумерологическое положение Пифагора о рассматривании цифр от 1 до 9 в качестве исходных, из которых могут быть получены все остальные числа. То есть преобразование ряда: 1, 2, …, m – 1, 0, 1, 2, …, m – 1, 0, … обратно в ряд натуральных чисел даже не рассматривалось.

            И это неудивительно, так как в ряде: 1, 2, …, m – 1, 0, 1, 2, …, m – 1, 0, … систематически появляется ноль, который препятствует получению достаточно элементарной и очевидной формулы преобразования этого ряда в ряд натуральных чисел. А вот при выполнении процедуры нумерологического сокращения чисел подобная проблема не может даже возникнуть.

            Таким образом, получается, что арифметика вычетов и нумерологическое сокращение чисел являются разными математическими процедурами и арифметика вычетов никак не может заменить нумерологическое сокращение чисел.

            Но если формулу, выполняющую процедуру замены исходного числа его остатком от целочисленного деления на модуль m дополнить выражениями, позволяющими в ходе выполнения вычислений ноль заменять значением выбранного модуля m, то можно получить полностью соответствующую процедуре нумерологического сокращения чисел формулу:

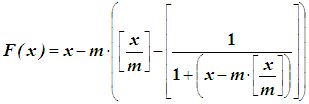
            где x – значение нумерологически сокращаемого натурального числа; m – модуль; [ ] – знак, обозначающий целую часть числа или обозначает операцию по отбрасыванию дробной части от результата вычисления выражения, стоящего в прямоугольных скобках.

            Данная формула так же задает периодическую импульсную функцию и позволяет преобразовывать ряд натуральных чисел в бесконечно повторяющуюся последовательность чисел следующего вида: 1, 2, …, m, 1, 2, …, m, …. То есть данная периодическая функция в пределах каждого своего периода последовательно принимает значения от 1 до m. При этом, как и в случае классического нумерологического сокращения чисел, появление в получающейся последовательности чисел нуля практически невозможно.

            Необходимо отметить, что полученная формула, в отличие от представлений Пифагора о возможности сокращения любого числа до цифр от 1 до 9 включительно, указывает на возможность выполнения нумерологического сокращения от 1 до любого числа.

            Кроме этого отсутствуют, какие либо проблемы с составлением формулы для преобразования числового ряда: 1, 2, …, m, 1, 2, …, m, …. в ряд натуральных чисел. Действительно она может быть записана в виде очень простого выражения:

            A = m · N – m + F,

            где A – исходное число до нумерологического сокращения; N – порядковый номер периода в числовом ряде: 1, 2, …, m, 1, 2, …, m, …. (Данный числовой ряд в пределах каждого своего периода последовательно принимает значения от 1 до m.); F – нумерологическое число из ряда 1, 2, …, m; m – модуль нумерологического сокращения числа.

            Приведем пример применения данной формулы.

            Допустим, необходимо узнать какое число A натурального ряда будет соответствовать нумерологическому числу F = 9 из периода N = 111 по модулю m = 9. Для этого подставляем F = 9, N = 111 и m = 9 в формулу и производим вычисления:

            А = 9 · 111 – 9 + 9 = 999

            Проверяем, действительно ли, получившееся в ходе вычислений, число А = 999 нумерологически сокращается до F = 9: 9 + 9 + 9 = 27 (2 + 7 = 9).

            Необходимо обратить внимание на то, что если бы число 999 сокращалось бы методами арифметики вычетов, то есть заменялось бы его остатком от целочисленного деления на модуль m = 9, то было бы получено значение нумерологического числа F не девять, а ноль. Такое изменение значения числа F в свою очередь приведет к вычислению при помощи рассматриваемой формулы неверного значения числа А = 9 · 111 – 9 + 0 = 990.

            Таким образом, все числа натурального ряда могут быть получены не только из ряда чисел от 1 до 9, но и из любого подобного ряда чисел, а минимальный ряд таких чисел состоит всего из двух чисел – единицы и двойки.

            Действительно, бесконечный числовой ряд: 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, …. при помощи рассмотренных формул преобразуется в бесконечный числовой ряд вида: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …., то есть фактически в натуральный ряд чисел. А вот числовой ряд, состоящий из одних единиц, уже не будет выражать периодическую функцию, и преобразовывать его станет невозможно.

            Таким образом, является очевидным, что члены бесконечных числовых рядов 1, 2, …, m, 1, 2, …, m, …. и 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,… взаимно связаны, и один ряд может быть всегда преобразован в другой.

            Поскольку нумерологическое сокращение осуществляется путем сложения всех цифр сокращаемого числа, то числа натурального ряда и соответствующие им нумерологические числа F (от 1 до m) будут показывать схожие свойства при совершении с ними в первую очередь операций сложения.

            Это означает, что при выполнении операций сложения можно отказаться от непосредственного использования в ходе вычислений больших чисел и заменить большие числа, на числа F, получаемые при нумерологическом сокращении (фактически на числа от 1 до m) и при этом получить качественно (но не количественно) практически идентичный результат. Иначе говоря, все изменения свойств, полученные при выполнении операций сложения с числами F от 1 до m, могут быть распространены на все числа соответствующие этим числам F в ряду натуральных чисел.

            К операциям сложения можно отнести не только собственно само сложение, но и операцию умножения, и операцию возведения в степень. Так как умножение можно заменить повторением операций сложения, например: 4 · 5 = 20 (4 + 4 + 4 + 4 + 4 = 20) или 3³ = 27 3 · 3 · 3 = 27 (3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 27).

            Рассмотрим сложение двух произвольных чисел A₁ = m · N₁ – m + F₁ и A₂ = m · N₂ – m + F₂, представленных с использованием соответствующих им нумерологических чисел F.

            A₃ = A₁ + A₂ = m · (N₁ + N₂) – 2 · m + F₁ + F₂

            Полученное выражение для вычисления суммы чисел A₁ и A₂ может быть приведено к виду: A₃ = m · N₃ – m + F₃, где

            N₃ = N₁ + N₂ – 1 + [(F₁ + F₂) / (1 + m)],

            где в свою очередь [ ] – знак обозначающий целую часть числа или обозначает операцию по отбрасыванию дробной части от результата вычисления выражения, стоящего в прямоугольных скобках; F₃ – результат нумерологического сокращения суммы чисел F₁ и F₂ по модулю m.

            Из выражения для вычисления значения A₃ суммы чисел A₁ и A₂ следует, что не только результат F₃ нумерологического сокращения числа A₃ по модулю m в обязательном порядке должен быть равен результату нумерологического сокращения суммы чисел F₁, F₂,… F_k по тому же значению модуля m, но и порядковый номер периода N₃ обязательно должен быть равен одному из следующих значений сумм: N₁ + N₂ + …+ N_k, N₁ + N₂ + …+ N_k – 1,… N₁ + N₂ + …+ N_k – (k – 1), где k – количество слагаемых в сумме A₁ + A₂ + ….

            Поясним это утверждение при помощи конкретных числовых примеров.

            Вычислим сумму трех произвольных чисел: 5 + 12 + 71 = 88. Теперь произведем нумерологическое сокращение, например, по модулю m = 7 каждого из этих чисел и определим соответствующие им номера периодов в бесконечной числовой последовательности 1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7,…. В результате для 5 получим F₁ = 5 и N₁ = 1, для 12 получим F₂ = 5 и N₂ = 2, для 71 получим F₃ = 1 и N₃ = 11 и для 88 получим F₄ = 4 и N₄ = 13.

            Число 4, являющееся результатом нумерологического сокращения по модулю m = 7 суммы чисел F₁ + F₂ + F₃ = 5 + 5 + 1 = 11 окажется равно F₄ = 4. И это правило будет выполняться всегда независимо от количества слагаемых и способов выполнения сложения (тут имеются в виду операции умножения и возведения в степень).

            А порядковый номер периода N₄ = 13 = N₁ + N₂ + N₃ – 1 = 1 + 2 + 11 – 1 = 13. Это правило будет так же выполняться всегда независимо от количества слагаемых. Правда, необходимо отметить, что возможное значение периода N все же в небольших пределах будет зависеть от количества слагаемых.

            Поскольку бесконечный ряд натуральных чисел всегда может быть преобразован в бесконечный периодический числовой ряд 1, 2, …, m, 1, 2, …, m, …., то свойства чисел натурального ряда соответствующие числам ряда 1, 2, …, m, 1, 2, …, m, …. тоже периодически будут повторяться. Поэтому свойства чисел натурального ряда, соответствующие числам первого периода числового ряда 1, 2, …, m, 1, 2, …, m, …. будут бесконечно воспроизводиться в последующих периодах, а, следовательно, появляется возможность делать оценку свойств сумм чисел определенного вида на протяжении всего бесконечного ряда натуральных чисел. Числовой ряд 1, 2, …, m, 1, 2, …, m, …. в пределах каждого своего периода последовательно принимает значения от 1 до m.

            Пример 1

            Возьмем два произвольных числа и сложим их между собой:

            47+58 = 105

            Произведем нумерологическое сокращение числа 47:

            4+7=11(1+1=2)

            Произведем нумерологическое сокращение числа 58:

            5+8=13(1+3=4)

            Произведем нумерологическое сокращение числа 105:

            1+5=6

            Теперь сложим числа, полученные после выполнения нумерологического сокращения:

            2+4=6

            И убедимся, что мы получили верное равенство и, что 105 нумерологически сокращается именно до 6.

            Выполнение операции сложения между обычными числами и числами, полученными в ходе нумерологического сокращения практически равнозначно, особенно если можно быстро перейти от нумерологически сокращенных чисел к исходным значениям чисел.

            Пример 2

            Возьмем два произвольных числа и перемножим их между собой:

            27*94=2538

            Произведем нумерологическое сокращение числа 27:

            2+7=9

            Произведем нумерологическое сокращение числа 94:

            9+4=13(1+3=4)

            Произведем нумерологическое сокращение числа 2538:

            2+5+3+8=18(1+8=9)

            Теперь перемножим числа, полученные после выполнения нумерологического сокращения:

            9*4=36(3+6=9)

            И убедимся, что мы получили верное равенство и, что 2538 нумерологически сокращается именно до 9.

            Выполнение операции умножения между обычными числами и числами, полученными в ходе нумерологического сокращения практически равнозначно, особенно если можно быстро перейти от нумерологически сокращенных чисел к исходным значениям чисел.

            Пример 3

            Возьмем произвольное число и возведем его в произвольную степень:

            29^4=707281

            Произведем нумерологическое сокращение числа 29:

            2+9=11(1+1=2)

            Произведем нумерологическое сокращение числа 707281:

            7+7+2+8+1=25(2+5=7)

            Теперь возведем в степень 4 число, полученное после выполнения нумерологического сокращения (число – 2):

            2^4=16(1+6=7)

            И убедимся, что мы получили верное равенство и, что 707281 нумерологически сокращается именно до 7.

            Выполнение операции возведения в степень обычного числа и числа, полученного в ходе нумерологического сокращения практически равнозначно, особенно если можно быстро перейти от нумерологически сокращенных чисел к исходным значениям чисел.

                                                                                                            октябрь 2014 года