| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
Нумерология - система, традиция или верование о мистических или эзотерических связях между числами и физическими объектами или живыми существами и их сознанием. Её часто называют магией чисел, хотя её концепция близка к астрологии и другим паранаукам древности. Нумерология и нумерологические гадания были популярны у ранних математиков, таких как пифагорейцы, и не считаются сейчас математическим знанием, как и в случае отделения алхимии от химии или астрологии от астрономии.
Ну и, наконец, говорят уже совсем прямо, что нумерология — это лженаука о числах.
Для тех, кто не совсем понимает, поясним – лженаука, она же псевдонаука, паранаука, квазинаука, альтернативная наука, неакадемическая наука, девиантная наука - мнимая или ложная наука, деятельность или учение, осознанно или неосознанно имитирующие науку, но, по сути, таковыми не являющиеся.
Наряду с нумерологией к лженауке обычно относят алхимию, астрологию, суперкритическую историографию или «новую хронологию», волновую генетику, торсионные поля, парапсихологию, телепатию, телекинез, психотронное оружие, экстрасенсорику, телегонию, графологию, валеологию, дианетику, соционику, френологию, гомеопатию и т. п.Само по себе составление подобного списка, необходимость указывать, что конкретно следует считать лженаукой, вообще-то плохой признак. Так как это указывает на то, что четких и однозначных критериев позволяющих отделить лженауку от собственно науки до сих пор не существует. В результате появляются глупые и абсурдные заявления. Так, например, можно обнаружить утверждение, что нумерология отрицает возможность опровержения своих выводов. Но нумерология не человек, а значит ни отрицать, ни подтверждать ничего не может. Это равносильно попытке доказать окружающим, что стул вам, что-то там сообщил. После такого настоящего ученого, борца с лженаукой уже и самого можно смело отправлять в психушку.
Однако сделать нормальный анализ нумерологии тоже не так просто, как это может показаться на первый взгляд. Ведь нумерология существует уже несколько тысячелетий. За это время в ее рамках успело потрудиться громадное количество людей, которые высказывали различные идеи и, соответственно, имели о ней разные представления. Далеко не все из наработанного было вообще опубликовано, а многое из опубликованного не всегда имеет приемлемый для привычного научного исследования вид. Поэтому на поиск и систематизацию положений всех ветвей нумерологии, а затем их объективную и строго научную проверку может потребоваться очень много времени. Возможно даже целая жизнь. Ясно, что тратить свою жизнь на все это никто не хочет. Вот и появляются сырые и звучащие глупо высказывания, а люди их, высказывающие, сами становятся похожи на лжеученых, плохо разбирающихся в объекте своей критики.
Пифагор, его ученики и последователи сократили все числа до цифр от 1 до 9 включительно, поскольку они являются исходными числами, из которых могут быть получены все другие. Для сокращения больших чисел в элементарные разработаны разные системы. Самый простой и популярный метод — сложить все цифры этого числа, затем, если образуется 10 или более, сложить и эти цифры, Этот процесс продолжают до тех пор, пока не получат элементарное число от 1 до 9. За каждой цифрой были закреплены определённые свойства, понятия и образы, исходя из которых, и составляется прогноз. Анализу могут быть подвергнуты любые числа: дата рождения, постройки судна, самолета, выпуска изделия, номер телефона, номер квартиры и т. д.
Именно эту систему, в том или ином виде, использует современная западная и русская школы нумерологии. В основном о ней в дальнейшем и будем говорить.
Числа в какой-то степени отражают связь предметов, явлений, процессов между собой, их взаимное влияние друг на друга. С нумерологической точки зрения, время движется по нескончаемо повторяющимся циклам от 1 до 9. Конечно, то, что в нашем мире абсолютно все взаимосвязано хорошо известно. Одно только существование законов сохранения очень хорошо это подтверждает. Другой вопрос насколько сильно это взаимное влияние, насколько детальным может быть прогноз развития того или иного процесса, насколько надежен может быть этот прогноз, удастся ли оценить влияние на конкретный объект суммы всех остальных объектов окружающего мира.
Теоретически оценить возможную точность нумерологического прогноза для отдельно взятого объекта можно по виду чисто математической функции нумерологического сокращения чисел. Конечно, это будет справедливо только для системы, состоящей всего из двух взаимовлияющих друг на друга объектов. По мере увеличения учитываемых в системе объектов точность прогноза будет повышаться в любом случае.
Поясним, о чем здесь идет речь, на примере. Допустим, метеоролог делает прогноз погоды в Москве на Красной площади через год 15 июля в два часа дня. Разумеется, при прогнозировании он будет исходить фактически только из даты и статистической информации и фактически сможет с очень большой вероятностью сказать, что температура воздуха будет выше нуля градусов и все. Если же он заявит, что температура воздуха составит 25,4 градуса, будет облачно и будет идти дождь, укажет конкретное значение направления и силы ветра, а также значение атмосферного давления, то будет очевидно, что точность такого прогноза будет не высока. А вот, если метеоролог будет составлять свой прогноз не за год, а за сутки, то он сможет учесть множество других, кроме даты и характерной для нее статистики, факторов, таких как фактически сложившееся распределение температур в окрестностях Москвы, направления и скорости воздушных потоков и т. д. В результате он сможет получить подробный прогноз, который сбудется с довольно высокой вероятностью.
Точно также, если при составлении нумерологического прогноза будет учитываться кроме, например, даты рождения, место рождения, время рождения, возраст родителей и т. д., то точность и информативность нумерологического прогноза значительно повысятся.
И еще, необходимо отметить, что как для метеопрогнозов, так и нумерологических прогнозов пока не удалось добиться стопроцентной надежности. Однако метеорологию не относят к лженаукам.
Для установления вида математической функции нумерологического сокращения чисел желательно иметь уравнение (формулу) нумерологического сокращения чисел. Как известно, таких уровней пока нет.
Составить уравнение, задающее функцию нумерологического сокращения чисел можно несколькими способами. Например, можно это сделать, как говориться «в лоб», т. е. записать в виде формулы алгоритм сокращения чисел, предложенный еще Пифагором. Тогда будет получено уравнение (1).
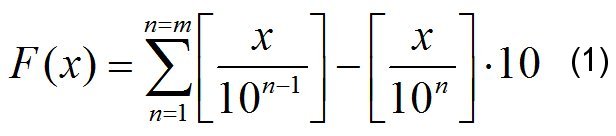
где x – значение сокращаемого числа (здесь и далее во всех формулах этой статьи); m – количество цифр в числе x; [ ] – знак обозначающий целую часть числа или обозначает операцию по отбрасыванию дробной части от результата вычисления выражения, стоящего в прямоугольных скобках (здесь и далее во всех формулах этой статьи).
Недостатком уравнения (1) является то, что оно не полное и не может нормально использоваться без введения дополнительных словесных пояснений. Так в случае, если при выполнении вычислений по уравнению (1) будет получено двухзначное и более число, то все вычисления по уравнению (1) придется повторить, но уже, с полученным в ходе предыдущего применения уравнения (1), числом. Конечно, уравнение (1) можно дополнить выражениями, которые позволят отказаться от использования словесных пояснений, и результат будет получаться в ходе прямых и непрерывных вычислений, но в любом случае такое уравнение будет слишком громоздким и сложным. Подобные формулы составлялись для вычисления простых чисел см. Теория чисел: простые числа и универсальное уравнение http://stob2.narod.ru/2s.htm
В математике встречается утверждение, что нумерологическое сокращение числа эквивалентно замене исходного числа его остатком от целочисленного деления на 9. То есть, предполагается, что процедура нумерологического сокращения числа может быть описана методами арифметики вычетов, которую часто еще называют модульной арифметикой или модулярной арифметикой. Если это так, то искомое уравнение мы можем записать в виде очень простого уравнения (2).
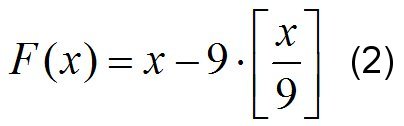
Это же уравнение можно записать в общем виде путем замены числа 9 на модуль m (для целей нумерологии наиболее часто имеет значение – 9), который теоретически может быть равен любому натуральному числу:
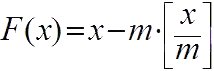
Формула выполняет процедуру замены исходного числа его остатком от целочисленного деления на модуль m. Необходимо отметить, что в арифметике вычетов эту процедуру по непонятным причинам предпочитают задавать не в виде формулы, а словесными формулировками. Возможно, использование формулы позволило бы лучше понять суть применения арифметики вычетов и избежать появления многих ошибочных утверждений.
Однако радоваться тому, что математики подарили нумерологам простую и удобную формулу нумерологического сокращения чисел все же не стоит. Сначала проведем экспериментальную проверку этого математического утверждения. Кстати проведение экспериментальной проверки является одним из критериев лженаучности. Следовательно, мы сразу проверим это математическое утверждение и на лженаучность.
И так возьмем число 17 и сократим его обычным, принятым в современной нумерологии методом, т. е. сложим цифры 1 и 7. В результате получим 8. Теперь разделим 17 на 9 и мы увидим, что остатком от этого целочисленного деления будет тоже число 8. Получается, что рассматриваемое нами математическое утверждение вроде бы верно, но не будем торопиться, а проведем еще один эксперимент.
Теперь возьмем число 18. 1+8=9, т. е. нумерологически число 18 сокращается до 9. Теперь 18/9=2, т. е. 18 делится на 9 без остатка или остаток от этого деления равен 0, а вовсе не 9, как это должно быть согласно, рассматриваемого нами математического утверждения.
Для всех чисел кратных 9 (или кратных выбранному другому значению m), рассматриваемое математическое утверждение будет ошибочным. Таким образом, это математическое утверждение должно быть отнесено к лженаучным. Но в научном сообществе его лженаучным никто не назовет, а в лучшем случае назовут его ошибочным, в худшем – вообще комментировать, и обсуждать не будут. Именно этот подход является основной причиной отсутствия четких и формальных критериев для разделения лженауки и науки. В результате это разделение происходит не объективно, а субъективно, что в будущем позволяет до бесконечности подвергать сомнению результаты такого разделения.
Вообще в математике встречаются очень часто ошибочные утверждения, парадоксы и всякого рода заблуждения. Про некоторые из них я уже писал: Многогранник – единая и универсальная геометрическая форма всего http://stob2.narod.ru/10i.htm ; Неудобные вопросы и парадоксы современной топологии http://stob2.narod.ru/33s.htm ; Великая теорема ферма не верна имеются ее решения среди бесконечных целых чисел Теоретически доказать ее не возможно Математика Теория чисел http://stob2.narod.ru/14s.htm ; Элементарная односторонняя поверхность не является листом Мебиуса http://stob2.narod.ru/32s.htm .
Само утверждение о том, что математика это точная наука вообще-то тоже является распространенным и очень старым заблуждением. Говорить о том, что математика является точной наукой можно лишь в отношении отдельных ее разделов.
Несмотря на то, что, как уравнение (2), так и математическое утверждение на основании, которого оно было составлено, оказались ошибочными, их все же можно использовать для получения уравнения нумерологического сокращения чисел. Очевидно, что для этого уравнение (2) просто необходимо дополнить выражениями, позволяющими в ходе выполнения вычислений 0 заменять на 9. В результате можно получить вариант уравнения (3) нумерологического сокращения чисел.
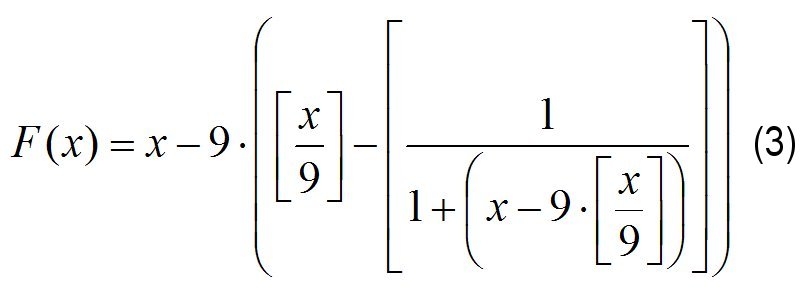
Это же уравнение можно записать в общем виде путем замены числа 9 на модуль m (для целей нумерологии наиболее часто имеет значение – 9), который теоретически может быть равен любому натуральному числу:
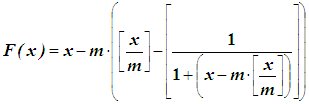
При помощи уравнения (3) теоретически можно осуществлять нумерологическое сокращение любых чисел от 1 до бесконечности. При этом в ходе применения уравнения (3) не требуется использовать дополнительные словесные пояснения. Число сокращается в ходе непрерывных вычислений по уравнению (3).
На основе уравнения (3) на JavaScript был создан, приведенный в этой статье, очень простой калькулятор нумерологического сокращения чисел:
Этот калькулятор, конечно, не может производить сокращения очень больших чисел, так как любой компьютер имеет известные ограничения своих возможностей. Однако для практического применения он вполне подходит, ведь человеку, как правило, не приходиться иметь дело с очень уж большими числами.
Кроме калькулятора на JavaScript была написана программа, обеспечивающая получение калькулятора нумерологического сокращения чисел в более привычном для калькуляторов виде и способная работать без браузера и загрузки данной статьи, которую можно загрузить по ссылке:
Уравнение (3) задает функцию изменения значений нумерологического сокращения числа по мере изменения величины этого числа. Очевидно, что чем сложнее будет эта функциональная зависимость, тем теоретически более подробный и точный нумерологический прогноз можно получить. На Рис. 1 показан график функции нумерологического сокращения чисел, построенный при помощи уравнения (3).

Рис. 1 Функция нумерологического сокращения чисел до цифр от 1 до 9
Как видно из графика на Рис. 1 функция нумерологического сокращения чисел до цифр от 1 до 9 вовсе не является сложной и представляет собой импульсную периодическую функцию. Такие функции известны уже сравнительно давно. О методах их задания можно посмотреть в статье: Периодические импульсные функции на основе универсального уравнения http://stob2.narod.ru/16s.htm .
Однако в нумерологии иногда используются не только цифры, но и числа с большим количеством знаков. В некоторых вариантах нумерологических расчётов двузначные числа 11 и 22, также называются господствующими, и не сокращаются до однозначных. Известна, так называемая, русская школа нумерологии, которая отличается от всех остальных нумерологических школ тем, что в ней определены прямые характеристики свыше 150 чисел. Поэтому здесь на Рис. 2 приведен график функции нумерологического сокращения чисел до двухзначного числа.

Рис. 2 Функция нумерологического сокращения чисел до двухзначного числа
График функции нумерологического сокращения чисел до двухзначного числа был построен при помощи уравнения (3) путем подстановки в него значения m = 99.
График на Рис. 2 выглядит более сложным, чем график на Рис. 1, но, тем не менее, если исходить из его вида, то все же не следует рассчитывать на очень подробные и одновременно точные нумерологические прогнозы и на основе чисел, сокращенных до уровня двухзначных чисел.
Поэтому представляется, что составление качественных нумерологических прогнозов должно осуществляться на основе учета сразу нескольких влияющих факторов, каждый из которых можно выразить своим числом. Конечно, составление таких нумерологических прогнозов является совсем непростым делом и требует привлечения к их составлению высококвалифицированных нумерологов. Полностью формализовать же процедуру составления многофакторных нумерологических прогнозов в ближайшее время вряд ли удастся.
Сильная зависимость от искусства нумеролога позволит продолжить свою критику нумерологии борцам с лженаукой, но не следует забывать то, что еще вчера выглядело логично, обоснованно и незыблемо уже завтра будет выглядеть совсем не так. Все в нашем мире развивается и изменяется, постоянно обнаруживаются новые ошибки и неточности. О чем, очень хорошо свидетельствуют, приведенные в данной статье примеры и ссылки на примеры из других статей.
Сказанное здесь может породить неверное представление о простоте процедуры составления нумерологических прогнозов, а, следовательно, и проверки их состоятельности. Действительно – присвоил изменениям влияющих факторов числовые значения, собрал статистику, как эти изменения влияют на объект прогнозирования, затем так или иначе объединил статистическую информацию по этим факторам и получил нумерологический прогноз, но, к сожалению, этого будет недостаточно. Таким образом, на радость борцам с лженаукой, чаще всего в лучшем случае можно получить очень общий и расплывчатый прогноз.
Дело в том, что формула (3) задает периодическую импульсную функцию и позволяет преобразовывать ряд натуральных чисел в бесконечно повторяющуюся последовательность чисел следующего вида: 1, 2, …, m, 1, 2, …, m, …. То есть данная периодическая функция в пределах каждого своего периода последовательно принимает значения от 1 до m. При этом, как и в случае классического нумерологического сокращения чисел, появление в получающейся последовательности чисел нуля практически невозможно.
Тут необходимо отвлечься и четко пояснить, почему использование нуля в нумерологии является неприемлемым.
Нумеролог работает с реальными событиями и объектами, на формирование и развитие которых, всегда требуется определенное время, и их свойства всегда характеризуются вполне конкретным набором чисел. И эти числа не могут быть нулевыми, так как, например, невозможно за нулевое время родить ребенка, построить здание или корабль, а если у человека есть имя, место рождения, то их свойства не могут быть нулевыми. Если событие или объект имеют нулевые характеристики, то это означает, что они в реальности не существуют.
Кроме этого есть и чисто математическая проблема в использовании нуля. Нумеролог, с другой стороны, работает так же и с числами, характеризующими свойства событий или объектов, а ноль, несмотря на всеобщее признание в настоящее время его числом, вообще то числом не является. И, как это не удивительно, но никаких доказательств, обоснований того, что ноль является числом, не существует.
В настоящее время ноль относят к множеству целых чисел, которое рассматривается как расширение множества натуральных чисел, получаемое добавлением к нему отрицательных чисел, не являющихся дробями, и нуля. Хотя такое представление множества целых чисел будет не совсем корректным в связи с тем, что в части стран ноль считают не только целым числом, но еще и натуральным числом. Да, до сих пор не удалось получить четкого обоснования того, является ли ноль натуральным числом или нет. Это обстоятельство свидетельствует в пользу того, что с нулем, при рассмотрении его в качестве числа, не все в порядке и его свойства отличаются от свойств остальных чисел. Ведь для всех чисел кроме нуля подобного раздвоения мнений не возникает.
Множество определяют как набор, совокупность или собрание каких-либо объектов, которые обладают общим для всех них характеристическим свойством и называют элементами этого множества.
Множество целых чисел бесконечно и по этому задать его можно только методом описания, то есть, задавая условие, которому удовлетворяют все элементы, принадлежащие этому множеству и которому не удовлетворяют элементы, ему не принадлежащие.
Удовлетворяет или нет, заданному условию, кандидат в элементы множества определяется его свойствами и именно по этому желательно, чтобы свойства нуля не отличались от свойств остальных чисел множества целых чисел. Но, как известно, их свойства весьма сильно отличаются друг от друга. Однако отличие свойств может не повлиять на включение нового элемента во множество, если эти отличия не затрагивают, так называемое, характеристическое свойство. Для проверки этого обстоятельства достаточно вычислить отношение между значениями характеристических свойств элементов множества и если это отношение будет выражаться в виде конкретного числа, то проверяемые элементы будут принадлежать одному множеству, а если нет, то не будут.
Например, рассмотрим множество выпуклых многоугольников.
В общем случае многоугольник определяют как плоскую замкнутую ломаную линию. Выпуклый многоугольник это многоугольник, который лежит по одну сторону от любой прямой, содержащей его сторону, то есть продолжения сторон многоугольника не пересекают других его сторон. Вершины ломаной линии, образующей многоугольник, называются вершинами многоугольника, а её звенья — сторонами многоугольника.
Ясно, что построить замкнутую ломанную линию меньше чем из трех звеньев невозможно и поэтому рассматриваемое множество будет начинаться с треугольника и далее включать в себя четырехугольник, пятиугольник, шестиугольник и так далее до бесконечности. При этом в качестве характеристического свойства элементов данного множества можно рассматривать наличие трех и более вершин или сторон.
Теперь вычислим отношение между значениями характеристических свойств элементов множества выпуклых многоугольников. Для треугольника и четырехугольника это отношение будет выражаться числом 4/3. Для четырехугольника и пятиугольника это отношение будет выражаться числом 5/4. Для пятиугольника и шестиугольника это отношение будет выражаться числом 6/5. Очевидно, что и дальше, до бесконечности отношение будет выражаться конкретным числом. А это означает, что все рассматриваемые фигуры можно отнести к множеству многоугольников.
А теперь предположим, что отрезок тоже является элементом множества многоугольников. Значение характеристического свойства множества многоугольников у отрезка будет равно нулю, так как у отрезка отсутствуют вершины и соответственно стороны. Тогда отношение значений характеристических свойств отрезка и треугольника будет выглядеть как выражение 3/0, которое не является числом, так как ничего делить на ноль нельзя, и выполнение такой операции лишено смысла. Этого достаточно для того, чтобы утверждать, что отрезок никак не может являться элементом множества многоугольников.
Точно по таким же основаниям точка не являться элементом множества многоугольников.
Рассмотренная процедура универсальна и подходит для анализа элементов любого множества. Поэтому проверим при помощи нее элементы множества целых чисел.
В качестве характеристического свойства элементов множества целых чисел можно рассматривать возможность представления любого из них в виде суммы положительных и отрицательных единиц при условии, что общее количество единиц в сумме будет выражаться натуральным числом. Можно легко убедиться, что это условие выполняется для любого элемента множества целых чисел. Действительно –4=-1+-1+-1+-1, 0=-1+1, 1=-1+1+1, 5=1+1+1+1+1 и подобные суммы можно составить для любого целого числа. При этом еще и вариантов таких сумм для каждого целого числа можно получить бесконечно много. Например, 3=1+1+1, 3=1+1+1+1+-1, 3=1+1+1+1+1+-1+-1, … А вот представить любое нецелое число в виде суммы единиц невозможно. Например, число 5,5 так представить, никак не удастся.
Необходимо отметить, что рассматриваемое здесь характеристическое свойство элементов множества целых чисел не совсем корректно из-за того, что оно специально было составлено так, чтобы ему удовлетворял ноль. Если его немного изменить, то можно получить полностью корректное характеристическое свойство.
Теперь вычислим отношение между значениями характеристических свойств элементов множества целых чисел. Для 1 и 2 это отношение будет выражаться числом 2/1. Для 2 и 3 это отношение будет выражаться числом 3/2. Для 3 и 4 это отношение будет выражаться числом 4/3. Очевидно, что и дальше, до бесконечности отношение будет выражаться конкретным числом. А это означает, что все рассматриваемые числа можно отнести к множеству целых чисел. Точно такие же результаты будут получаться и с использованием отрицательных чисел. И лишь для 0 и, например, 1 это отношение будет выражаться как 1/0. Выражение 1/0 не является числом, так как ничего делить на ноль нельзя, и выполнение такой операции лишено смысла. Этого достаточно для того, чтобы утверждать, что ноль никак не может являться элементом множества целых чисел и вообще числом не является.
Конечно, можно заявить, что уже около трех веков, как ноль окончательно стали считать числом и никаких критических проблем с этим связанных вроде не наблюдается. На самом деле проблемы есть и об их существовании свидетельствует целый список особых свойств и правил выполнения операций с нулем, некоторые из которых, даже вынуждены были принять по соглашению. Можете себе представить, например, что значение дважды два мы не вычислили, а приняли по некоему соглашению? А вот для того, что бы ноль признать числом на подобное пришлось пойти.
Отсутствие же критических проблем, приводящих к неустранимым противоречиям, при использовании нуля в качестве числа связано с тем, что ноль и все числа являются абстрактными объектами, среди них нет реальных или конкретных объектов, наличие которых могло бы вызвать неустранимые противоречия.
Я специально привел пример с множеством многоугольников и геометрической точкой. Точку можно рассматривать, в определенном смысле, в качестве некоего подобия нуля. Геометрическая точка является абстрактным объектом, а вот каждый из многоугольников, как и объекты, рассматриваемые нумерологами, являются конкретными объектами и именно поэтому точку не стали наделять особыми свойствами и включать в какое-либо конкретное множество геометрических фигур.
Что еще нужно сказать о проблеме использования нуля в нумерологии? Это то, что если бы действительно связь чисел с объектами, процессами, жизнью людей и т. п. была бы лишь мистической, как утверждают борцы с лженаукой, то признание нуля в качестве числа не должно бы было никоим образом отразиться на прогнозах нумерологии и более того, его бы без проблем стали бы использовать при нумерологическом прогнозировании.
Однако борцы с лженаукой этот вопрос исследовать не захотели и вообще о проблеме нуля предпочли не упоминать. Есть основания полагать, что так они поступили вовсе не по незнанию или недомыслию, а умышленно. Об основаниях полагать, что нумерология была очернена злонамеренно, будет еще сказано далее.
В этой связи очень кстати пришлись приведенные некоторыми нумерологами значения числа ноль. Хотя процедура классического нумерологического сокращения чисел исключает возможность их использования. Борцы с лженаукой вообще предпочли оценить нумерологические прогнозы отдельных нумерологов, а не исследовать методы нумерологии. А затем отрицательные результаты отдельных нумерологов распространить на всю нумерологию. В связи с этим возникает вопрос, зачем им потребовалось поступать таким странным образом? Это только внешне подобные исследования выглядят научно обоснованными, а фактически они порочны и даже абсурдны. Например, известно, что учеными-физиками было высказано немало утверждений, которые в последствии были признаны ошибочными. Так вот, представьте себе, что кто-то выбирает случайным образом с десяток таких высказываний и заявляет, что поскольку утверждения отдельных физиков при их проверке дали отрицательный результат, то вся физика и ее методы являются лженаучными. В общем, получается полный абсурд. Но вот в отношении нумерологии подобный абсурд почему-то считается вполне допустимым. В связи с этим становится, еще более интересен, высказанный выше вопрос, зачем это делают борцы с лженаукой?
Необходимо так же отметить, что именно борцы с лженаукой утверждают, что в нумерологии рассматриваются только мистические связи чисел с физическими объектами, процессами и тому подобным. Конечно, глупо утверждать, что реально существующие объекты не имеют никаких связей с числами. Ведь свойства любого объекта количественно выражаются через числа. Например, изготовили десяти килограммовую гирю. Эта гиря будет связана с числом десять, так как одно из ее свойств количественно выражается именно через это число. Вот только совершенно не понятно в чем борцы с лженаукой усмотрели мистику в подобной связи?
В том, что ноль в нумерологии не связан с реально существующими объектами и процессами тоже никакой мистики нет, просто ноль не является числом. И если и существует в связи с нулем какая-то мистика, то выражается она в том, что математики согласились считать ноль числом. Иначе как мистикой это и не объяснишь.
Такое большое отступление пришлось сделать для того, чтобы наиболее полно объяснить, почему формула (3) никогда не возвращает ноль и это действительно важный момент. Теперь можно вернуться к анализу формулы (3).
Например, ряд натуральных чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, … при помощи формулы (3) преобразуется в бесконечно повторяющуюся последовательность чисел следующего вида для значения m = 5 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, …, для значения m = 9 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, 7, 8, 9, …, для значения m = 12 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 1, 2, 3, 4, 5, 6, … Эти примеры показывают, что период функции заданный формулой (3) определяется значением модуля m. С другой стороны из формулы (3) так же следует, что любой процесс развития любого объекта во времени будет периодическим или повторяющимся.
Вообще то нумерологи и без формулы (3) еще с глубокой древности придерживались точки зрения, что время движется по нескончаемо повторяющимся циклам от 1 до 9. Периодичность или цикличность различных процессов в живой и неживой природе, в истории, в экономике и т. д. отмечали не только нумерологи. О различных выявленных циклах примерно за последние 150 лет сообщалось в очень большом количестве публикаций. Основной претензией к подобного рода исследованиям является то, что выявленные циклы и периодические процессы обычно носят нерегулярный характер. Если, конечно, не учитывать такие процессы как движение космических тел вокруг центра Галактики, движение планет вокруг Солнца, колебание векторов магнитной индукции и электрической напряжённости в электромагнитной волне, распределение электронной плотности вокруг ядра атома и др. подобные процессы со стабильными периодами. Однако нумерологи, как правило, периодические процессы со стабильными периодами не изучают.
С другой стороны идеальных периодических процессов в природе существовать не может. Даже те процессы, которые принято относить к процессам со стабильными периодами все же таковыми не являются по причине того, что ничего неизменного вокруг нас нет. Например, электромагнитная волна, в какой то момент может столкнуться с препятствием и быть полностью поглощена, планета столкнуться с другим массивным телом, что приведет к значительным изменениям параметров ее обращения вокруг звезды.
Рассчитывать на идеальный периодический процесс можно только в том случае, если поведение изучаемого объекта описывалось бы при помощи одного единственного уравнения (3). Но, как уже говорилось выше, поведение любого реального объекта может быть описано только суммой очень большого количества уравнений вида (3) да еще и с очень разнообразными по величине значениями модулей m.
Почему значения модулей m должны быть обязательно разнообразны? Потому что, элементарно, бывают процессы, протекающие быстро, бывают медленные, а бывают очень медленные. Это, конечно, по восприятию человека.
Например, извержения Йеллоустонского супервулкана происходят примерно каждые 600 000 лет. Примерно потому что само извержение в свою очередь происходит под воздействием громадного количества только сильно влияющих на него факторов, которые то же не стабильны во времени, не говоря еще и о слабо влияющих факторах. Поэтому для наблюдателя подобные процессы выглядят как нерегулярные.
Так вот, для таких очень медленных процессов значения или характеристики вычисленных по формуле (3) нумерологических чисел будут оставаться практически неизменными за исключением момента катастрофы (в данном случае извержения) и сразу после нее (периода восстановления). То есть большую часть времени влияние вулкана можно не учитывать без заметной потери точности прогнозов. Но если, например, не учесть влияние вулкана на прогноз успешности предприятия в момент извержения или сразу после него, то такой прогноз точно не сбудется, так как предприятие просто перестанет существовать.
В качестве критики, высказанного здесь, можно услышать, что вокруг нас наблюдается много разовых явлений, которые никак не могут быть периодическими процессами. Но разовыми они могут нам только казаться, так как выходят за пределы возможностей наших наблюдений и, кроме того, для таких явлений просто можно выбрать очень большие значения модулей m, в пределе бесконечно большие и формулу (3) можно будет продолжать использовать. Например, Большой взрыв произошел для человека запредельно давно, но он продолжает оказывать влияние буквально на все процессы и, кроме того, позволяет объяснить, почему во Вселенной всё оказалось связано со всем, не смотря на гигантские размеры Вселенной. Просто всё провзаимодействовало еще в момент Большого взрыва, когда Вселенная была очень маленькой. Когда же ученые говорят о том, что во Вселенной существуют предельные расстояния, определяемые скоростью света, на которых может быть оказано воздействие, то они говорят это без учета взаимодействий в прошлом. О том почему, они так поступают, будет сказано далее.
Таким образом, все, что мы видим вокруг, возникло, сформировалось и т. д. из-за взаимодействия всего со всем и ничего случайного быть не может. А значит, теоретически, всегда можно составить точный прогноз дальнейшего развития любого процесса, в том числе и методами нумерологии. Причем по ряду причин такой прогноз в первую очередь можно получить именно методами нумерологии. То, что ничего случайного быть не может, выражается и в числах. Так математики не смогли создать арифметический генератор случайных чисел, более того в настоящее время они пришли к выводу, что такой генератор невозможен. И вынуждены были использовать так называемый генератор псевдослучайных чисел представляющий собой алгоритм, порождающий последовательность чисел, элементы которой лишь почти независимы друг от друга, и подчиняются заданному распределению. То есть, человек оказался не в состоянии предложить даже математическую модель получения случайных событий.
Правда считается, что истинные случайные числа можно получить при помощи, так называемых, физических источников случайных чисел. В качестве таких источников обычно предлагаются детекторы событий ионизирующей радиации, дробовой шум в резисторе, космическое излучение или более простые и доступные: шум звуковой карты, счётчик тактов процессора и тому подобное. Вот только не существует никаких доказательств случайности получаемых на подобных устройствах результатов. То, что в настоящее время не удается предсказать результаты работы устройств на основе таких источников, вовсе не является доказательством, так как это вполне может означать, что мы просто пока не научились этого делать.
И, конечно же, данная проблема представителями официальной науки рассматривается исключительно в качестве частной проблемы математиков и разработчиков компьютерной техники. В связи, с чем борцам с лженаукой можно было даже не упоминать о возможной связи этой проблемы и методов нумерологии.
То, что наблюдаемые процессы, события выглядят, как нерегулярные вовсе не приводит к невозможности использования на практике методов нумерологии. В физике уже давно находят законы движения тела, участвующего одновременно в нескольких колебательных процессах путем сложения колебаний. И то, что результат такого сложения внешне часто выглядит, именно, как нерегулярные колебания не препятствует точному расчету положения тела в пространстве в любой момент времени.
По этому в начале статьи, по аналогии, и говорилось о том, что для повышения точности прогнозов необходимо учитывать влияние как можно большего количества факторов.
Технически это будет означать, что для каждого фактора нужно будет определять свое значение модуля m и по формуле (3) вычислять нумерологически сокращенные числа, для которых уже определять их значения. Причем для каждого фактора значения нумерологически сокращенных чисел будут уникальны и более того сразу несколько нумерологически сокращенных чисел могут иметь одинаковые или очень близкие значения. Особенно это будет характерно для больших значений модуля m. При этом речь будет идти об учете не трех – пяти факторах, а о тысячах.
Конечно, такое прогнозирование потребует выполнения очень большого объема вычислений с одновременной обработкой значительных по объему баз данных, в которых в первую очередь будет находиться информация о значениях нумерологически сокращенных чисел для каждого из факторов. А ведь эти базы нужно еще создать.
По этому в глубокой древности, когда нумерология только зарождалась, пришлось довольствоваться учетом одного фактора и одним значением модуля m=9. По сути, благодаря развитию вычислительной техники, мы совсем недавно только подошли к возможности получения относительно точных нумерологических прогнозов.
И так как сами практикующие нумерологи ничего этого не использовали, то, и борцы с лженаукой тем более утруждать себя анализом теоретических основ нумерологии не стали и ограничились оценкой работы, согласившихся участвовать в их экспериментах, нумерологов. Вообще-то особых претензий к борцам с лженаукой не было бы, если бы они ограничились бы критикой участников экспериментов, но они распространили отрицательные результаты работы отдельных нумерологов на все методы нумерологии. Это все равно, что найти расчет моста с ошибками, построить в соответствии с ним мост, убедиться, что мост разрушился и на этом основании заявить, что все методы расчета мостов являются лженаучными. И опять трудно поверить в то, что борцы с лженаукой не знали или не понимали, что так делать нельзя.
Одним из важных вопросов является возможность, используя методы нумерологии, получать всегда точные прогнозы. Получение абсолютно точных нумерологических прогнозов возможно лишь теоретически. Практически же этого сделать невозможно из-за того, что влияющих факторов просто запредельно много, возможно, даже бесконечно много, а это значит, что для получения абсолютно точного прогноза пришлось бы просчитать бесконечно много формул (3). С этим не справится никакая существующая вычислительная техника, и создать в будущем, способную за разумное время производить такие объемы вычислений технику, невозможно. В связи с этим абсолютная воспроизводимость результатов в нумерологии не достижима.
Прочитав о невозможности достижения абсолютного воспроизведения результатов методами нумерологии, непорядочные борцы с лженаукой обрадуются и скажут: вот по этому мы и говорим, что нумерология это лженаука. Ведь истинно научные методы дают стопроцентное воспроизведение своих результатов.
Действительно, ученые в совершенно разных областях науки и техники делают расчеты, а затем неизменно экспериментально подтверждают результаты этих расчетов. И на этом фоне, возможно, не всем понятно, почему я борцов с лженаукой назвал непорядочными людьми? В чем состоит их непорядочность? Так вот, поясняю, и рассказываю, в чем состоит их главный обман, о котором борцы с лженаукой, ясное дело, предпочитают не рассказывать.
Дело в том, что все существующие математические модели являются идеализированными. Это означает, что на их адекватность можно рассчитывать только в строго определенных условиях (соблюдении ограничений), которые заранее были предусмотрены в математической модели. И когда проводят экспериментальную проверку результатов расчета, то строго следят, чтобы условия проведения эксперимента не выходили за пределы условий (ограничений) математической модели. То есть, если на объект экспериментальной проверки в ходе проведения эксперимента, повлияют какие либо факторы, которые не были учтены в математической модели, то расчетный результат не совпадет с результатом эксперимента и соответственно экспериментальное подтверждение не состоится. Согласитесь, это как-то не похоже на абсолютное или стопроцентное воспроизведение результатов истинно научных методов, о которых нам говорят борцы с лженаукой. И в реальности прогнозы, сделанные, так называемыми, научными методами очень часто не подтверждаются. Примеров этому просто огромное количество.
Вот все конструкции самолетов в настоящее время рассчитываются по научно обоснованным методикам. В результате получают прогноз характеристик самолета еще до его постройки, таких как дальность и скорость полета, вес, длина разбега и так далее. И конечно фактически делают главный прогноз, что самолет будет летать и при этом не падать или не разрушаться. Однако на практике мы наблюдаем довольно многочисленные происшествия с самолетами.Даже если происшествие с самолетом повлекло за собой тяжелые последствия, никто не будет заявлять о том, что научно обоснованные методы расчета самолета не подтвердили свою состоятельность на практике. Ведь тогда разработчики методов расчета самолета перестанут отличаться от нумерологов, и их придется объявлять лжеучеными. По этому после расследования происшествия будет объявлена его причина. Обычно это бывает ошибки пилотирования, отказ техники, террористический акт, алкогольное опьянение или психическое состояние членов экипажа и тому подобное, то есть именно те факторы, которые оказывают существенное, но не регулярное влияние и не учитываются в математической модели самолета. Те же факторы, которые вызывают лишь незначительные отклонения от расчетных параметров полета самолета вообще мало кого интересуют. Да и учесть их в методиках расчета физически невозможно из-за очень большого их количества. По этому небольшие отклонения результатов эксперимента от результатов расчета считаются вполне приемлемыми и в случае наличия таких отклонений теории обычно не ставятся под сомнения.
Например, если кто-то думает, что движение небесных тел (звезд, планет, комет, астероидов, галактик в целом,…) точно совпадает с расчетным, то он глубоко ошибается. В реальности всегда наблюдаются отклонения. Просто, если отклонения небольшие, то на них не обращают внимание. Если отклонения существенны и наблюдаются локально для одного или небольшой группы объектов, то ищут влияние не учтенного ранее объекта (звезды, планеты,…), то есть аналога пьяного пилота или террориста. Если же отклонения существенны и носят всеобщий характер, то начинают искать темную материю и энергию.
Приведенные примеры показывают, что не всегда возможно проведение эксперимента с идеализированными объектами в идеализированном пространстве. Если в случае испытания самолета можно подготовить идеализированный объект - самолет, изготовив его из тщательно отобранных деталей, залив в него проверенный керосин, усадив в него соответствующий экипаж и так далее по списку, и идеализированное пространство тоже можно получить, просто дождавшись нужных погодных условий, то в случае с небесными телами этого сделать невозможно. Действительно человек не может изменить свойства звезд или планет, не может он хоть как-то повлиять и на пространство окружающее эти звезды и планеты. В данном случае остается только осуществлять наблюдения.
В связи с этим в ходе экспериментальных проверок допускались незначительные отклонения от результатов расчетов, а если отклонения были значительными, то допускались корректировки математических моделей в частности за счет учета в них дополнительных факторов.
Вообще, то, что экспериментальную проверку могут пройти только идеализированные объекты нормально. Ведь абсолютное или стопроцентное воспроизведение в эксперименте результатов любых расчетов невозможно. Не нормальным является то, что борцы с лженаукой обманывают, выдавая экспериментальную проверку идеализированных объектов за экспериментальную проверку неидеализированных реальных объектов. И на этом основании требуют от нумерологических прогнозов абсолютного стопроцентного их воспроизведения не в условиях идеализированного пространства, а реального пространства. И уж тем более не допускают даже саму возможность корректировки математических моделей для составления нумерологических прогнозов за счет учета дополнительных факторов. Таким образом, предъявляя к методам нумерологии намного более жесткие требования, чем к методам, так называемого, истинно научного прогнозирования.
Причем есть основания полагать, что борцы с лженаукой намеренно создают иллюзию несостоятельности методов нумерологии, так как они просто не могут не знать, как проводятся научные исследования и как разрабатываются математические модели. Ведь все они прошли соответствующее обучение.
Вообще когда начинаются исследования не идеализированных, а реальных объектов, то, как положительный, так и отрицательный результат ничего не говорит о состоятельности методов исследования. Он лишь подтверждает или опровергает некую гипотезу.
Например, археологи предположили, что в некотором месте в древности располагалась стоянка человека. Они произвели раскопки и ничего не нашли, что опровергает гипотезу о наличии стоянки древнего человека в данном месте, но очевидно не доказывает несостоятельность методов археологии и тем более не может служить доказательством лженаучности археологии.
По этому никакие эксперименты с идеализированными или неидеализированными объектами не могут послужить основанием для объявления лженаучными любых научных методов, в том числе и нумерологических. И об этом точно знают борцы с лженаукой просто в силу своей квалификации. Вообще даже и без всякой квалификации понятно, что искать связи можно чего угодно с чем угодно, и ничего лженаучного в самом этом процессе нет. И результат этих поисков тоже может быть любым. Главное чтобы этот результат умышленно не искажался.
Существует и формальный, очень простой, критерий, позволяющий отделить лженауку от науки это умышленное искажение или подделка результатов исследований. Вот только борцы с лженаукой предпочитают его игнорировать и понятно почему. Дело в том, что их работодатели, особенно часто в экономике, требуют обосновать, так называемые, непопулярные реформы. А сделать этого без умышленного искажения результатов исследований невозможно. Вот чтобы ученых занимающихся такими обоснованиями не объявлять лжеучеными, лучше вообще о таких критериях даже не упоминать.
Кроме этого необходимо отметить, что вся эта возня с борьбой с лженаукой не так уж безобидна и не обходится без последствий. В результате нумерология лишена возможности нормально развиваться, использовать ту же вычислительную технику достаточной мощности. Между тем методы нумерологии в отличие от других существующих в наше время научных методов позволяют при прогнозировании одновременно учитывать влияние самых разнообразных факторов. Например, это позволит получить прогноз возникновения нештатной ситуации с конкретным самолетом и с учетом таких факторов, как совершение тер акта, появления нетрезвого пилота, резкое ухудшение погодных условий и тому подобных.
Если бы люди знали, что по нумерологическому прогнозу с конкретным самолетом с вероятностью 10-20 процентов произойдет нештатная ситуация, то они хотя бы могли сами решать стоит им лететь этим самолетом или нет. Но их фактически лишили такой возможности.
январь 2013 года