
Рис. 1 пример листа Мебиуса
| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |
Самой известной односторонней (неориентируемой) поверхностью с краем является лист Мебиуса (или лента Мебиуса, петля Мебиуса, Mobius strip ) (Рис. 1).

Рис. 1 пример листа Мебиуса
Кроме односторонних поверхностей с краем существуют и односторонние поверхности без края или, как их еще называют, замкнутые (наиболее известны – бутылка Кляйна и проективная плоскость). Однако все они существуют лишь в четырехмерном пространстве, так как в трехмерном пространстве без самопересечения построить их не удается. Несомненно, лидером по известности является односторонняя поверхность - бутылка Кляйна (Рис. 2). На рисунке хорошо видно, что она самопересекается, а вот представить, как бутылка Кляйна выглядит в четырехмерном пространстве затруднительно.

Рис. 2 пример бутылки Кляйна в трехмерном пространстве
Почему в трехмерном пространстве не удается получить модель односторонней поверхности без края? Ведь, например, бутылка Кляйна делается на основе двух листов Мебиуса. А лист Мебиуса считается элементарной односторонней поверхностью с краем, т. е. самой простой, из всех возможных, моделью такой поверхности. И если даже на основе модели самой простой односторонней поверхностью с краем в трехмерном пространстве не удается получить модель односторонней поверхности без края, то означает ли, что это действительно невозможно?
Нет, не значит. Дело в том, что на самом деле лист Мебиуса вовсе не является самой простой моделью односторонней поверхности с краем. Об этом было подробно написано в статье: "Элементарная односторонняя поверхность не является листом Мебиуса" (http://stob2.narod.ru/32s.htm). В этой же статье была предложена более простая, чем лист Мебиуса модель односторонней поверхности с краем (Рис. 3).

Рис. 3 пример простейшей модели односторонней поверхности с краем
Если сравнить фигуры изображенные на Рис. 1 и Рис. 3, то станет очевидным, что главное их отличие друг от друга состоит в том, что фигура на Рис. 3 изготовлена просто из полоски, а лист Мебиуса из полоски, закрученной относительно ее продольной оси на пол-оборота или фактически лист Мебиуса изготовлен из геликоида. Именно "закрученность" полоски в геликоид при изготовлении листа Мебиуса и делает в трехмерном пространстве невозможным полностью замкнуть край листа Мебиуса. Этой проблемы с фигурой, изображенной на Рис. 3 не возникает.
На Рис. 4 приведена схема фигуры с Рис. 3. На схеме (Рис. 4) стрелками показаны направления замыкания края.
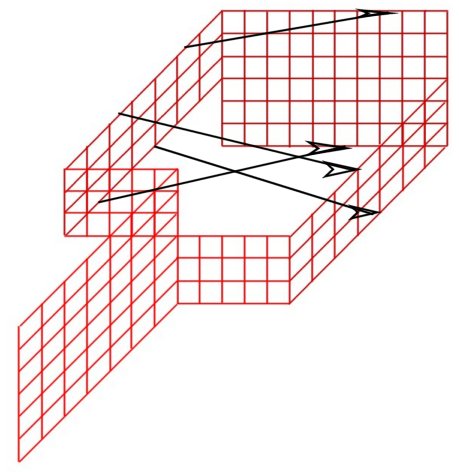
Рис. 4 схема простейшей модели односторонней поверхности с краем
По мере замыкания края его общая длина сокращается, а фигура (Рис. 3) трансформируется в фигуру "сумка" (Рис. 5 – представлена в виде материальной модели), которая подробно была описана в статье: "Элементарная односторонняя поверхность не является листом Мебиуса" (http://stob2.narod.ru/32s.htm).

Рис. 5 материальная модель односторонней поверхности с краем - сумка
Для полного замыкания края фигуры (Рис.3) к ее поверхности присоединяется дополнительная поверхность, которая на схеме (Рис. 6) показана зеленым цветом.
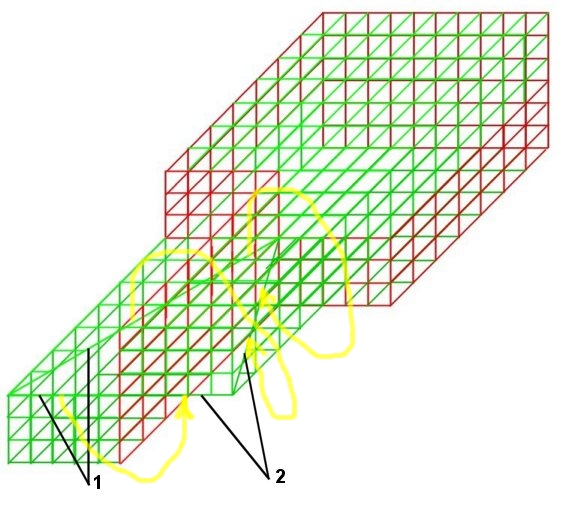
Рис. 6 схема полного замыкания края простейшей модели односторонней поверхности с краем
Однако в результате получаются два новых края, обозначенные на Рис. 6 цифрами 1 и 2, которые в свою очередь можно замкнуть, продлевая поверхность по направлению желтых стрелок.
На Рис. 7 показана материальная модель поверхности соответствующая схеме показанной на Рис. 6.

Рис. 7 материальная модель поверхности соответствующая схеме показанной на Рис. 6
На Рис. 8 представлена схема односторонней поверхности без края, где синим цветом выделена часть поверхности, достроенная по направлению желтых стрелок и замыкающая края 1 и 2 показанные на Рис. 6. При этом край 1 и отверстие возле него окажутся полностью закрытыми.
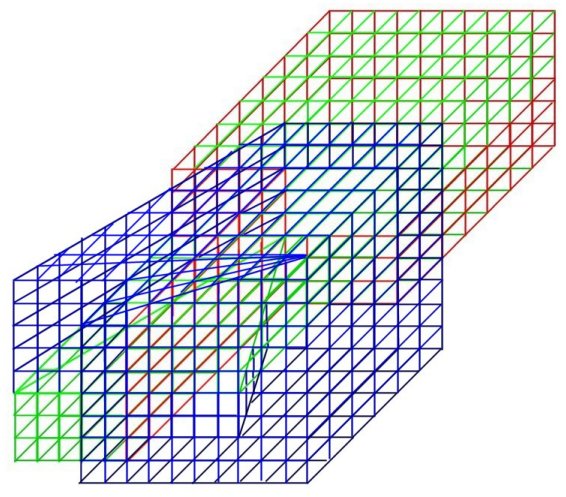
Рис. 8 схема односторонней поверхности без края
На Рис. 9 представлена материальная модель односторонней поверхности без края соответствующая схеме на Рис. 8.

Рис. 9 материальная модель односторонней поверхности без края соответствующая схеме на Рис. 8
Для того чтобы в устройстве модели односторонней поверхности без края (Рис. 9) было проще разобраться, в нее были помещены орехи. В результате стало возможно понять, что у этой поверхности действительно отсутствует край. Если по этой поверхности заставить ползать муравья, то где бы он ни прополз, нельзя будет сказать, что он пересек границу поверхности.
Само наличие материальной (реально изготовленной) модели односторонней поверхности без края доказывает, что такую модель можно получить в трехмерном пространстве, не выходя для этого в четырехмерное пространство.
Если рассматривать в трехмерном пространстве эту одностороннюю поверхность без края в качестве топологического объекта, то можно утверждать, что она односвязна и не гомеоморфна двумерной сфере. Однако она не нарушает знаменитую гипотезу Пуанкаре, поскольку эта поверхность не является компактным многообразием и вообще не является многообразием.
декабрь 2010 года