| О проекте | Главная | Оставить сообщение | Адрес для связи: tbam1@rambler.ru |

            Традиционно под невозможными фигурами понимаются плоские изображения фигур (треугольника, прямоугольника, тора, куба, спирали и др.), которые невозможно представить в трехмерном виде. Т. е. имеются в виду изображения фигур отображенные исключительно на плоскость. Математические законы получения иллюзий невозможности представления в трехмерном виде тех или иных геометрических фигур (объектов) (а невозможность представления нарисованной на плоскости геометрической фигуры в трехмерном виде, вопреки установившемся представлениям, действительно является лишь иллюзией) приведены в статьях: "Невозможные фигуры – порнография в искусстве. Математическое описание невозможных фигур" http://stob2.narod.ru/9s.htm и "Анимация невозможных объектов (фигур) и возникновение иллюзии их невозможности в трехмерном пространстве" http://stob2.narod.ru/34s.htm .

            Естественно возникает вопрос, а что будет, если изображения различных геометрических фигур (объектов) отображать не на плоскость, а на поверхности многогранников или в частном случае на криволинейные поверхности?

            Здесь криволинейные поверхности рассматриваются в качестве частного случая поверхности или части поверхности многогранника в связи с тем, что любая криволинейная поверхность всегда может быть представлена в виде многогранника и более того даже построена при помощи уравнений, описывающих поверхности многогранников. Так, например, поверхности шара, эллипсоида, тора фактически являются поверхностями многогранников только с очень большим количеством граней – бесконечно большим количеством граней. Об этом подробно можно прочесть в статье: "Многогранник – единая и универсальная геометрическая форма всего" http://stob2.narod.ru/10i.htm .

            Есть еще вопросы с возможностью адекватного отображения плоского изображения на поверхность многогранника. Такое отображение возможно, возможно даже непрерывное такое отображение. Как это достигается можно прочитать в статье: " Неудобные вопросы и парадоксы современной топологии" http://stob2.narod.ru/33s.htm . Конечно, даже при таком отображении деформаций изображений фигур избежать не удастся, но для цели данной статьи это не будет являться существенным.

            Для того чтобы посмотреть, как будут выглядеть изображения геометрических фигур на поверхностях различных многогранников, возьмем изображения сравнительно простых по своей форме геометрических фигур (объектов): обычный треугольник (Рис. 1), этот же треугольник, но представленный, как классический невозможный треугольник (Рис. 2) и обычный прямоугольник (Рис. 3).

Рис. 1 Обычный треугольник

Рис. 2 Невозможный треугольник

Рис. 3 Обычный прямоугольник

            Теперь отобразим их на поверхности различных многогранников и посмотрим, что получилось:

Рис. 4 Обычный треугольник, размещенный на поверхности многогранника с очень большим количеством граней, который принято называть шаром или сферой

Рис. 5 Обычный треугольник, размещенный на поверхности многогранника с очень большим количеством граней, который принято называть шаром или сферой. В отличие от изображения на Рис. 4 половина граней многогранника выполнены в более темном цвете для того, чтобы показать, что это действительно многогранник, а не шар или сфера.

Рис. 6 Невозможный треугольник, размещенный на поверхности многогранника с очень большим количеством граней, который принято называть шаром или сферой

Рис. 7 Обычный треугольник, размещенный на поверхности многогранника с четырнадцатью гранями

Рис. 8 Невозможный треугольник, размещенный на поверхности многогранника с четырнадцатью гранями

Рис. 9 Обычный треугольник, размещенный на поверхности куба

Рис. 10 Невозможный треугольник, размещенный на поверхности куба

Рис. 11 Обычный прямоугольник, размещенный на поверхности многогранника с двадцатью шестью гранями

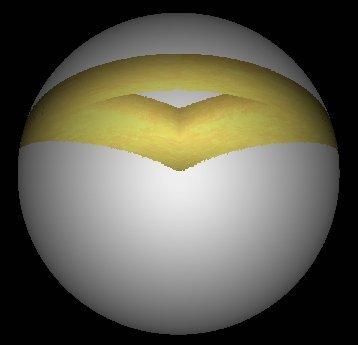
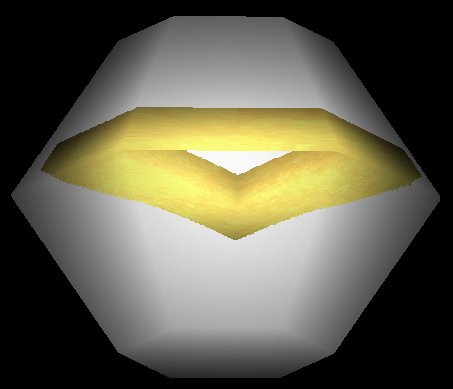
            Подобных изображений можно получить бесконечно много, так как количество различных многогранников и различных геометрических фигур бесконечно. Но уже и представленных выше изображений достаточно для выявления общих их свойств.

            Если для размещения на поверхности многогранника использовалось невозможное изображение геометрической фигуры, то оно само по себе (без учета многогранника) так и сохраняет свою невозможность в трехмерном представлении.

            В совокупности с поверхностью многогранника любая геометрическая фигура (объект), как возможная, так и невозможная становятся невозможными в трехмерном представлении.

            Действительно, для того чтобы представленные на Рис. 4 – 11 геометрические фигуры можно было реально разместить в трехмерном пространстве они должны полностью или хотя бы частично быть помещены во внутрь нарисованных совместно с ними многогранников, что физически выполнить невозможно.

            В ходе отображения изображения геометрической фигуры на поверхность многогранника она испытывает определенные деформации, но эти деформации, как правило, не мешают восприятию невозможности ее размещения на поверхности многогранника. Хотя могут трансформировать одну геометрическую фигуру в другую. Так, например, на Рис. 9-10 изначально изображения треугольников трансформировались в отчетливые изображения четырехугольников.

            Наличие у многогранника отчетливых ребер усиливает эффект невозможности размещения геометрических фигур на его поверхности.

                                                                                                            апрель 2012 года